Gender disparities in rehospitalisations after coronary artery bypass grafting: evidence from a functional causal mediation analysis of the MIMIC-IV data
October 29, 2024
1 Introduction↩︎
Hospital readmissions are a primary target to improve for both policymakers and clinical administrators, as they are expensive to healthcare systems and are an implication of the quality of care [1]–[3]. The total number of rehospitalisations within 30 days in 2020 for patients in the United States is over 3.4 million with an average readmission rate of 14%, imposing a combined annual cost of over $59 billion on all payers. [4]. Moreover, as suggested by [2], the rate of postoperative readmissions is significantly lower in hospitals with high surgical volume and low rates of surgical mortality. The fact that the reduction in readmissions is related to other quality measures of hospital care further reinforces it as a priority for clinical practitioners.
Coronary artery bypass graft (CABG) surgery, a procedure that restores blood flow to the heart by redirecting blood around blocked or narrowed coronary arteries using grafts, accounts for more than half of all adult cardiac surgical procedures [5]. The prevalence of CABG, along with its hefty $13,499 mean cost of readmission [6], make CABG a key focus for reducing healthcare expenses.
Female gender has been consistently reported by existing literature to be a significant risk factor for various postoperative complications following CABG. This raises another concern in addition to healthcare expenditures: the problem of health equity. [7] and [8] find that women tend to suffer more postoperative comorbidities, as well as higher odds of death. Readmissions, as a potential measure of medical care received during the primary hospital stay, further highlight the issue of gender disparities. For over two decades, analyses of readmissions following CABG have persistently revealed that female patients are more likely to be rehospitalised within a short period after discharge [6], [9]–[14]. Attempts to elucidate the underlying mechanisms of such gender differences are of great interest to health research since such understandings prevent adverse decisions based on purely associational conclusions. For example, referrals of women for CABG could be delayed according to such findings [15], which could further undermine the well-being of female patients in need. While more recent studies have begun investigating the specific reasons behind the worse outcomes for women, the area remains largely understudied. Some of the hypotheses made from discoveries by [8] include higher comorbidity burdens, underdiagnosis, undertreatment, delays in treatment, as well as biological differences for female ischemic heart disease patients.
Leveraging the vast amount of data in the Medical Information Mart for Intensive Care IV (MIMIC-IV) database [16], we aim to investigate gender disparities in hospital readmission counts following CABG surgery, with a focus on the mediating role of time-varying central venous pressure during the post-surgical ICU stay through the lens of causal mediation analysis. Central venous pressure (CVP) is a hemodynamic parameter that measures the pressure in the large veins near the heart, indicating blood volume and heart function. Although CVP is regularly measured and documented, its potential as a prognostic indicator of postoperative outcomes in patients following CABG has received insufficient attention [17]. In fact, [17] shows that CVP measured 6 hours post-surgery is associated with operative mortality and renal failure after CABG. Our research question in this paper is two-fold. Firstly, we would like to investigate the causal effect of gender on the number of hospital readmissions within 60 days of discharge from the primary hospital stay among patients who underwent CABG in the MIMIC-IV database. Secondly, we intend to examine whether the time-varying CVP measured over the post-surgical ICU stay mediates the causal pathway from gender to rehospitalisations. Consequently, we arrive at a functional causal mediation analysis with a zero-inflated count outcome, with gender being a binary treatment, time-varying CVP during the postoperative ICU stay being a functional mediator, and the 60-day readmission count as a zero-inflated count outcome.
Applying functional data analysis (FDA) techniques to causal mediation analysis with time-varying mediators commenced fairly recently with the work of [18]. [18] considers a framework where the mediator is a continuous function of time, the treatment assignment is a binary univariate scalar, and the outcome is a continuous univariate scalar. Subsequently, linear functional structural equation models (lfSEM), as a functional analogue to a linear SEM, are proposed to assess mediation. [19] proposes a similar framework to study the effect of varenicline on smoking cessation, mediated by time-varying craving to smoke. A causal mediation framework is introduced to account for a binary treatment comparing varenicline to nicotine replacement therapy, with time-varying smoking cravings, collected via EMA prompts, as a functional mediator, and a distal binary abstinence outcome. The same topic is also explored by [20], accommodating both a functional mediator and a functional outcome by specifying an SEM with functional response regressions. [21] further advances functional causal mediation analysis by addressing sparse and irregular longitudinal data, employing functional principal component analysis (FPCA) and a Bayesian approach to estimate direct and indirect effects, particularly in settings where the mediator and outcome are observed on irregular time grids such as the animal behaviour data studied. [22] develops a framework that combines mediation analysis with Granger causality to capture spatio-temporal dependencies in fMRI time series, providing insights into brain mechanisms. [23], [24] extend the setting further to incorporate functional data in all of the treatment, mediator and outcome. Specifically, they develop two models: the concurrent mediation model, which assumes point-wise relationships at each time point, and the historical mediation model, which accounts for cumulative effects over time. These models allow for the estimation of time-varying direct and indirect effects, making them suitable for applications where functional data is involved with all components of the causal mediation framework. Currently, the scope of this area of study is limited to linear modelling of the mediation framework. Zero-inflated count data, observed in many applications across fields such as healthcare, ecology, and economics, involves count outcomes with an excess of zeros. For instance, the number of hospital readmissions, counts of dental caries where many individuals may have no cavities, the number of substance use relapses where some individuals remain abstinent, and insurance claims where no claims are made during the study period all exhibit this pattern. Causal mediation analysis with zero-inflated count outcomes entails a nonlinear relationship between the treatment, mediator and outcome. Related works have been done in a scalar setting [25], [26]. Non-functional causal mediation analysis with a zero-inflated count outcome typically involves fitting a linear model for the mediator and a zero-inflated count model, such as the zero-inflated Poisson or zero-inflated Negative Binomial models, for the outcome. However, such problems have yet to be examined under scenarios of a functional mediator.
Significant research on nonlinear FDA techniques has emerged in the recent decade [27]. One of the most commonly adopted methods is nonlinear functional regression models. Nonlinear functional regression models extend their linear counterparts by combining a nonlinear link function with linear predictors. With an attempt to model hospitalisations in patients with dialysis, [28] proposes functional linear models for zero-inflated count data. Their work outlined the formulation and estimation of a functional zero-inflated Poisson (ZIP) model with a functional predictor and multiple cross-sectional predictors to model counts generated by a mixture distribution.
Motivated by the research question, we extend existing causal mediation methodologies by introducing a framework that incorporates both a functional mediator and a zero-inflated count outcome. The potential outcomes framework [29] is employed to define the causal effects of interest in this context and provide the theoretical underpinning for our approach, including conditions for effect identification. To address both the time-varying nature of the mediator and the zero-inflated count outcomes, functional linear and nonlinear models are implemented. Estimation and inference on the direct and indirect effects are performed by a parameter-simulating quasi-Bayesian Monte Carlo approximation method based on the mediation formula [30]. Simulation studies validate our approach, demonstrating its capability to estimate causal effects reliably in this context. Using the method proposed, we find both a significant total effect of gender on rehospitalisation counts and a significant natural indirect effect channelled through time-varying CVP.
In this paper, we start by introducing the causal mediation analysis with a functional mediator and a zero-inflated count outcome using the potential outcomes framework in Section 2. We define the causal total effect, natural direct effect, and natural indirect effect, as well as present assumptions for identification and nonparametric identification of the causal effects. In Section 3, we demonstrate the proposed methods, including the mediator model, the outcome model, and a parameter-simulating quasi-Bayesian Monte Carlo approximation algorithm. The performances of the proposed method are assessed via simulation studies in Section 4. Section 5 describes the data selected from MIMIC-IV and discusses findings regarding our research question. Section 6 concludes the paper by giving a discussion.
2 Functional causal mediation analysis with a zero-inflated outcome↩︎

Figure 1: A causal diagram for a causal mediation analysis with a functional mediator.
As illustrated in Figure 1, the causal mediation analysis of interest involves a binary treatment \(A\), a zero-inflated count outcome \(Y\), a \(p\)-dimensional vector of baseline covariates \(\mathbf{X}\), and a time-varying mediator \(M(t)\) as a function of time. Notice that the time \(t\) is rescaled so that \(t \in [0,1]\). We explore a study with a sample of \(n\) individuals, where each pertains to either the treatment group with \(A_i=1\), or the control group with \(A_i=0\), for \(i=1,\ldots,n\). The functional mediator \(M(t)\) is a function of time and is therefore a smooth stochastic process. For each individual \(i\), discrete observations \(M_{ij}\) of the mediator occur at \(T\) regularly spaced time points \(t_j\) with \(j=1,\ldots,T\), and are regarded as realisations of the underlying smooth process. The underlying smooth process \(M(t)\) can be constructed as a functional data object from the discrete observations using a variety of methods [31]. The end-point outcome \(Y_i\) is measured at the end of the study. The baseline covariates \(\mathbf{X}\) include variables that confound the relation between \(A\) and \(Y\), the relation between \(M(t)\) and \(Y\), or the relation between \(A\) and \(M(t)\), and are not affected by \(A\). Both the treatment assignment and baseline covariate measurement take place at the beginning of the study.
The causal estimands are defined in Section 2.1 followed by a discussion on the relevant identifying assumptions in Section 2.2. In 2.3, we present nonparametric identification results of the causal effects.
2.1 Definition of causal effects↩︎
In defining the causal effects of interest, we introduce the potential outcomes framework in the context of mediation analysis [32] with a functional mediator. To accommodate the functional mediator, the bold font notation \(\mathbf{M} = \{M(t) \mid t \in [0,1]\}\) is used to denote the mediator process over the entire time range. It is worth pointing out that \(\mathbf{M}\) has realisations as sample paths \(\mathbf{m} \in \mathcal{D}_\mathbf{M}^{[0,1]}\), where \(\mathcal{D}_\mathbf{M}^{[0,1]} \subseteq \mathbb{R}^{[0,1]}\) refers to the range of the mediator process and contains real-valued functions defined on the interval \([0,1]\). We can consequently write \(\mathbf{M}_i(a)\), for \(a = 0, 1\), as the potential values of the underlying mediator process over the entire time range for individual \(i\) under treatment level \(a\). \(Y_i(a, \mathbf{M}_i(a^\prime))\) then refers to the potential value of the outcome \(Y\) for individual \(i\) if, potentially counterfactually, the individual received treatment \(a\) and had values of the mediator process at the level that would have been observed under treatment \(a^\prime\).
We can then define the total effect (TE) of the treatment \(A\) on the outcome \(Y\) as \[\tau_{\textsubscript{TE}} \equiv E\left\{Y\left(1, \mathbf{M}(1)\right) - Y\left(0, \mathbf{M}(0)\right)\right\}.\label{eq:totaleffect}\tag{1}\] The total effect is defined as the mean difference in potential outcomes under treatment levels 1 and 0. [33] proposes a framework for decomposing the total effect (TE) into direct and indirect effects in the presence of a mediator. We build upon this framework by extending it to accommodate a functional mediator, allowing for definitions of the natural direct and indirect effects in our settings. In particular, the natural indirect effect (NIE) is defined as the mean difference in the potential outcomes under a fixed treatment level but varied potential values of the mediator process under different treatment levels, \[\tau_{\textsubscript{NIE}}(a) \equiv E\left\{Y\left(a, \mathbf{M}(1)\right) - Y\left(a, \mathbf{M}(0)\right)\right\}, \quad a=0,1.\label{eq:nie}\tag{2}\] The NIE measures the component of the treatment’s causal effect on the outcome channelled through the mediator. Similarly, the natural direct effect (NDE) is the effect that does not go through the mediator and is defined as the mean difference in the potential outcomes under different treatment values and the potential values of the mediator process at a fixed treatment level, \[\tau_{\textsubscript{NDE}}(a) \equiv E\left\{Y\left(1, \mathbf{M}(a)\right) - Y\left(0, \mathbf{M}(a)\right)\right\}, \quad a=0,1.\label{eq:nde}\tag{3}\] The decomposition of TE can be straightforwardly confirmed as NIE and NDE sum to TE, \[\tau_{\textsubscript{TE}} = \tau_{\textsubscript{NIE}}(a) + \tau_{\textsubscript{NDE}}(1-a), \quad a=0,1.\]
The definitions of the causal estimands of interest require comparing four potential outcomes: \(Y\left(1, \mathbf{M}(1)\right)\), \(Y\left(1, \mathbf{M}(0)\right)\), \(Y\left(0, \mathbf{M}(1)\right)\), and \(Y\left(0, \mathbf{M}(0)\right)\). However, in practice, only one of these potential outcomes can be observed, which is also known as the fundamental problem of causal inference [34]. As a result, certain assumptions are needed in order to identify the potential outcomes from the observed data.
2.2 Identifying assumptions↩︎
The assumptions of identification for causal mediation analysis have been intensively discussed [33], [35]–[39]. However, such assumptions involving a functional mediator need further clarification. Following the guidance of [39] and [24], we examine and outline the identifying assumptions for causal mediation analysis with a functional mediator.
Assumption 1 (Positivity). For \(a \in \left\{0, 1\right\}\), \(P(A = a \mid \mathbf{X}) > 0\); for any Borel measurable set \(\mathcal{B} \subseteq \mathcal{D}_\mathbf{M}^{[0,1]}\) that has positive measures, the probability that a sample path \(\mathbf{m}\) of the process \(\mathbf{M}\) belongs to \(\mathcal{B}\) given \(\mathbf{X}\) and \(A = a\) is positive: \(P(\mathbf{m} \in \mathcal{B} \mid \mathbf{X}, A = a) > 0\).
Assumption 2 (Consistency of the potential outcome). Given any Borel measurable set \(\mathcal{B} \subseteq \mathcal{D}_\mathbf{M}^{[0,1]}\) that has positive measures, for all \(\mathbf{m} \in \mathcal{B}\) and \(a \in \left\{0, 1\right\}\), if \(A = a\) and \(\mathbf{M} = \mathbf{m}\), \[Y = Y(a, \mathbf{m}).\] Namely, the observed outcome reveals the potential outcome under the respective treatment level and mediator process.
Assumption 3 (Consistency of the potential mediator). For \(a \in \left\{0, 1\right\}\), if \(A = a\), \[\mathbf{M} = \mathbf{M}(a).\] Namely, the observed mediator process reveals the potential mediator process under the respective treatment level.
Assumption 4 (Consistency of the cross-world potential outcome). Given any Borel measurable set \(\mathcal{B} \subseteq \mathcal{D}_\mathbf{M}^{[0,1]}\) that has positive measures, for all \(\mathbf{m} \in \mathcal{B}\) and \(a, a^\prime \in \left\{0, 1\right\}\), if \(\mathbf{M}(a^\prime) = \mathbf{m}\), \[Y(a, \mathbf{m}) = Y(a, \mathbf{M}(a^\prime)).\] Namely, the potential outcome reveals the cross-world potential outcome under the respective potential mediator process.
Assumption 5 (Conditional independence). Given any Borel measurable set \(\mathcal{B} \subseteq \mathcal{D}_\mathbf{M}^{[0,1]}\) that has positive measures, for all \(\mathbf{m} \in \mathcal{B}\) and \(a, a^\prime \in \left\{0, 1\right\}\), \[\begin{align} \left\{Y(a^\prime , \mathbf{m}), \mathbf{M}(a)\right\} \perp\!\!\!\!\perp A &\mid \mathbf{X},\\ Y(a^\prime , \mathbf{m}) \perp\!\!\!\!\perp\mathbf{M}(a) &\mid \mathbf{X}, A = a. \end{align}\] Namely, given the observed baseline covariates, the treatment is unconfounded for the potential outcomes and potential mediator processes, and the mediator process is unconfounded for the potential outcomes.
2.3 Nonparametric identification of the causal effects↩︎
Under the previously discussed identifying assumptions, the causal effects in a causal mediation analysis involving a functional mediator can be nonparametrically identified from the observed data distribution. Specifically, \[\begin{align} \tau_{\textsubscript{NIE}}(a) &= E_{\mathbf{X}}\left\{E\left(Y \mid A=a, \mathbf{X}\right) \right\} - E_{\mathbf{X}}\left[E_{\mathbf{M} \mid A = a^\prime, \mathbf{X}} \left\{E\left(Y \mid A = a, \mathbf{M}, \mathbf{X}\right)\right\}\right],\\ \tau_{\textsubscript{NDE}}(a^\prime) &= E_{\mathbf{X}}\left[E_{\mathbf{M} \mid A = a^\prime, \mathbf{X}} \left\{E\left(Y \mid A = a, \mathbf{M}, \mathbf{X}\right)\right\}\right] - E_{\mathbf{X}}\left\{E\left(Y \mid A=a^\prime, \mathbf{X}\right) \right\}, \\ \tau_{\textsubscript{TE}} &= E_{\mathbf{X}}\left\{E\left(Y \mid A=a, \mathbf{X}\right) \right\} - E_{\mathbf{X}}\left\{E\left(Y \mid A=a^\prime, \mathbf{X}\right) \right\}. \end{align}\] Consequently, to estimate the causal effects, the nonparametric identification results require modelling: (a) the observed outcome \(Y\) conditional on the observed treatment \(A\), mediator process \(\mathbf{M}\) and baseline covariates \(\mathbf{X}\); (b) the observed mediator process \(\mathbf{M}\) conditional on the observed treatment \(A\) and baseline covariates \(\mathbf{X}\).
3 Methods proposed↩︎
Without the presence of functional data and nonlinearity, the models mentioned in Section 2.3 correspond to the linear structural equation models (SEM) used in traditional mediation analysis [40]. Causal mediation analysis, by defining the causal effects using the potential outcomes frameworks, enables the use of more complex statistical models to accommodate a functional mediator and a zero-inflated count outcome. We describe a function-on-scalar regression for the functional mediator and its estimation in Section 3.1. Section 3.2 presents a functional zero-inflated Poisson (ZIP) model for the outcome. Finally, we propose a parameter-simulating quasi-Bayesian Monte Carlo approximation method to perform estimation and inference for the causal effects in Section 3.3.
3.1 A function-on-scalar regression mediator model↩︎
3.1.1 Model formulation↩︎
As previously discussed, the discrete measurements of CVP during the post-surgical ICU stay are regarded as observations of an underlying smooth CVP process, which can be seen as a function of time. We thus propose to model the functional mediator with a function-on-scalar regression [41]. Specifically, it is assumed that the functional mediator \(M(t)\) follows a function-on-scalar regression on both the treatment \(A\) and the baseline covariates \(\mathbf{X}\), \[\label{eq:mediatormodel} M_{i}(t) = \beta_{0}(t) + \beta_{1}(t)A_i + \mathbf{X}^\mathsf{T}_i\boldsymbol{\beta}_{2}(t) + \varepsilon_{i}(t), \quad \text{for} \quad t \in [0,1],\tag{4}\] where \(\boldsymbol{\beta}_{2}(t) = \left[\beta_{21}(t), \beta_{22}(t), \ldots, \beta_{2p}(t)\right]^\mathsf{T}\) is a \(p\)-dimensional vector of functions. The intercept function is \(\beta_0(t)\), the functional coefficients \(\beta_{1}(t)\) and \(\boldsymbol{\beta}_{2}(t)\) represent the partial effects of \(A\) and \(\mathbf{X}\) on the mediator \(M(t)\) at time \(t\), and \(\varepsilon_{i}(t)\) is a random error process. The random error process \(\varepsilon_{i}(t)\) is assumed to be a Gaussian process with mean zero.
3.1.2 Procedures for estimation↩︎
The least squares method after basis expansion is used to estimate the functional parameters. Basis functions can be derived from Fourier analysis, splines, or functional principal component analysis (FPCA) [41], [42]. The selection of the basis system can be made in several ways. First, the standard practice is to determine, based on the nature and shape of the functional mediator, the set of basis functions used to describe the functional mediator and use the same basis system for all coefficient functions. Another plausible approach is to determine a different basis system for each coefficient function with prior background knowledge. For example, we may be aware that the effect of the covariate \(\mathbf{X}\) on the functional mediator does not change over time, and therefore specify a constant basis for the respective coefficient function. Moreover, the choice of basis functions can also be made according to empirical testing. For example, models with different specifications of basis systems can be fitted and compared via criteria such as the generalised cross-validation measure and cross-validation score [41].
After deciding on a set of basis functions \(\left\{\phi_1(t), \cdots, \phi_K(t)\right\}\), the coefficient functions can be expanded with the basis functions as \[\begin{align} \beta_0(t)&=\sum_{k=1}^K b_{0 k} \phi_k(t), \\ \beta_1(t)&=\sum_{k=1}^K b_{1 k} \phi_k(t), \\ \boldsymbol{\beta}_2(t) &= \sum_{k=1}^K \mathbf{b}_{2 k} \phi_k(t), \end{align}\] where \(\mathbf{b}_{2 k} = \left[b_{21 k}, b_{22 k}, \ldots, b_{2p k}\right]^\mathsf{T}\). Model (4 ) can then be written as \[\label{eq:reducedmediatormodel} M_i(t) = \sum_{k=1}^Kb_{0k}\phi_k(t) + A_i\sum_{k=1}^Kb_{1k}\phi_k(t) + \mathbf{X}^\mathsf{T}_i \left(\sum_{k=1}^K \mathbf{b}_{2 k} \phi_k(t) \right) + \varepsilon_i(t),\tag{5}\] thereby reducing the problem to estimating the basis coefficients \(\{b_{0k}, b_{1k}, \mathbf{b}_{2k} \}_{k = 1, \ldots, K}.\) Under the assumption of full and regular observation on the grid \(\{t_1, \ldots, t_T\}\) of the mediator functions \(M_i\), Model (5 ) can be expressed in a matrix format, \[\label{eq:mediatormodelmatrix} \mathcal{M}=\mathbf{Z} \mathbf{B}\boldsymbol{\Phi}^\mathsf{T}+\mathbf{E},\tag{6}\] where \[\begin{align} \mathcal{M}&=\left[\begin{array}{ccccc} M_1(t_1) & M_1(t_2) & \ldots & M_1(t_T) \\ M_2(t_1) & M_2(t_2) & \ldots & M_2(t_T) \\ \vdots & \vdots & \vdots & \vdots\\ M_n(t_1) & M_n(t_2) & \ldots & M_n(t_T) \\ \end{array}\right], \mathbf{Z}=\left[\begin{array}{cccc} 1 & A_1 & \mathbf{X}^\mathsf{T}_1 \\ 1 & A_2 & \mathbf{X}^\mathsf{T}_2 \\ \vdots & \vdots & \vdots \\ 1 & A_n & \mathbf{X}^\mathsf{T}_n \end{array}\right], \mathbf{B}=\left[\begin{array}{ccc} b_{01} & \ldots & b_{0K} \\ b_{11} & \ldots & b_{1K} \\ b_{211} & \ldots & b_{21K} \\ \vdots & \vdots & \vdots \\ b_{2p1} & \ldots & b_{2pK} \\ \end{array}\right], \\ \boldsymbol{\Phi}&=\left[\begin{array}{ccc} \phi_1(t_1) & \ldots & \phi_K(t_1) \\ \phi_1(t_2) & \ldots & \phi_K(t_2) \\ \vdots & \vdots & \vdots \\ \phi_1(t_T) & \ldots & \phi_K(t_T) \\ \end{array}\right], \mathbf{E}=\left[\begin{array}{ccc} \varepsilon_1(t_1) & \ldots & \varepsilon_1(t_T) \\ \varepsilon_2(t_1) & \ldots & \varepsilon_2(t_T) \\ \vdots & \vdots & \vdots \\ \varepsilon_n(t_1) & \ldots & \varepsilon_n(t_T) \\ \end{array}\right]. \end{align}\] In other words, \(\mathcal{M}\) is an \(n \times T\) matrix whose rows consist of discrete observations of the functional mediator for each individual, \(\mathbf{Z}\) is the design matrix of the regression, \(\mathbf{B}\) is a \((p+2) \times K\) matrix whose rows consist of basis coefficients corresponding to the respective coefficient functions, \(\boldsymbol{\Phi}\) is a \(T \times K\) matrix whose rows consist of basis functions evaluated at each of the \(T\) discrete time points, and \(\mathbf{E}\) is an \(n \times T\) matrix containing vector-valued error functions.
For ordinary least squares estimation, the rows of \(\mathcal{M}\), \(\mathbf{Z}\mathbf{B}\boldsymbol{\Phi}^\mathsf{T}\), and \(\mathbf{E}\) are concatenated to form \(\operatorname{vec}(\mathcal{M}^\mathsf{T})\), \(\operatorname{vec}((\mathbf{Z}\mathbf{B}\boldsymbol{\Phi}^\mathsf{T})^\mathsf{T})\), and \(\operatorname{vec}(\mathbf{E}^\mathsf{T})\). Also, note that \(\operatorname{vec}((\mathbf{Z}\mathbf{B}\boldsymbol{\Phi}^\mathsf{T})^\mathsf{T}) = (\mathbf{Z} \otimes \boldsymbol{\Phi}) \operatorname{vec}(\mathbf{B}^\mathsf{T})\), where \(\otimes\) represents the Kronecker product. Model (6 ) can then be transformed into a standard linear model as \[\label{eq:mediatormodelvector} \operatorname{vec}\left(\mathcal{M}^\mathsf{T}\right)=(\mathbf{Z} \otimes \boldsymbol{\Phi}) \operatorname{vec}\left(\mathbf{B}^\mathsf{T}\right)+\operatorname{vec}(\mathbf{E}^\mathsf{T}).\tag{7}\] This way, \(\operatorname{vec}\left(\mathbf{B}^\mathsf{T}\right)\) can be estimated by ordinary least squares and \(\widehat{\mathbf{B}}\) can be obtained by rearranging \(\operatorname{vec}\left(\widehat{\mathbf{B}}^\mathsf{T}\right)\).
3.2 A functional zero-inflated Poisson outcome model↩︎
3.2.1 Model formulation↩︎
While most existing literature on rehospitalisation focuses on the rate of hospital readmissions, our study examines the number of readmissions within 60 days following discharge from the primary CABG hospital stay. This outcome provides deeper insights, albeit posing greater modelling challenges due to zero-inflation. The zero-inflated Poisson (ZIP) model, proposed by [43], models count data with excessive zero-valued observations by considering a mixture of a binary model for generating zeros and a standard Poisson model for generating non-zero counts, as well as some zeros. Zeros produced by the former are often referred to as “structural zeros” or “excess zeros” since the process cannot generate any counts other than zero. [28] later extended it to a functional version, with which we can parameterise the ZIP model with functional covariates. We assume that the end-point outcome \(Y\) follows a functional ZIP model, \[\label{eq:outcomemodel} P(Y_i = y_i | \mathbf{M}_i, A_i, \mathbf{X}_i) = \begin{cases} p_i + (1 - p_i)e^{-\lambda_i}, & \text{if } y_i = 0 \\ (1 - p_i) \frac{e^{-\lambda_i} \lambda_i^{y_i}}{y_i!}, & \text{if } y_i > 0 \end{cases},\tag{8}\] where \(p_i\) and \(\lambda_i\) are related to the functional mediator, the treatment, and the baseline covariates through some link functions. Here we consider a logit link function for \(p_i\) and a log link function for \(\lambda_i\) where \[\begin{align} \log\frac{p_i}{1-p_i} &= \alpha_0 + \int_0^1 \alpha_1(t)M_i(t) \, dt + \alpha_2A_i + \mathbf{X}_i^\mathsf{T}\boldsymbol{\alpha}_3, \tag{9}\\ \log\lambda_i &= \gamma_0 + \int_0^1 \gamma_1(t)M_i(t) \, dt + \gamma_2A_i + \mathbf{X}_i^\mathsf{T} \boldsymbol{\gamma}_3. \tag{10} \end{align}\] The individual end-point outcome \(Y_i\) is either an excess zero, which takes the value of zero from a Bernoulli distribution with probability \(p_i\), or a zero from a Poisson distribution that has mean \(\lambda_i\) with probability \(1-p_i\).
3.2.2 Procedures for estimation↩︎
Estimation of Model (8 ) requires estimating the parameters in the log-linear model for \(\lambda_i\) and the logistic model for \(p_i\). The problem is thus to estimate the scalar-on-function models for \(\log(\frac{p_i}{1-p_i})\) and \(\log\lambda_i\). To transform the scalar-on-function models into standard linear models, we use techniques from functional principal components regression (FPCR) to expand the functional mediator \(M(t)\) and the coefficient functions \(\alpha_1(t)\), \(\gamma_1(t)\) into functional principle components (FPCs) of \(M(t)\) [42]. The resulting parameters are then estimated by maximum likelihood.
We assume the functional mediator admits the Karhunen–Loéve expansion as the following, \[M(t)=\mu(t)+\sum_{j=1}^{\infty} \xi_j v_j(t),\] where \(\mu(t)=E\left(M(t)\right)\) is the mean function of the functional mediator, \(v_1, v_2, \ldots\) are a set of orthonormal eigenfunctions, and \(\xi_j\) are the scores. Given \(\left\{M_i(t), i=1, \ldots, n\right\}\), FPCR reduces the scalar-on-function models for \(\log(\frac{p_i}{1-p_i})\) and \(\log\lambda_i\) to standard linear models by approximating the functional mediator with an estimated mean function and \(q\) estimated functional principal components, \[M_i(t) \approx \widehat{\mu}(t)+\sum_{j=1}^q \widehat{\xi}_{i j} \widehat{v}_j(t),\] where \(\widehat{\mu}(t)=\frac{1}{n} \sum_{i=1}^n M_i(t)\) is the estimated mean function, \(\widehat{v}_j(t)\) are the estimated eigenfunctions, and \(\widehat{\xi}_{i j}=\int_0^1 \left[M_i(t)-\widehat{\mu}(t)\right] \widehat{v}_j(t) d t\) are the estimated scores. Consequently, Models (9 ) and (10 ) can be written as \[\begin{align} \log\frac{p_i}{1-p_i} & \approx \alpha^*_0+\sum_{j=1}^q \widehat{\xi}_{i j} \alpha^*_j+\alpha_2A_i + \mathbf{X}^\mathsf{T}_i\boldsymbol{\alpha}_3 \tag{11}\\ \log\lambda_i & \approx \gamma^*_0+\sum_{j=1}^q \widehat{\xi}_{i j} \gamma^*_j+\gamma_2A_i + \mathbf{X}^\mathsf{T}_i\boldsymbol{\gamma}_3, \tag{12} \end{align}\] where \[\begin{align} &\alpha^*_0=\alpha_0+\int_0^1 \alpha_1(t) \widehat{\mu}(t) d t, \quad \alpha^*_j=\int_0^1 \alpha_1(t) \widehat{v}_j(t) d t \quad \text{ and } \\ &\gamma^*_0=\gamma_0+\int_0^1 \gamma_1(t) \widehat{\mu}(t) d t, \quad \gamma^*_j=\int_0^1 \gamma_1(t) \widehat{v}_j(t) d t. \end{align}\] The choice of the number of estimated functional principal components of \(M_i(t)\) to be used is important. We opt to approximate the mediator function \(M_i(t)\) with the first \(q\) estimated principal components with at least 90% variance explained [44].
The parameters \(\boldsymbol{\alpha} = (\alpha^*_0, \alpha^*_1, \ldots, \alpha^*_q, \alpha_2, \boldsymbol{\alpha}^\mathsf{T}_3)^\mathsf{T}\) and \(\boldsymbol{\gamma} = (\gamma^*_0, \gamma^*_1, \ldots, \gamma^*_q, \gamma_2, \boldsymbol{\gamma}^\mathsf{T}_3)^\mathsf{T}\) from Models (11 ) and (12 ) can then be estimated by maximising the log-likelihood \[\begin{align} \ell\left(\boldsymbol{\alpha}, \boldsymbol{\gamma}\right)=& \sum_{Y_i=0} \log \left[p_i\left(\boldsymbol{\alpha}\right) +\left\{1-p_i\left(\boldsymbol{\alpha}\right)\right\}e^{-\lambda_i\left(\boldsymbol{\gamma}\right)}\right] \nonumber \\ & +\sum_{Y_i>0}\left[\log \left\{1 - p_i\left(\boldsymbol{\alpha}\right)\right\}-\lambda_i\left(\boldsymbol{\gamma}\right) +Y_i \log \left\{\lambda_i\left(\boldsymbol{\gamma}\right)\right\}-\log \left(Y_{i} !\right)\right]. \end{align}\]
3.3 A parameter-simulating quasi-Bayesian Monte Carlo approximation method↩︎
Having obtained the estimated parameters and estimated variance-covariance matrix of the mediator and outcome models, we propose a parameter-simulating quasi-Bayesian Monte Carlo approximation method to estimate and make inference on the causal effects. The Monte Carlo algorithm by [45] is extended to incorporate a functional mediator. Denote the estimated basis coefficients from the mediator model as \(\widehat{\boldsymbol{\theta}}_\mathbf{M} = \left(\widehat{b}_{0k}, \widehat{b}_{1k}, \widehat{\mathbf{b}}_{2k}\right)_{k = 1, \ldots, K}^\mathsf{T}\), and the estimated variance-covariance matrix for the estimated basis coefficients as \(\widehat{\boldsymbol{\Sigma}}_\mathbf{M}\). Likewise, the estimated parameters of the outcome model are denoted as \(\widehat{\boldsymbol{\theta}}_Y = \left(\widehat{\boldsymbol{\alpha}}^\mathsf{T}, \widehat{\boldsymbol{\gamma}}^\mathsf{T}\right)^\mathsf{T}\), and the estimated variance-covariance matrix for the estimated parameters is denoted as \(\widehat{\boldsymbol{\Sigma}}_Y\). Specifically, we repeatedly simulate \(J\) sets of model parameters from the respective asymptotic sampling distributions of the mediator and outcome models, impute the potential outcomes to calculate the causal effects in each of the \(J\) simulated samples, and take the sample medians of the \(J\) copies of causal effects as point estimates. Algorithm 2 outlines the detailed procedures.
Figure 2: Parameter-based Monte Carlo Simulation of the Causal Effects
4 Simulation Study↩︎
In this section, we assess the performance of the proposed approach on simulated datasets. Procedures for generating data are presented in Section 4.1, followed by a discussion of empirical results from the simulation study, as well as comparisons of the proposed methods to an existing one in Section 4.2.
4.1 Data generation↩︎
We consider the time interval \(\mathcal{T} = [0, 1]\) and evaluate two sample sizes, \(n = 100\) and \(n = 1000\), as well as two observation counts, \(T = 20\) and \(T = 100\), for the functional mediator \(M(t)\) over this interval. Additionally, we explore two different forms of the functional mediator \(M(t)\) as shown in Figure 3, resulting in a total of eight scenarios. For each scenario, we generate \(R = 1000\) replicated datasets corresponding to the specified sample size (\(n = 100\) or \(n = 1000\)).
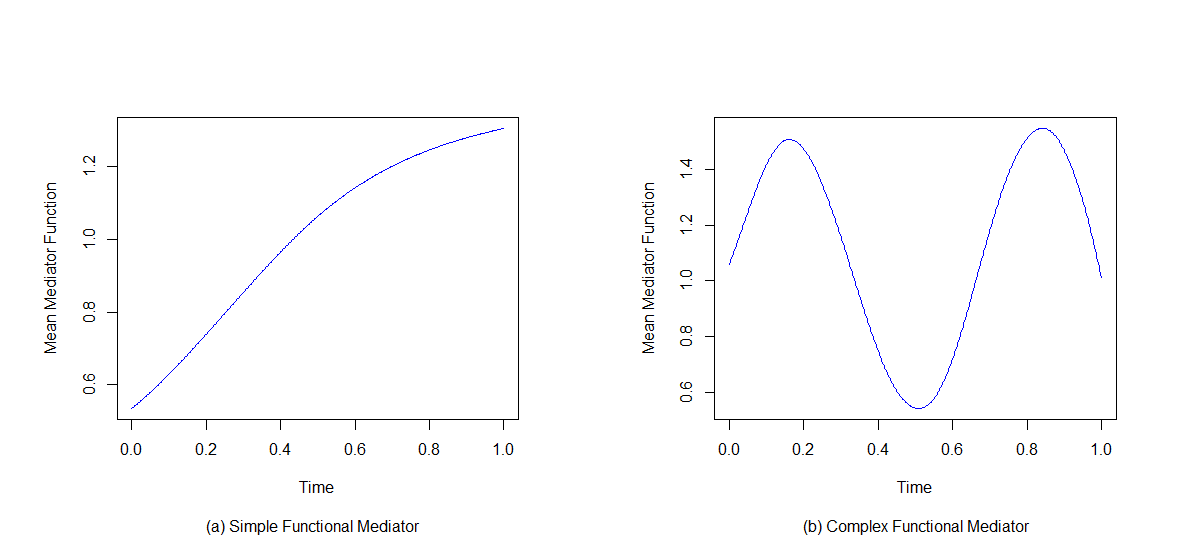
Figure 3: Mean functions of the functional mediator from a \(n = 1000\) generated sample: a simple functional mediator (left panel), a complex functional mediator (right panel).
In each replication dataset, the binary treatment \(A_i\) is assigned randomly with a probability of \(0.5\) to either the treatment or control group. The baseline covariate \(X_i\) is drawn from \(N(1, 3)\). The functional mediator is generated on an evenly spaced grid of 100 or 20 time points over the time interval \(\mathcal{T} = [0, 1]\) as \[M_{i}(t) = \beta_{0}(t) + \beta_{1}(t)A_i + \beta_{2}(t) X_i + \varepsilon_{i}(t).\] For scenarios with a simple functional mediator, \(\beta_{0}(t) = 0\), \(\beta_{1}(t) = 1.5\sin(0.5\pi t)\), \(\beta_{2}(t) = 0.5\). The error term \(\varepsilon_{i}(t)\) is generated from a multivariate normal distribution with mean zero and covariance \(\Sigma(s, t)\), where \(\Sigma(s, t) = \exp(-3|s - t|)\). For scenarios with a complex functional mediator, \(\beta_{0}(t) = 0\), \(\beta_{1}(t) = \sin(3 \pi t) + 1\), \(\beta_{2}(t) = 0.5\). The error term \(\varepsilon_{i}(t)\) is generated from a multivariate normal distribution with mean zero and covariance \(\Sigma(s, t)\), where \(\Sigma(s, t) = 2\exp(-3|s - t|)\). The parameter values are chosen so that the true effect sizes are close among scenarios. Figure 3 illustrates the shapes of a simple functional mediator and a complex one, where the simple mediator function is monotonically increasing on the time interval and the complex mediator function fluctuates as time progresses.
The end-point zero-inflated count outcome \(Y_i\) is generated as \[P(Y_i = y_i | M_{i}(t), A_i, X_i) = \begin{cases} p_i + (1 - p_i)e^{-\lambda_i}, & \text{if } y_i = 0 \\ (1 - p_i) \frac{e^{-\lambda_i} \lambda_i^{y_i}}{y_i!}, & \text{if } y_i > 0 \end{cases},\] where \[\begin{align} \log\frac{p_i}{1-p_i} &= \alpha_0 + \int_0^1 \alpha_1(t)M_i(t) \, dt + \alpha_2A_i + \alpha_3X_i,\\ \log\lambda_i &= \gamma_0 + \int_0^1 \gamma_1(t)M_i(t) \, dt + \gamma_2A_i + \gamma_3X_i. \end{align}\] For scenarios with a simple functional mediator, \(\alpha_{0} = -3\), \(\alpha_{1}(t) = -4(t - 0.5)^2 + 1\), \(\alpha_{2} = 0.5\), \(\alpha_{3} = 0.5\), and \(\gamma_0 = 1\), \(\gamma_1(t) = 0.5\), \(\gamma_2 = 1\), \(\gamma_3 = -0.1\). For scenarios with a complex functional mediator, \(\alpha_{0} = -3.5\), \(\alpha_{1}(t) = 0.07\sin(3 \pi t) + 1\), \(\alpha_{2} = 0.5\), \(\alpha_{3} = 0.5\), and \(\gamma_0 = 1\), \(\gamma_1(t) = 0.5\), \(\gamma_2 = 1\), \(\gamma_3 = -0.1\). The parameter values are chosen so that there are approximately \(35\%\) of the count outcomes in each dataset is zero and that the true effect sizes are close among scenarios.
The true causal direct, indirect and total effects for each scenario are empirically computed by generating a dataset containing \(100,000\) subjects.
4.2 Empirical results↩︎
| True Value | BIAS (%) | ASE | ESE | ECP (%) | |
|---|---|---|---|---|---|
| \(n = 1000\), \(T = 100\) | |||||
| \(\tau_{\textsubscript{TE}}\) | \(5.28\) | \(1.15\) | \(0.314\) | \(0.326\) | \(93.0\) |
| \(\tau_{\textsubscript{NIE}}(1)\) | \(2.02\) | \(1.11\) | \(0.283\) | \(0.289\) | \(93.6\) |
| \(\tau_{\textsubscript{NDE}}(0)\) | \(3.26\) | \(1.26\) | \(0.327\) | \(0.324\) | \(94.1\) |
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.90\) | \(1.97\) | \(0.158\) | \(0.157\) | \(94.7\) |
| \(\tau_{\textsubscript{NDE}}(1)\) | \(4.38\) | \(1.03\) | \(0.358\) | \(0.359\) | \(94.6\) |
| \(n = 100\), \(T = 100\) | |||||
| \(\tau_{\textsubscript{TE}}\) | \(5.28\) | \(1.34\) | \(1.034\) | \(1.045\) | \(94.4\) |
| \(\tau_{\textsubscript{NIE}}(1)\) | \(2.02\) | \(1.51\) | \(1.040\) | \(0.995\) | \(95.8\) |
| \(\tau_{\textsubscript{NDE}}(0)\) | \(3.26\) | \(1.90\) | \(1.131\) | \(1.137\) | \(95.0\) |
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.90\) | \(2.76\) | \(0.581\) | \(0.568\) | \(94.2\) |
| \(\tau_{\textsubscript{NDE}}(1)\) | \(4.38\) | \(1.42\) | \(1.199\) | \(1.209\) | \(95.2\) |
| \(n = 1000\), \(T = 20\) | |||||
| \(\tau_{\textsubscript{TE}}\) | \(5.42\) | \(1.24\) | \(0.326\) | \(0.330\) | \(94.6\) |
| \(\tau_{\textsubscript{NIE}}(1)\) | \(2.14\) | \(2.52\) | \(0.290\) | \(0.293\) | \(94.7\) |
| \(\tau_{\textsubscript{NDE}}(0)\) | \(3.28\) | \(0.49\) | \(0.334\) | \(0.331\) | \(95.7\) |
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.95\) | \(3.32\) | \(0.162\) | \(0.163\) | \(94.8\) |
| \(\tau_{\textsubscript{NDE}}(1)\) | \(4.47\) | \(0.84\) | \(0.371\) | \(0.370\) | \(94.6\) |
| \(n = 100\), \(T = 20\) | |||||
| \(\tau_{\textsubscript{TE}}\) | \(5.42\) | \(1.48\) | \(1.074\) | \(1.078\) | \(94.2\) |
| \(\tau_{\textsubscript{NIE}}(1)\) | \(2.14\) | \(2.00\) | \(1.044\) | \(1.044\) | \(94.9\) |
| \(\tau_{\textsubscript{NDE}}(0)\) | \(3.28\) | \(1.76\) | \(1.139\) | \(1.152\) | \(95.2\) |
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.95\) | \(3.48\) | \(0.586\) | \(0.587\) | \(95.3\) |
| \(\tau_{\textsubscript{NDE}}(1)\) | \(4.47\) | \(1.41\) | \(1.241\) | \(1.228\) | \(95.6\) |
| True value | BIAS (%) | ASE | ESE | ECP (%) | |
|---|---|---|---|---|---|
| \(n = 1000\), \(T = 100\) | |||||
| \(\tau_{\textsubscript{TE}}\) | \(5.20\) | \(1.32\) | \(0.326\) | \(0.343\) | \(92.7\) |
| \(\tau_{\textsubscript{NIE}}(1)\) | \(1.93\) | \(5.68\) | \(0.334\) | \(0.351\) | \(91.2\) |
| \(\tau_{\textsubscript{NDE}}(0)\) | \(3.27\) | \(1.30\) | \(0.354\) | \(0.364\) | \(94.1\) |
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.88\) | \(4.39\) | \(0.203\) | \(0.208\) | \(93.5\) |
| \(\tau_{\textsubscript{NDE}}(1)\) | \(4.32\) | \(0.65\) | \(0.388\) | \(0.395\) | \(93.7\) |
| \(n = 100\), \(T = 100\) | |||||
| \(\tau_{\textsubscript{TE}}\) | \(5.20\) | \(1.21\) | \(1.111\) | \(1.124\) | \(94.3\) |
| \(\tau_{\textsubscript{NIE}}(1)\) | \(1.93\) | \(4.65\) | \(1.250\) | \(1.231\) | \(94.4\) |
| \(\tau_{\textsubscript{NDE}}(0)\) | \(3.27\) | \(1.21\) | \(1.249\) | \(1.230\) | \(94.9\) |
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.88\) | \(3.56\) | \(0.744\) | \(0.731\) | \(96.2\) |
| \(\tau_{\textsubscript{NDE}}(1)\) | \(4.32\) | \(0.28\) | \(1.334\) | \(1.305\) | \(95.4\) |
| \(n = 1000\), \(T = 20\) | |||||
| \(\tau_{\textsubscript{TE}}\) | \(5.20\) | \(1.20\) | \(0.330\) | \(0.347\) | \(92.6\) |
| \(\tau_{\textsubscript{NIE}}(1)\) | \(1.95\) | \(8.73\) | \(0.336\) | \(0.336\) | \(92.0\) |
| \(\tau_{\textsubscript{NDE}}(0)\) | \(3.25\) | \(3.35\) | \(0.354\) | \(0.363\) | \(93.1\) |
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.89\) | \(8.27\) | \(0.211\) | \(0.211\) | \(94.2\) |
| \(\tau_{\textsubscript{NDE}}(1)\) | \(4.31\) | \(0.31\) | \(0.397\) | \(0.410\) | \(93.8\) |
| \(n = 100\), \(T = 20\) | |||||
| \(\tau_{\textsubscript{TE}}\) | \(5.20\) | \(1.02\) | \(1.139\) | \(1.174\) | \(93.5\) |
| \(\tau_{\textsubscript{NIE}}(1)\) | \(1.95\) | \(7.67\) | \(1.293\) | \(1.333\) | \(93.2\) |
| \(\tau_{\textsubscript{NDE}}(0)\) | \(3.25\) | \(3.41\) | \(1.275\) | \(1.295\) | \(94.5\) |
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.89\) | \(8.98\) | \(0.802\) | \(0.827\) | \(94.6\) |
| \(\tau_{\textsubscript{NDE}}(1)\) | \(4.31\) | \(1.19\) | \(1.394\) | \(1.400\) | \(95.1\) |
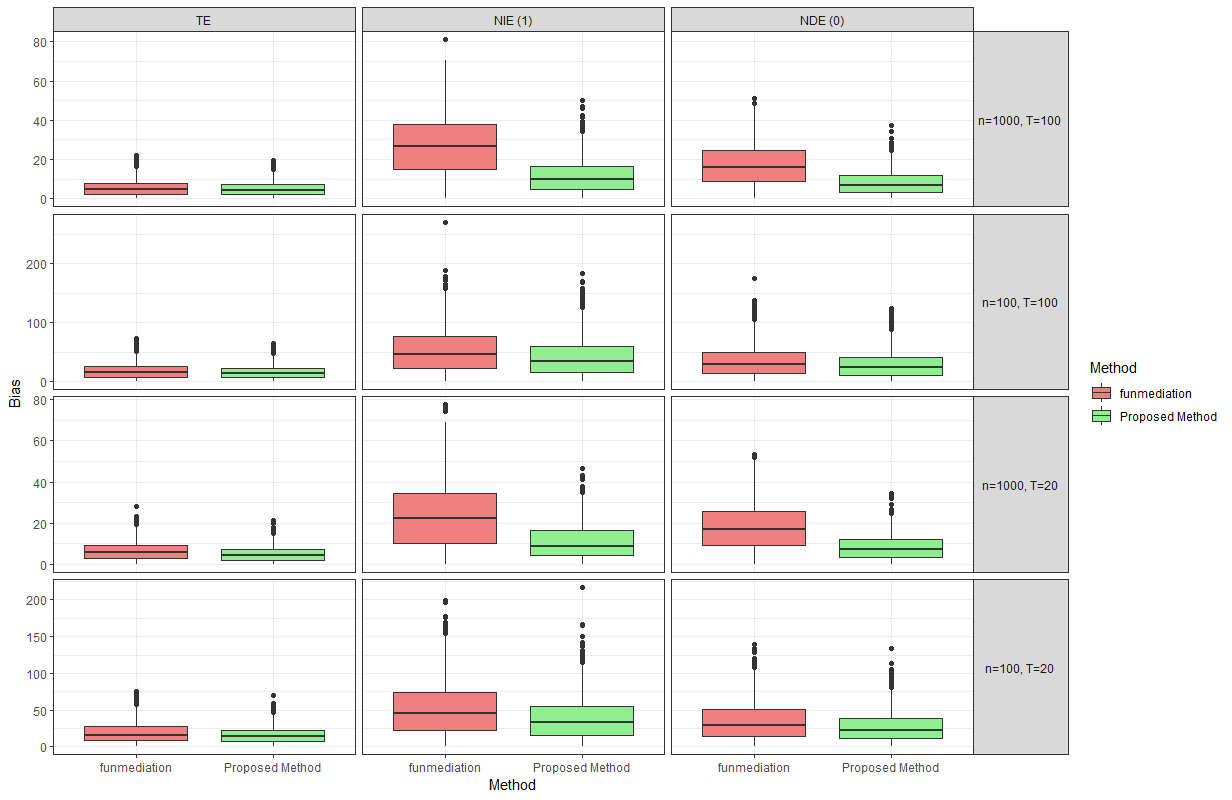
Figure 4: A comparison of percent absolute bias in \(R = 1000\) simulation replications between the proposed method and funmediation under a simple functional mediator.
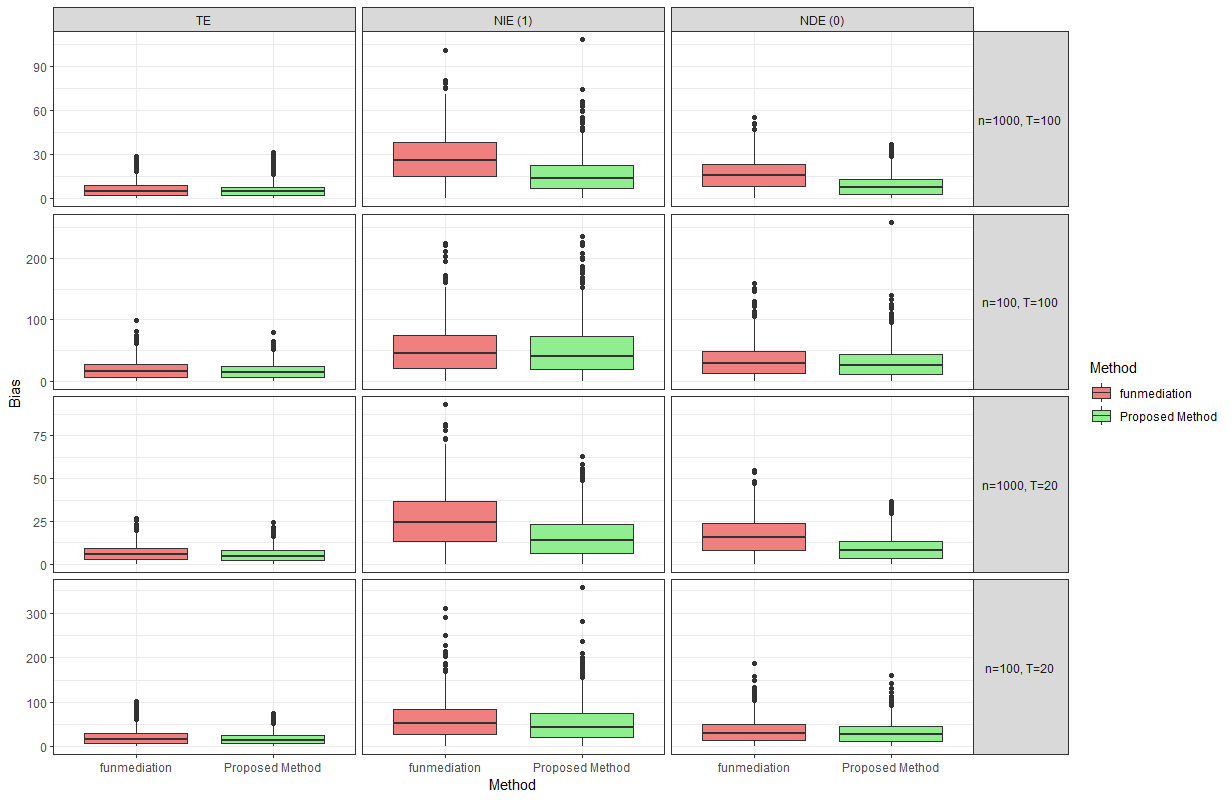
Figure 5: A comparison of percent absolute bias in \(R = 1000\) simulation replications between the proposed method and funmediation under a complex functional mediator
After implementing the proposed methods, we obtain a point estimate, a sample standard deviation and a \(95\%\) confidence interval for each of the causal direct, indirect and total effects for each of the \(R = 1000\) replication datasets. We use the total effect as an example to illustrate the calculation of the percent absolute bias (BIAS), empirical coverage probability (ECP), average standard errors (ASE), and empirical standard errors (ESE). For the \(r\)-th replication dataset, where \(r = 1, \ldots, R\), we denote the point estimate as \(\widehat{\tau}^r_{\textsubscript{TE}}\), the sample standard deviation as \(\widehat{\sigma}^r_{\textsubscript{TE}}\), and the \(95\%\) confidence interval as \(\text{CI}_{95\%}^r(\tau_{\textsubscript{TE}})\). The performance measures are calculated as follows, \[\begin{align} \text{BIAS} &= \frac{|\sum_{r=1}^R\widehat{\tau}^r_{\textsubscript{TE}} / R - \tau_{\textsubscript{TE}}|}{|\tau_{\textsubscript{TE}}|} \times 100\%,\\ \text{ECP} &= \frac{\sum_{r = 1}^R\mathbb{1}(\tau_{\textsubscript{TE}} \in \text{CI}_{95\%}^r(\tau_{\textsubscript{TE}}))}{R} \times 100\%,\\ \text{ASE} &= \frac{\sum_{r = 1}^{R}\widehat{\sigma}^r_{\textsubscript{TE}}}{R},\\ \text{ESE} &= \sqrt{\frac{\sum_{r=1}^{R}\left(\widehat{\tau}^r_{\textsubscript{TE}}-\sum_{r=1}^R\widehat{\tau}^r_{\textsubscript{TE}}/ R\right)^2}{R-1}}, \end{align}\] where \(\tau_{\textsubscript{TE}}\) refers to the true total effect.
Tables 1 and 2 summarise the empirical results from the simulation studies. It can be observed that the proposed method performs reasonably well across the eight scenarios. The method generally yields little bias when estimating the causal effects. Variability in effect estimates is consistent among different scenarios. The empirical coverage probabilities are close to the nominal \(95\%\). The complexity of the functional form of the mediator presents itself as the most important factor affecting the performance of the proposed method in estimating the causal effects. We observe a general pattern of increased bias, variability and lower coverage probabilities in scenarios with a complex functional mediator compared to a simple one. Despite not having notable impacts on the bias and variability of the effect estimates, a smaller sample size consistently results in larger variability, as expected. The number of observations of the functional mediator over the time period does not appear to considerably affect any performance measure under a simple functional mediator, while a decrease in it does cause increased bias under a complex functional mediator. This may be attributed to the fact that there is little loss of information due to fewer observations for a simple function.
Overall, the proposed method shows solid performance across the scenarios, particularly when applied to a large sample of subjects with a frequently observed simple functional mediator. The complexity of the functional form of the mediator is the most influential factor, as a more complex mediator adversely impacts all performance measures and significantly increases computation time. Coverage probabilities are reasonably close to the ideal \(95\%\) in most scenarios, indicating that the method is reasonably robust.
We compare the proposed methods to an existing R package funmediation, which also performs functional causal mediation analysis for an end-point outcome [19]. Specifically, methods in funmediation assume confounding variables and a binary treatment at baseline, a functional mediator, and an end-point continuous or binary outcome, by adopting linear functional
structural equation models similar to those in [18]. Obviously, funmediation is not intended for our settings where the outcome is a
zero-inflated count. First, the outcome scalar-on-function regression models used by funmediation assume either a Gaussian distribution or Bernoulli distribution for the outcome, which is inadequate for count data, especially one with excess
zeros. Second, the linear functional structural equation models imply the equivalence between \(\tau_{\textsubscript{NIE}}(1)\) and \(\tau_{\textsubscript{NIE}}(0)\), and thus also between
\(\tau_{\textsubscript{NDE}}(0)\) and \(\tau_{\textsubscript{NDE}}(1)\). However, this is not the case when nonlinearity is present between the treatment, mediator, and outcome, which means
the use of linear models cannot capture this in our settings. Figures 4 and 5 compare the percent absolute bias of the effect estimates in \(R=1000\) replications of simulation studies using the proposed method and funmediation, where we “naively" ignore that fact that the outcome is a zero-inflated count and apply funmediation as if it was
continuous. The estimands being compared are \(\tau_{\textsubscript{TE}}\), \(\tau_{\textsubscript{NIE}}(1)\) and \(\tau_{\textsubscript{NDE}}(0)\). It can
be observed that while funmediation performs reasonably close to the proposed methods when estimating the total effect, it fails to reliably estimate the natural direct and indirect effects across all data-generating mechanisms. Therefore, the
proposed methods offer a more suitable approach for reliably estimating causal effects in the context of a functional mediator and a zero-inflated count outcome. By addressing the limitations of linear models and capturing the nonlinearity between
treatment, mediator, and outcome, the methods provide an effective framework for distinguishing between natural direct and indirect effects across different treatment statuses in causal mediation analysis.
5 Gender, central venous pressure, and rehospitalisations after CABG in MIMIC-IV↩︎
Our research question in this paper is two-fold. Firstly, we would like to investigate the causal effect of gender on the number of hospital readmissions within 60 days of discharge from the primary hospital stay among patients who underwent CABG in the MIMIC-IV database. Secondly, we intend to examine whether the time-varying CVP measured over the post-surgical ICU stay mediates the causal pathway from gender to rehospitalisations. Consequently, we arrive at a functional causal mediation analysis with a zero-inflated count outcome, with gender being a binary treatment, time-varying CVP during the postoperative ICU stay being a functional mediator, and the 60-day readmission count as a zero-inflated count outcome. The procedures for extracting data from MIMIC-IV, as well as the research question in the context of the final study data are introduced in Section 5.1. Section 5.2 provides a discussion of the findings and insights.
5.1 Study data from MIMIC-IV↩︎
For this study, all data were retrieved from version 2.2 of the Medical Information Mart for Intensive Care IV (MIMIC-IV) database. MIMIC-IV is a large publicly available electronic health record (EHR) database containing 299,712 patients, 431,231 hospital admissions, and 73,181 ICU stays. The database, sourced from an EHR system of the hospital and a clinical information system of the ICU, includes all deidentified medical records corresponding to patients admitted to an ICU or the emergency department of the Beth Israel Deaconess Medical Center (BIDMC) between 2008 and 2019.

Figure 6: A flow chart of cohort selection procedures from MIMIC-IV.
A total of 5,655 patients in MIMIC-IV who underwent CABG were identified using the Ninth and Tenth Revisions of the International Classification of Diseases (ICD-9 code 361 and ICD-10 code 021). The final cohort was formed using the following exclusion criteria: (a) patients who were not transferred to ICU at the primary CABG hospital admission or transferred more than 1 day after surgery; (b) patients who died at the primary CABG hospital admission; (c) patients who did not have CVP measurements during the post-surgical ICU stay. As demonstrated in Figure 6, 4,962 patients were finally selected for our analysis.
As Table 3 displays, demographics, hospital admission and ICU stay records, comorbidities, vital signs, laboratory test results, and ICU electronic charts were collected. Note that the baseline time is defined as either the time of primary CABG hospital admission for patient demographics and comorbidities or post-surgical ICU admission for scores. Demographic data include gender, age at admission, race, height, weight, and date of death. Records of hospital admission and ICU stay include times of admission and discharge. Comorbidities used to calculate the Charlson Comorbidity Index (CCI) score were obtained, including myocardial infarction (MI), congestive heart failure (CHF), peripheral vascular disease (PVD), cerebrovascular disease, chronic obstructive pulmonary disease (COPD), diabetes, liver diseases, renal failure and others [46]. Information from vital signs, laboratory results and electronic charts includes heart rate, various blood pressure measurements, body temperature, albumin, white blood cells (WBC), neutrophils, blood urea nitrogen (BUN), and so on. These measurements are summarised into scores, including the Logistic Organ Dysfunction System (LODS) score, the Oxford Acute Severity of Illness Score (OASIS), Simplified Acute Physiology Score II (SAPS II), Systemic Inflammatory Response Syndrome (SIRS) criteria, and Glasgow Coma Scale (GCS) [47].
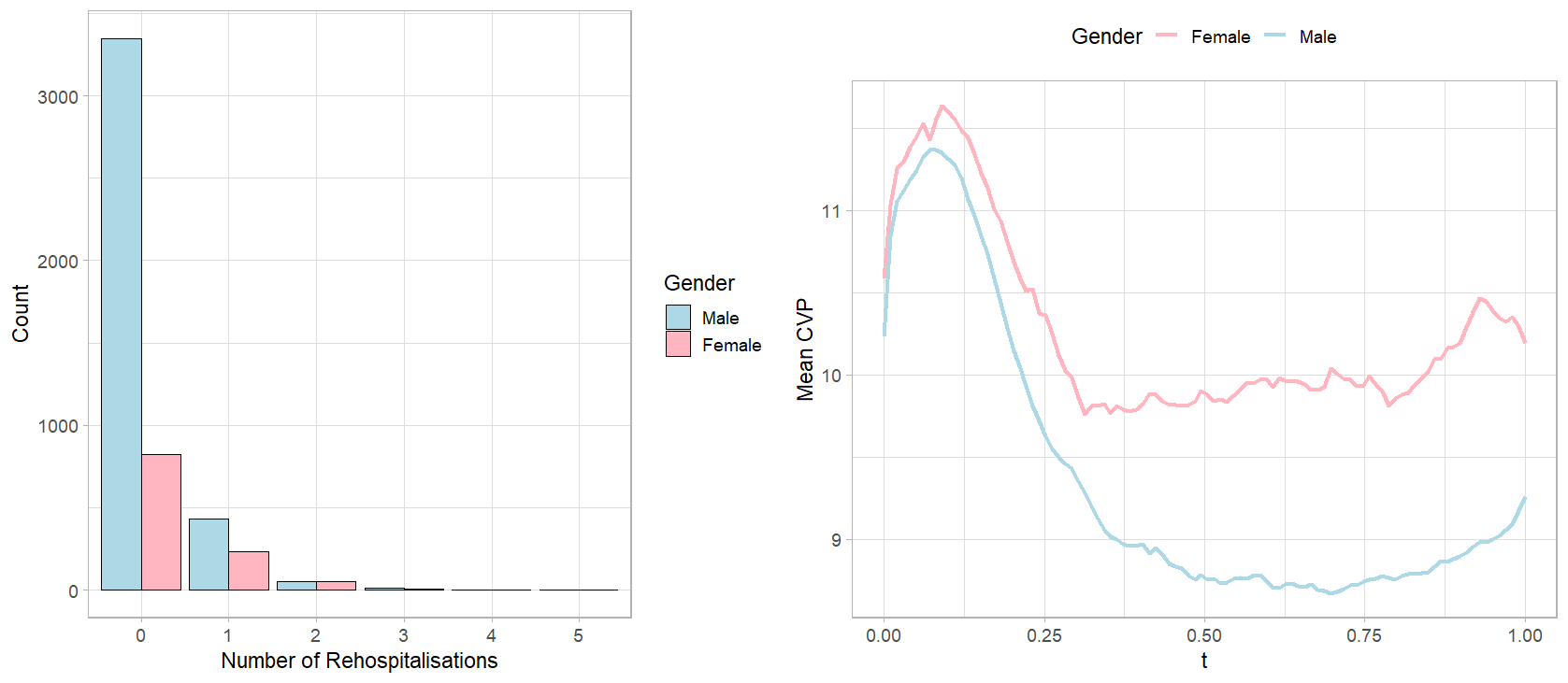
Figure 7: Left panel: a comparison of distributions of 60-day rehospitalisations after CABG between genders. Right panel: a comparison of observed CVP measurements during post-surgical ICU stay averaged within genders.
| Univariate p-value | ||||
|---|---|---|---|---|
| 3-5 Variable | Summary | Treatment | Mediator | Outcome |
| (\(n=4962\)) | (Gender) | (CVP) | (60-day readmissions) | |
| Age (years) | \(68.20 \pm 10.20\) | \(< 0.001\) | \(0.313\) | \(0.689\) (\(< 0.001\)) |
| Ethnicity, \(n(\%)\) | \(< 0.001\) | \(0.029\) | \(0.028\) (\(0.551\)) | |
| Black | \(183\) (\(3.7\)) | |||
| Others | \(4779\) (\(96.3\)) | |||
| Baseline CVP (mmHg) | \(10.31 \pm 4.68\) | \(0.028\) | \(< 0.001\) | \(0.087\) (\(0.690\)) |
| Comorbidities, \(n(\%)\) | ||||
| Myocardial infarction | \(1881\) (\(37.9\)) | \(0.056\) | \(0.007\) | \(0.996\) (\(0.356\)) |
| Congestive heart failure | \(1176\) (\(23.7\)) | \(< 0.001\) | \(< 0.001\) | \(0.030\) (\(0.429\)) |
| Peripheral vascular disease | \(638\) (\(12.9\)) | \(0.001\) | \(< 0.001\) | \(0.762\) (\(0.218\)) |
| Cerebrovascular disease | \(503\) (\(10.1\)) | \(< 0.001\) | \(0.041\) | \(0.400\) (\(0.552\)) |
| Dementia | \(25\) (\(0.50\)) | \(0.767\) | \(0.013\) | \(0.895\) (\(0.898\)) |
| Chronic pulmonary disease | \(940\) (\(18.9\)) | \(< 0.001\) | \(< 0.001\) | \(0.295\) (\(0.174\)) |
| Rheumatic disease | \(145\) (\(2.9\)) | \(< 0.001\) | \(0.364\) | \(0.259\) (\(0.635\)) |
| Peptic ulcer disease | \(37\) (\(0.75\)) | \(0.786\) | \(0.112\) | \(0.337\) (\(0.210\)) |
| Liver disease | \(7\) (\(0.14\)) | \(0.608\) | \(0.084\) | \(0.698\) (\(0.940\)) |
| Diabetes | \(156\) (\(3.1\)) | \(0.054\) | \(0.459\) | \(0.114\) (\(0.480\)) |
| Paraplegia | \(38\) (\(0.77\)) | \(0.014\) | \(0.066\) | \(0.799\) (\(0.860\)) |
| Renal disease | \(878\) (\(17.7\)) | \(0.908\) | \(< 0.001\) | \(0.003\) (\(0.670\)) |
| Malignant cancer | \(137\) (\(2.8\)) | \(0.070\) | \(0.794\) | \(< 0.001\) (\(0.855\)) |
| Metastatic solid tumor | \(12\) (\(0.24\)) | \(0.632\) | \(0.159\) | \(0.260\) (\(0.894\)) |
| AIDS/HIV | \(5\) (\(0.10\)) | \(0.959\) | \(0.670\) | \(0.531\) (\(0.946\)) |
| Scores | ||||
| CCI | \(4.38 \pm 2.23\) | \(< 0.001\) | \(< 0.001\) | \(0.012\) (\(< 0.001\)) |
| LODS | \(4.78 \pm 2.44\) | \(0.102\) | \(< 0.001\) | \(0.157\) (\(0.613\)) |
| OASIS | \(33.27 \pm 6.84\) | \(< 0.001\) | \(< 0.001\) | \(0.285\) (\(0.168\)) |
| SAPSII | \(39.01 \pm 11.40\) | \(< 0.001\) | \(< 0.001\) | \(0.517\) (\(0.628\)) |
| SIRS | \(2.77 \pm 0.82\) | \(0.079\) | \(< 0.001\) | \(0.202\) (\(0.187\)) |
| GCS | \(13.18 \pm 3.75\) | \(0.740\) | \(0.003\) | \(0.845\) (\(0.211\)) |
Note: P-values for each baseline covariate from the univariate ZIP outcome model are presented, with the p-value for the count component shown outside the parentheses and the p-value for the zero-inflation component shown inside. CCI = Charlson Comorbidity Index; LODS = Logistic Organ Dysfunction System; OASIS = Oxford Acute Severity of Illness Score; SAPSII = Simplified Acute Physiology Score II; SIRS = Systemic Inflammatory Response Syndrome; GCS = Glasgow Coma Scale.
The difference in the number of 60-day hospital readmissions after CABG surgery is straightforward in the left panel of Figure 7, with considerably more male patients having no readmission at all than female patients. This motivates a causal analysis of whether there is a causal effect of gender on 60-day rehospitalisation counts. We use curves in the right panel of Figure 7 to reveal the difference in the discrete CVP measurements over postoperative ICU stay averaged over male and female patients. While women have consistently higher CVP measurements than men on average, the shapes of the trajectories are intriguing. The mean CVP curves for males and females both show an initial peak followed by a gradual decline, eventually stabilizing over time. Although both curves follow a similar pattern, the mean CVP curve for female patients settles at a notably higher level than that of male patients. Along with evidence of CVP’s prognostic role for post-CABG complications, we aim to examine the mediating effect of not only the baseline CVP measurement but the entire CVP process. Other baseline covariates, such as age, race, comorbidities, and scores are candidates for confounding variables. According to Table 3, we select the confounding variables as the baseline covariates that are significantly associated, at \(20\%\) significance level, with at least two of: (a) the treatment; (b) the mediator; (c) the outcome count component; (d) the outcome zero component. We also include pre-existing liver disease which does not meet the significance criteria but is empirically found by the literature to be related to hospital readmissions after CABG. [10], [12]. Additionally, our analysis also adjusts for the baseline CVP level, that is, the first CVP measurement taken in the post-surgical ICU stay, per advice from [48]. The treatment-mediator interaction is excluded due to lack of significance.
5.2 Findings and insights↩︎
We posit the causal framework described in Section 2 and apply the proposed methods from Section 3 to investigate the causal relationship between gender, time-varying CVP and 60-day hospital readmissions after CABG. Section 5.2.1 presents findings from functional data analysis related to time-varying CVP. We discuss the results and insights provided by causal mediation analysis in 5.2.2.
5.2.1 Results from functional data analysis↩︎
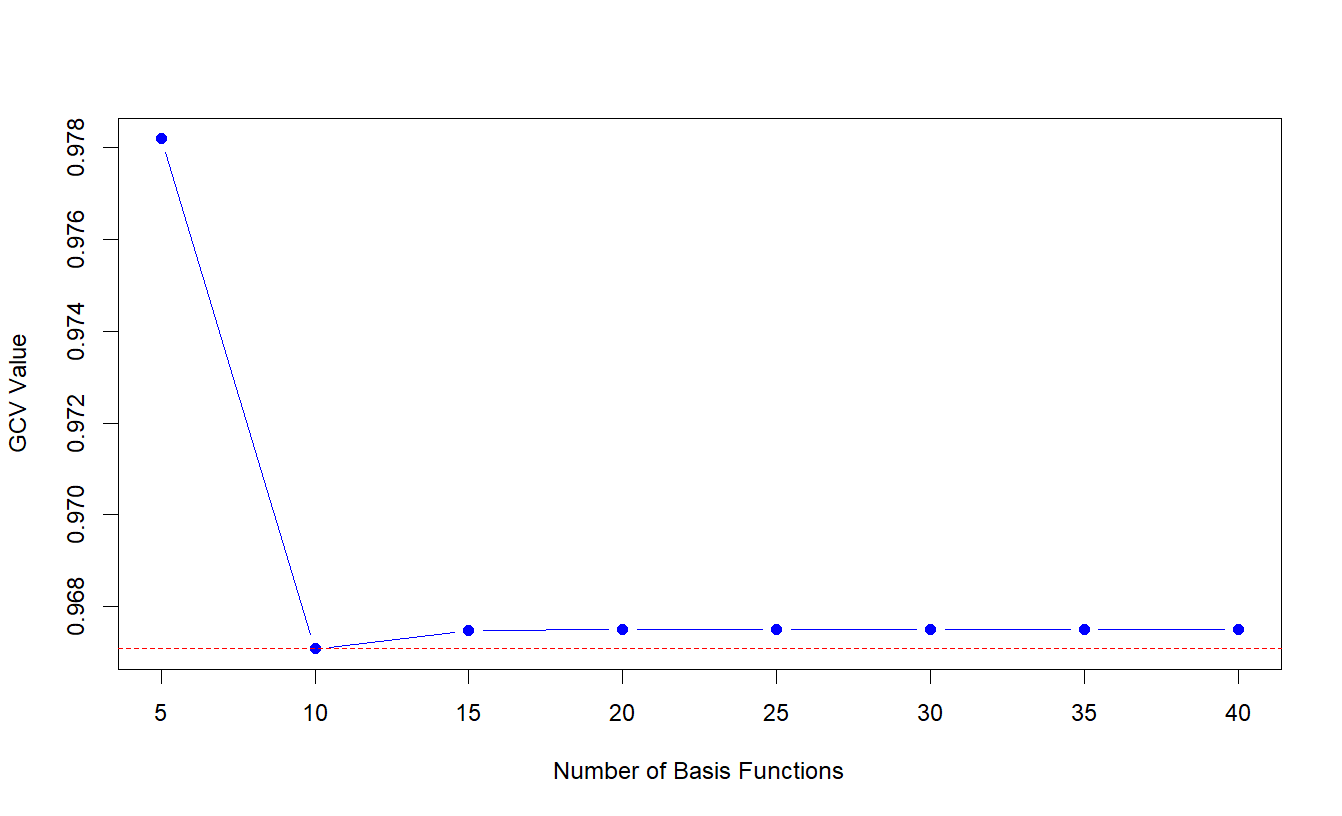
Figure 8: Values of the GCV criterion with corresponding number of cubic spline basis functions.
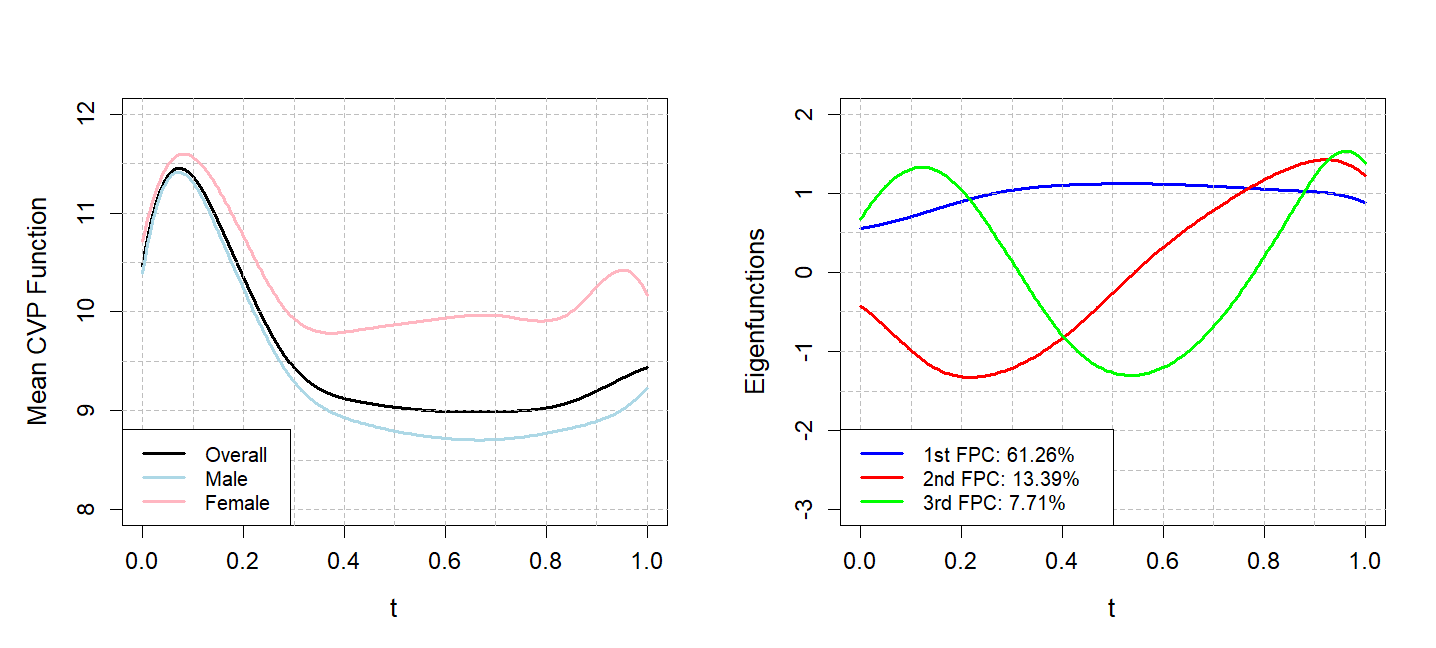
Figure 9: Left panel: the overall, male and female mean functions of the mediator, that is, the CVP function in the post-surgical ICU stay. Right panel: the first three FPCs of the CVP function.
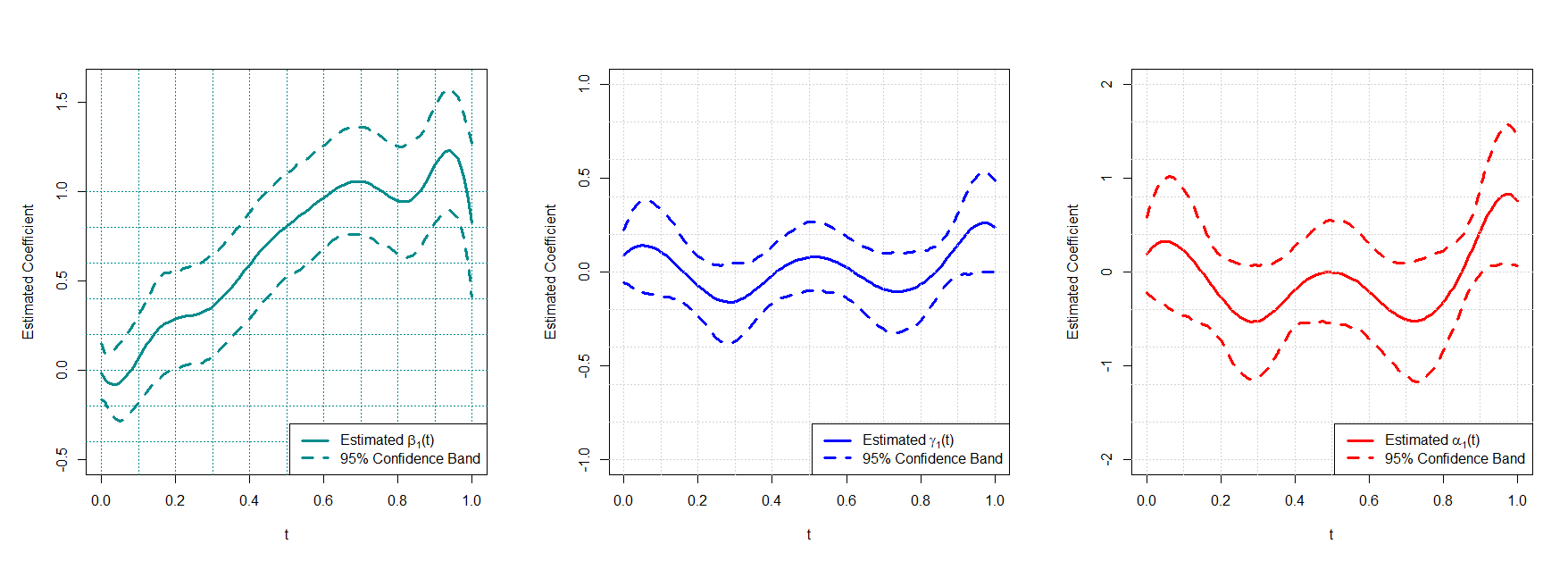
Figure 10: Estimated coefficient functions from the mediator and outcome models: the estimated coefficient function for the treatment gender in the mediator model \(\widehat{\beta}_1(t)\) (left panel); the estimated coefficient function for the mediator CVP function in the outcome model count component \(\widehat{\gamma}_1(t)\) (middle panel); the estimated coefficient function for the mediator CVP function in the outcome model zero component \(\widehat{\alpha}_1(t)\).
The generalised cross-validation (GCV) criterion is a measure of the lack of fit, adjusted for the degrees of freedom. Typically, the lower the GCV value, the better the model strikes a balance between fitting the data well and maintaining simplicity [41]. Per Figure 8, the GCV criterion is used to select the number of cubic spline basis functions to impute the smooth CVP process underlying the discrete CVP measurements over the post-surgical ICU stay. As indicated by the minimum GCV, ten cubic spline basis functions were used, yielding the mean CVP functions in the left panel of Figure 9. Consistent with the right panel of Figure 7, the mean underlying CVP function for female patients is higher than that of males over the entire time range. Five FPCs of the CVP function, which explain over \(90\%\) of total variance, are used to estimate the functional ZIP outcome model. The right panel of Figure 9 displays the first three FPCs of the CVP function, explaining approximately \(61\%\), \(13\%\) and \(8\%\) of the total variation, respectively. The first component is relatively stable over time, with only a gradual increase followed by a slight decrease, representing an overall shift in the mean CVP level across the period. The second component has a distinct sinusoidal pattern, first decreasing and then increasing sharply. The third component oscillates more rapidly, capturing finer-scale fluctuations and higher-frequency variability in CVP over time.
The estimated coefficient functions from the mediator and outcome models are shown in Figure 10. \(\widehat{\beta}_1(t)\) in the left panel represents the estimated functional coefficient for gender in the function-on-scalar regression, Model (4 ), for the CVP function, which can be interpreted as the partial effect of gender on the CVP function at time \(t\). An overall upward trend is evident throughout the time span, corroborating with the widening gap between the mean CVP function of genders as seen in Figure 9. Recall that the functional ZIP model for 60-day rehospitalisations is of the form in (8 ), (9 ) and (10 ), where \(\gamma_1(t)\) and \(\alpha_1(t)\) are the coefficient functions for the CVP function. They represent the weight of the CVP level at time \(t\) in determining the rate of the Poisson component and the probability of being an excess zero in the binary component, respectively. The middle and right panels demonstrate their estimates and a similar pattern of fluctuations can be observed.
5.2.2 Results from causal mediation analysis↩︎
| Point Estimate | SE | \(95\%\) CI | |||
|---|---|---|---|---|---|
| \(\tau_{\textsubscript{TE}}\) | \(0.140\) | \(0.020\) | \((0.101, 0.178)\) | ||
| \(\tau_{\textsubscript{NIE}}(1)\) | \(0.008\) | \(0.003\) | \((0.002, 0.014)\) | ||
| \(\tau_{\textsubscript{NDE}}(0)\) | \(0.132\) | \(0.020\) | \((0.093, 0.170)\) | ||
| \(\tau_{\textsubscript{NIE}}(0)\) | \(0.005\) | \(0.002\) | \((0.001, 0.009)\) | ||
| \(\tau_{\textsubscript{NDE}}(1)\) | \(0.135\) | \(0.020\) | \((0.096, 0.173)\) | ||
Table 4 summarises the point estimate, standard error and \(95\%\) confidence interval for the estimated total effect, the natural direct and indirect effects from the functional causal mediation analysis with a zero-inflated count outcome. After adjusting for confounding variables and baseline CVP measurement, we observe a statistically significant total effect of gender on the number of hospital readmissions within 60 days of discharge from primary CABG admission. Firstly, according to evidence found by the proposed methods, female patients, compared to male patients, in MIMIC-IV suffer an average increase of 0.14 hospital readmissions within 60 days after undergoing CABG surgery.
Secondly, the total effect is found to be significantly mediated by the smooth function underlying CVP levels measured during the post-surgical ICU stay. For example, we estimate \(\tau_{\textsubscript{NIE}}(1)\) to be approximately \(0.008\). This means that being a female patient but having the CVP level of that of a man during the ICU stay after taking a CABG surgery can reduce the number of 60-day hospital readmissions by \(0.008\). Furthermore, \(0.008\) amounts to approximately \(5.7\%\) of the total effect, indicating that \(5.7\%\) of the effect of gender on 60-day rehospitalisation counts can be explained by the time-varying CVP level during the post-surgical ICU stay of the patient.
The above findings on the causal relationships between gender, CVP, and rehospitalisations after CABG align with existing studies on cardiac surgery, offering insights into the gender disparities in postoperative complications. It is established that women who undergo CABG surgery experience more hospital readmission, even when accounting for age, race, comorbidities, and other baseline health indicators. We further demonstrate that this adverse effect can be partly explained by differences in CVP levels between genders during the post-surgical ICU stay. These results shed light on the underlying biological factors contributing to sex disparities in postoperative outcomes, with the significant mediating effect of CVP possibly linked to differences like the thinner vessels observed in females.
6 Discussion↩︎
To investigate the causal pathway from gender to 60-day rehospitalisation counts among patients who underwent CABG surgery in the MIMIC-IV database, we propose a framework for causal mediation analysis with a functional mediator and a zero-inflated count outcome, as well as methods to estimate the causal effects. Specifically, with a functional mediator, we formalise the potential outcomes framework and discuss the definition of causal effects and the identifying assumptions for the effects. A function-on-scalar regression is used to model the functional mediator, and a functional zero-inflated Poisson model is used to address the previously understudied relationship between a zero-inflated count outcome and a functional mediator. Nonparametric identification results [33], [39] are adapted to our setting with a functional mediator to facilitate the parameter-based Monte Carlo approximation algorithm for the estimation and inference of causal effects. Simulation studies validate the performance of the proposed methods in estimating the causal effects in different sample sizes, numbers of observations over the time span, and levels of complexity of the functional mediator.
With the selected cohort of CABG patients from MIMIC-IV, we establish both a significant total effect of gender on the number of readmissions and a significant mediating effect on this pathway by the time-varying CVP level during post-surgical ICU stay. Since the early evidence from the likes of [49] and [50], it has long been acknowledged in the literature that the outcomes for women following CABG differ from those of men. In this context, our findings not only confirm the inferior outcomes in terms of rehospitalisations for female patients but also aid in the effort to uncover the underlying causes of such disparities and provide directions for bridging this gap. In particular, while plenty of statistical analyses concerning the matter focus on reasons related to health equity such as referral bias [8], we discover that postoperative changes in CVP level potentially as a consequence of innate biological differences between genders also play a significant role. Consequently, evidence from our analysis suggests that clinical practitioners could monitor and manage elevated CVP levels post-surgery to reduce hospital readmissions
It should be noted that the proposed parameter-based Monte Carlo approximation algorithm can accommodate different models for the mediator and outcome. Therefore, an immediate future direction of methodological development is to incorporate different models for the zero-inflated count outcome, such as the functional hurdle model and the functional negative binomial model. Furthermore, the algorithm may even be employed to study other types of outcomes, for example, binary outcomes, that invoke nonlinearity and call for the use of other generalised functional linear models. Another area for future research arises from an important limitation of the proposed method, which is its computational complexity. Several articles [25], [26], [51], [52] have demonstrated the use of similar simulation-based approaches for causal mediation analysis with a zero-inflated count outcome in a non-functional setting, where computational intensity is already a problem. As the result of involving functional linear and nonlinear models, the use of the proposed method can be even more computationally intensive, especially for large datasets. Naturally, deriving a theoretically sound analytical solution to the causal effects with a functional mediator and a zero-inflated count outcome is an important future direction of work. Currently, our work focuses on data observed on even and dense grids. However, in many disciplines, longitudinal measurements are often collected infrequently and irregularly. For example, in behavioural studies, participants may miss prompts that they should have responded to, leading to gaps in the data. Addressing sparse functional data in nonlinear settings is therefore a crucial next step for advancing this research.