Impact of Dark Matter and Rotation on Neutron Star Properties
September 02, 2024
Abstract
In this study, we examine the combined effects of dark matter (DM) and rotation on the properties of neutron stars (NSs). We employ a self-interacting dark matter model, motivated by the neutron decay anomaly, within the relativistic mean-field formalism to explore its impact on both static and rotating NSs. The Hartle-Thorne approach is utilized to model rotating NSs, treating the DM interaction strength (\(G\)) as a free parameter and considering angular velocity (\(\Omega\)) for rotation. We investigate how DM influences the mass-shedding limit, determined using the Keplerian frequency, and analyze the variations in angular velocity at different DM interaction strengths to assess their effects on NS mass, radius, central energy density, and eccentricity. Our results indicate that while rotation increases mass and radius due to centrifugal forces, DM softens the EOS, reducing these properties, particularly at higher DM fractions. DM also reduces rotational deformation, leading to lower eccentricity compared to DM-free NSs at the same angular velocity. Additionally, we calculate the relative deviations in maximum rotational mass and canonical equatorial radius from their baseline values, finding that high DM fractions combined with low angular velocities result in significant reductions, while low DM fractions with high rotational speeds lead to positive deviations, indicating greater deformation.
1 Introduction↩︎
Dark matter (DM) and rotation are critical factors in studying neutron stars (NS) due to their significant influence on the star’s structural and dynamical properties. Neutron stars provide a unique laboratory for exploring physics under extreme conditions, where high densities and strong gravitational fields push matter beyond nuclear saturation density (\(n_0 = 0.15 \, \text{fm}^{-3}\)) [1]–[3]. Validating the equations of state (EOS) for matter at these densities is crucial, as the behavior of such dense matter remains poorly understood. The macroscopic properties of NSs—such as mass, radius, compactness, and rotational deformation—are directly dependent on the EOS and can be theoretically modeled to compare with observational data, offering insights into the nature of dense matter [4]–[9]. While non-rotating, spherically symmetric NSs can be accurately modeled using the Tolman-Oppenheimer-Volkoff (TOV) equations [10], [11], the inclusion of rotation introduces significant deformations that require more sophisticated approaches.
Firstly, the rotation for the NS was introduced with Hartle-Throne formalim [12], [13]. Recent studies have advanced our understanding of rotating neutron stars (RNS) through various approaches [14]–[24]. For instance, the impact of \(f(R,T)\) gravity on rapidly rotating NSs has been investigated through a modified gravity framework [21]. Other works, such as Patterson et al. [20], examine mass correction and deformation in slowly rotating anisotropic stars using the Hartle-Thorne formalism, while Lopes [23] analyzes the effects of different symmetry energy slopes (\(L\)) on both static and slowly rotating NSs and attempt to constrain \(L\) values based on observations of recently discovered 33 millisecond pulsars [25]. Additionally, several studies have explored the influence of DM on various properties of RNS. Guha et al. investigated DM-SM interactions in RNS with different mediators [19], while in Ref. [22], the author studied rotating DM admixed NSs using a two-fluid approach. Andreas also utilized a two-fluid model to examine how a DM core affects the structure of RNS [24]. These studies highlight the complexity and significance of both DM and rotation in determining NS properties.
DM is believed to constitute a substantial portion of the Universe’s mass-energy content, with its existence supported by various astrophysical and cosmological observations, including cosmic microwave background radiation, large-scale structure formation, and galaxy rotation curves [26]. Several candidates for DM have been proposed, such as weakly interacting massive particles (WIMPs) and QCD axions [26], [27]. In the context of neutron stars, different models have been developed to study the effects of DM. Some studies employ a two-fluid framework, exploring gravitational interactions that suggest the possible presence of DM within the NS or extending to a halo structure [28]–[32]. Other research focuses on non-gravitational interactions, treating the NS and DM as a single fluid and considering the presence of DM within the NS [33]–[42]. Despite ongoing research, the precise nature and properties of DM remain elusive, continuing to fuel scientific inquiry.
In this study, we employ a single-fluid model inspired by the neutron decay anomaly, assuming DM accumulates within the NS core [43]–[48]. We investigate the combined effects of DM and rotation on the different properties of the NS. First, we develop a DM-admixed NS equation of state within the relativistic mean-field (RMF) framework, which is ideal for describing matter under extreme densities by incorporating mesonic interactions that mediate nuclear forces [49], [50]. For the RNS case, we utilize the Hartle-Thorne formalism for slow rotation [12], [13] , up to a conservative maximum of \(\Omega = 5000 \, \text{s}^{-1}\). This limit is chosen to maintain the validity of the slow rotation approximation, considering the fastest known pulsar, PSR J1748-2446ad, which spins at 4498 \(\text{s}^{-1}\) [51]. Also, we explore the implications of rotation at the mass-shedding limit defined by the Keplerian frequency, which is essential for understanding the stability of rapidly rotating neutron stars [14], [23]. After establishing the DM admixed NS and RNS formalism, we fix the interaction strength as a free parameter to vary the amount of DM within the NS and adjust the angular velocity to observe the effects of rotation on NS properties. We then study how different properties of the NS are influenced by varying rotation while keeping the DM interaction strength constant. Since both DM and rotation significantly affect NS properties, we ultimately calculate the relative deviation of the rotational mass and equatorial radius from their baseline values (i.e., the values for a static NS with no DM).
This paper is structured as follows: Section 2.1 introduces the DM model based on the neutron decay anomaly. Section 2.2 details the development of the EOS for DMANS, incorporating the NITR parameter set and contributions from leptons. Section 2.3 discusses the single-fluid TOV equations for determining the equilibrium structure of static DM admixed NS. Section 2.3.2 outlines the Hartle-Thorne formalism for slowly rotating NS. The results are presented in Section 3, followed by a summary and conclusions in Section 4.
2 Formalism↩︎
2.1 Dark Matter Model↩︎
In this study, we employ a DM model inspired by the neutron decay anomaly, which may account for the discrepancy in the neutron lifetime measured by two distinct experimental techniques: beam experiments [52] and bottle experiments [53]. According to Fornal and Grinstein [43], if 1% of neutrons decay into the dark sector, this anomaly could be resolved. They proposed a decay channel where a neutron decays into a light dark boson (\(\phi\)) and a fermion (\(\chi\)) with baryon number 1:
\[n \longrightarrow \chi + \phi.\]
Nuclear stability imposes constraints on the masses of these dark particles, requiring that \(937.993 \, \text{MeV} < m_\chi + m_\phi < 939.565 \, \text{MeV}\) [45]. Furthermore, for \(\chi\) and \(\phi\) to be viable DM candidates, their stability necessitates the mass bound \(|m_\chi - m_\phi| < m_p + m_e = 939.783 \, \text{MeV}\) [45]. In this work, we assume the scalar boson to be massless (\(m_\phi = 0\)) and set the mass of the dark fermion to \(m_\chi = 938.0 \, \text{MeV}\). The boson \(\phi\) is assumed to escape the system with minimal interaction, establishing an equilibrium condition between the neutron and the dark fermion [46]–[48]: \[\mu_\chi = \mu_n.\]
2.2 Equation Of State for DM admixed NS↩︎
For the current study, we employ a relativistic mean-field (RMF) model named “NITR" [54] to determine the EOS for NSs with DM admixture. To obtain the EOS for DM-admixed NSs, we incorporate self-interacting dark matter (SIDM) within the RMF formalism. In this formalism, nucleons interact via the exchange of mesons, and we consider three types of mesons: the scalar \(\sigma\), the vector \(\omega\), and the isovector \(\rho\) mesons. The Lagrangian describing nucleonic matter is given by [54]–[58]: \[\begin{align} \mathcal{L}_{\text{nuc}} &= \sum_{\alpha=n,p} \bar{\psi}_{\alpha} \left[ \gamma_{\mu} \left( i\partial^{\mu} - g_{\omega} \omega^{\mu} - \frac{1}{2} g_{\rho} {\tau} \cdot {\rho}^{\mu} \right) \right. \\ & \left. - \left( M_N -\vphantom{\frac{a}{b}} g_{\sigma} \sigma \right) \right] \psi_{\alpha} + \frac{1}{2}\partial_{\mu}\sigma\partial^{\mu}\sigma - \frac{1}{2}m_{\sigma}^2\sigma^2 \\ & + \frac{\zeta}{4!}g_{\omega}^2(\omega^{\mu}\omega_{\mu})^2 - \frac{\kappa}{3!}(g_\sigma \sigma)^3 - \frac{\lambda}{4!}(g_\sigma \sigma)^4 \\ & + \frac{1}{2}m_\omega^2\omega_{\mu}\omega^{\mu} - \frac{1}{4}W^{\mu \nu}W_{\mu\nu} + \frac{1}{2}m_\rho^2{\rho^\mu}\cdot{\rho_\mu} \\ & - \frac{1}{4}{R^{\mu\nu}}\cdot{R_{\mu\nu}} - \Lambda_\omega g_\omega^2 g_\rho^2 (\omega^\mu \omega_\mu)({\rho^\mu}\cdot{\rho_\mu)} \end{align} \label{eq:lagrangian}\tag{1}\]
Here, \(\psi\) represents the nucleonic Dirac spinor, while \(\sigma\), \(\omega^\mu\), and \(\rho^\mu\) denote the sigma, omega, and rho meson fields, respectively. \(M_N\), \(m_\sigma\), \(m_\omega\), and \(m_\rho\) are the masses of the nucleons and mesons. The parameters \(g_\sigma\), \(g_\omega\), and \(g_\rho\) are the meson coupling constants, whereas \(\kappa\) and \(\lambda\) are the third- and fourth-order self-coupling constants of the scalar meson field. The constants \(\zeta\) and \(\Lambda_\omega\) represent the vector meson self-coupling and the vector-isovector meson coupling, respectively. \(W_{\mu\nu} = \partial_\mu \omega_\nu - \partial_\nu \omega_\mu\) and \(R_{\mu\nu} = \partial_\mu \rho_\nu - \partial_\nu \rho_\mu\) are the field tensors. Finally, \(\tau\) is the isospin operator.
For the leptonic contribution, we consider two leptons in the system: \(e^-\) and \(\mu^-\), and the corresponding Lagrangian contribution is given by,
\[\mathcal{L}_{\text{lep}} = \sum_{k=e, \mu} \bar{\psi}_k (i\gamma^\mu \partial\mu - m_k) \psi_k\]
where \(\psi_k\) and \(m_k\) represent the leptonic Dirac spinor and mass, respectively.
Finally, we add to the Lagrangian the contribution of SIDM by incorporating vector interaction between dark particles as follows [48],
\[\mathcal{L}_{DM} = -g_V\bar{\chi}\gamma^\mu \chi V_\mu - \frac{1}{4}\Phi^{\mu\nu}\Phi_{\mu\nu} + \frac{1}{2}m_V^2 V_\mu V^\mu \label{Ldm}\tag{2}\] where \(V^\mu\) is the vector boson field and \(g_V\) is the DM-vector boson coupling strength. \(\Phi_{\mu\nu} = \partial_{\mu} V_\nu - \partial_\nu V_\mu\) is the field tensor and \(m_V\) is the mass of the vector boson.
Since nucleons, leptons, and DM do not interact with one another, we can write the total Lagrangian for the system as a sum of parts. Thus, the total Lagrangian density is given by
\[\mathcal{L} = \mathcal{L}_{\text{nuc}} + \mathcal{L}_{\text{lep}} + \mathcal{L}_{\text{DM}}\]
Having the obtained Lagrangian density, it is straight forward to derive the expressions for energy density and pressure using the stress-energy tensor.
The energy density corresponding to the nuclear matter is given by,
\[\begin{align} \epsilon_{nuc} = & \sum_{\alpha = n, p} \frac{1}{8\pi^2} \left[k_\alpha E_\alpha^3 + k_\alpha^3 E_\alpha - M^{\star} \ln \left(\frac{k_\alpha + E_\alpha}{M^\star}\right)\right] \\ & + \frac{1}{2}m_\sigma ^ 2 \sigma_0^2 + \frac{1}{2}m_\omega^2 \omega_0^2 + \frac{1}{2}m_\rho^2 \rho_0^2 + \frac{\kappa}{3!} \left(g_\sigma \sigma_0 \right)^3 \\ & + \frac{\lambda}{4!} \left(g_\sigma \sigma_0 \right)^4 + 3\Lambda_\omega\left(g_\rho g_\omega \rho_0 \omega_0\right)^2 + \frac{\zeta}{8}\left(g_\omega \omega_0\right)^4 \end{align}\] where \(k_\alpha\) and \(E_\alpha = \sqrt{k_\alpha^2 + M^{\star^2}}\) are the Fermi momentum and Fermi energy of the \(\alpha^{th}\) nucleonic species respectively. Here \(M^\star\) represents the effective mass of the nucleon and is given by \(M^\star = M_N - g_\sigma \sigma\).
The leptonic contribution to energy density is given by, \[\begin{align} \epsilon_{lep} = & \sum_{i = e^-, \mu^-}\frac{1}{\pi^2} \int_{0}^{k_i} k^2\sqrt{k^2 + m_i^2} \,dk \end{align}\]
The energy density corresponding to the SIDM is given by,
\[\epsilon_{DM} = \frac{1}{\pi^2} \int_{0}^{k_\chi} k^2\sqrt{k^2 + m_\chi^2} \,dk + \frac{1}{2}Gn_\chi^2\] where \(G = \left(\frac{g_V}{m_V}\right)^2\) and \(n_\chi = \frac{k_\chi^3}{3\pi^2}\) represent the self-interaction strength and number density of DM respectively.
Now, we can write the total energy density for DM admixed NS matter as follows,
\[\epsilon = \epsilon_{nuc} + \epsilon_{lep} + \epsilon_{DM}\]
With expression for energy density in hand, the expression for pressure (\(P\)) can be obtained using Gibbs-Duhem relation \[P = \sum_i \mu_i n_i - \epsilon\]
where \(\mu_i\) represents the chemical potential of the \(i^{th}\) species. Chemical potential of the \(\alpha^{th}\) nucleonic species \(\mu_{\alpha}\) is given by, \[\mu_{\alpha} = E_{\alpha} + g_\omega \omega_0 + \frac{1}{2}\tau_{3\alpha}\rho_0\] where \(\tau_{3\alpha}\) is the third component of nucleonic isospin operator. For leptons, the chemical potential is given by, \[\mu_l = \sqrt{k_l^2 + m_l^2}\]
And finally for the DM, the chemical potentials can be derived as follows,
\[\mu_\chi = \sqrt{k_\chi^2 + m_\chi^2} + Gn_\chi\]
In addition to the equilibrium condition resulting from neutron decay into the dark sector, we also assume that the DM-admixed neutron star (DMANS) matter is charge-neutral and in \(\beta\)-equilibrium. These conditions are crucial for accurately modeling NS matter, as they significantly constrain the chemical potentials of the species involved. Therefore, we have the following additional conditions:
\[\begin{align} \mu_n &= \mu_p + \mu_e, \\ \mu_\mu &= \mu_e, \\ n_p &= n_e + n_\mu. \end{align}\]
In this study, we investigate the impact of dark matter on neutron stars by varying the DM self-interaction strength \(G\). As referenced in Ref. [48], the value of \(G\) is constrained within the range \(29.8 \, \text{fm}^2 \leq G \leq 943 \, \text{fm}^2\) based on galaxy cluster observations [59]–[61]. To ensure that the maximum mass of the neutron star remains above \(2 M_\odot\), we begin by fixing \(G = 11 \, \text{fm}^2\) and then vary it up to \(300 \, \text{fm}^2\), with selected values of \(G = 11\), \(15\), \(30\), \(100\), and \(300 \, \text{fm}^2\). Fig. 1 illustrates the pressure-density relationship for different values of \(G\). The plot shows that as \(G\) increases, the effect of dark matter on the EOS diminishes. At lower values of \(G\) (e.g., \(G = 11 \, \text{fm}^2\) and \(G = 15 \, \text{fm}^2\)), the presence of DM significantly softens the EOS, reducing the pressure at a given energy density. As \(G\) increases, the EOS gradually stiffens, with the curve for \(G = 300 \, \text{fm}^2\) closely approaching that of pure hadronic matter (No DM). This behavior indicates that a higher DM self-interaction strength results in a reduced influence of DM on the NS, leading the EOS to resemble that of a neutron star without DM. Consequently, for the purposes of this study, we consider the range of \(G\) values from 11 \(\text{fm}^2\) to 300 \(\text{fm}^2\), as these values cover a broad spectrum of DM effects on the EOS.
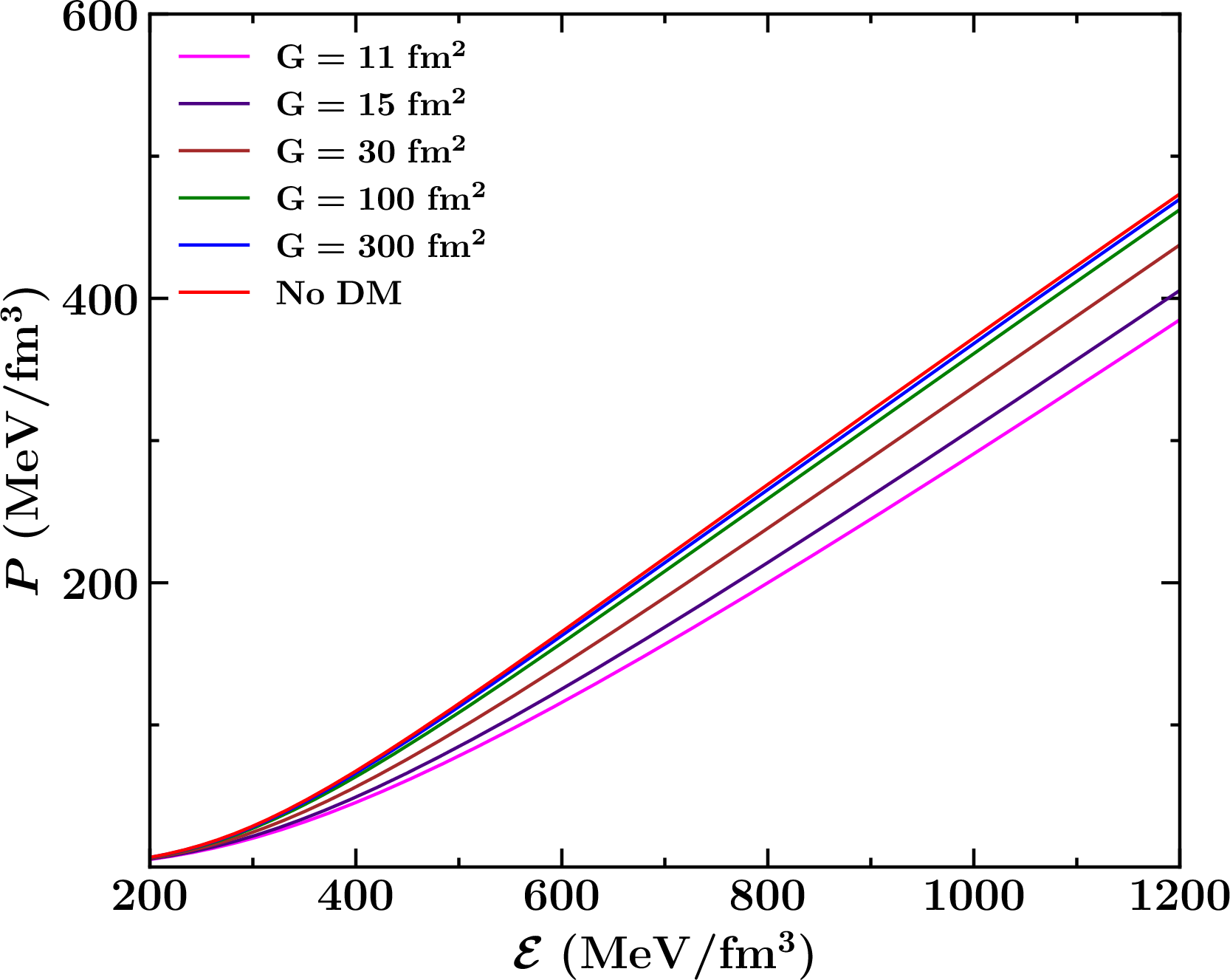
Figure 1: The EOS for DMANS is shown with varying self interaction strength along with without DM.
2.3 Structural Equations↩︎
2.3.1 Static Limit↩︎
The TOV equations, derived from Einstein’s field equations in Schwarzschild-like coordinates, describe the hydrostatic equilibrium of non-rotating neutron stars. These equations are given by \((G = c = 1)\) [10], [11]:
\[\begin{align} \frac{dP}{dr} &= - \frac{1}{r} \frac{(\varepsilon + P)(M + 4\pi r^3 P)}{r - 2M}, \\ \frac{dM}{dr} &= 4 \pi r^2 \varepsilon \, . \label{eq:tov} \end{align}\tag{3}\]
To solve these coupled differential equations numerically, we use boundary conditions: \(m(r=0) = 0\), \(P(r=0) = P_c\); and \(m(r=R) = M\), \(P(r=R) = 0\), where \(P_c\) is the central pressure and \(R\) is the radius of the neutron star. The solution yields the mass and radius of the static neutron star.
In Fig. 2, the mass-radius profiles of DM-admixed neutron stars for various DM self-interaction strengths (\(G\)) are displayed. Each curve represents a different value of \(G\), ranging from \(11 \;{\rm fm^2}\) to \(300 \;{\rm fm^2}\), along with the profile for a purely hadronic star without DM (denoted as ‘No DM’). The plot shows that for all values of \(G\), the corresponding EOS is able to produce a star with a maximum mass exceeding \(2M_\odot\), in agreement with observational constraints such as those from PSR J0952-0607 and PSR J0740+6620. The inclusion of DM, however, leads to a softening of the EOS, which results in a reduction in both the maximum mass and radius of the NS. Specifically, the effect of DM on the mass-radius profile is most significant at lower values of \(G\), such as \(G=11 \;{\rm fm^2}\) and \(G=15 \;{\rm fm^2}\). For these cases, the presence of DM significantly reduces the maximum mass and shifts the curve to the left, indicating a more compact star with a smaller radius. As \(G\) increases, the influence of DM diminishes, with the profile for \(G=300 \;{\rm fm^2}\) closely resembling that of a star without DM. The plot also includes observational data from NICER and XMM-Newton for PSR J0030+0451, showing that all the DM-admixed models considered in this study remain consistent with these observational constraints. Notably, the models with higher values of \(G\) (e.g., \(G=300 \;{\rm fm^2}\)) fall very close to the purely hadronic case, suggesting that the DM effect is almost negligible at these interaction strengths.
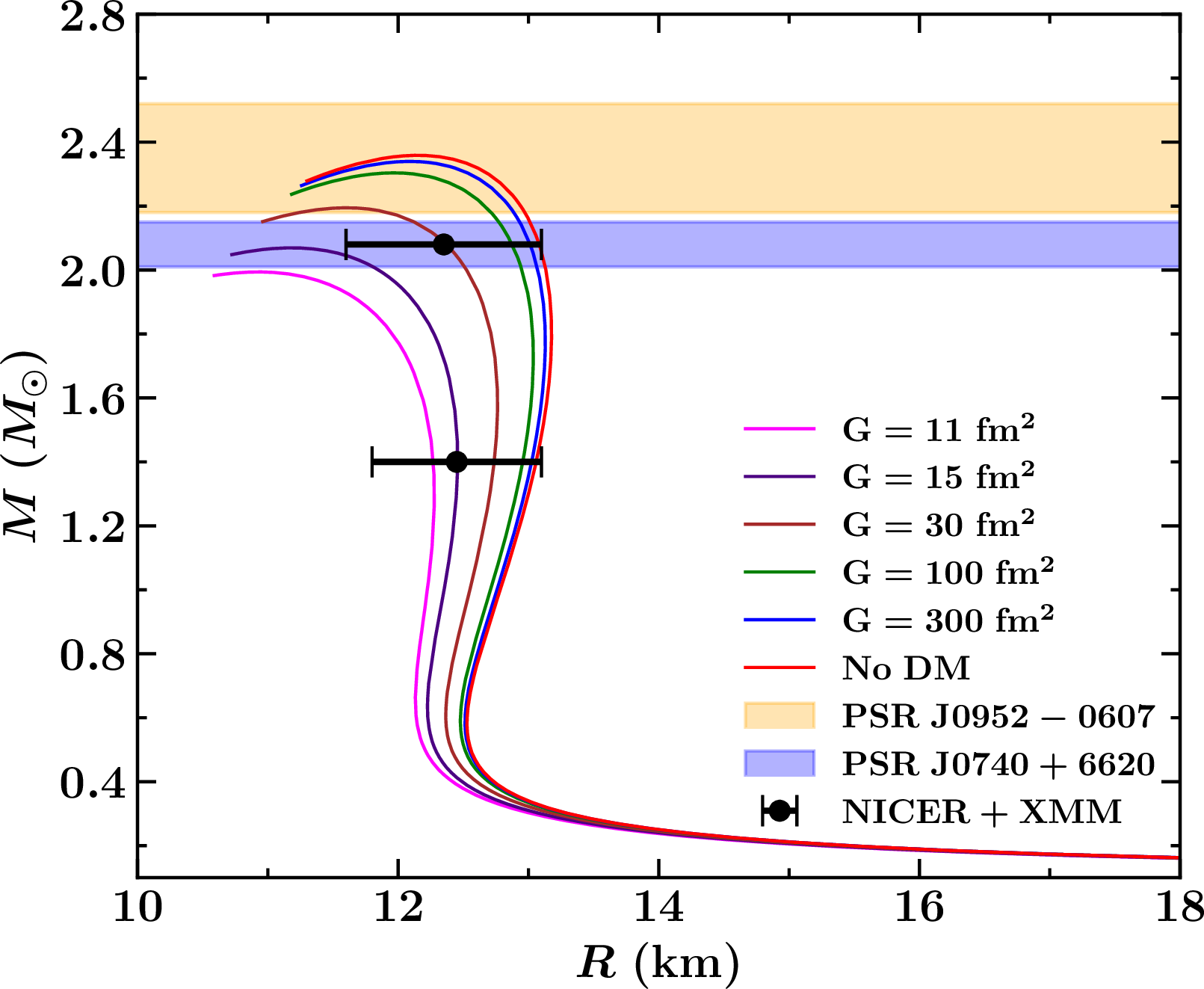
Figure 2: The profile of mass-radius with different strengths of self-interaction is displayed and contrasted with the situation without DM. The error bar indicates the NICER\(+\)XMM constraint [9], and the orange and blue color bands represent the maximum mass constraints by the pulsars PSR J0952\(-\)0607 [62] and PSR J0740+6620 [63], respectively.
2.3.2 Rotating Neutron Star↩︎
The conservation of angular momentum during the core collapse of a high-mass star leads to the rotation of the resulting NS. The rotation of an NS is described using the Hartle-Thorne formalism, which accounts for the effects of rotation on the spacetime metric [12], [13]. For a slowly rotating star, the metric can be expressed as a perturbed Schwarzschild metric [20], [23]. The metric is given by:
\[\label{rns-metric} \begin{align} ds^2 &= -e^{2\varphi}(1 + 2(h_0(r) + h_2(r)P_2(\cos\theta)))dt^2 \\ & \quad + \bigg [1 + \frac{2(m_0(r) + m_2(r)P_2(\cos\theta))}{r - 2M(r)} \bigg ] \bigg [ 1 - \frac{2M(r)}{r} \bigg ]^{-1}dr^2 \\ & \quad + r^2(1 + 2(k_0(r) + k_2(r)P_2(\cos\theta))) \\ & \quad \times [d\theta^2 + \sin^2\theta(d\phi - \omega dt)^2]. \end{align}\tag{4}\]
In this expression, \(h_0(r)\), \(h_2(r)\), \(m_0(r)\), \(m_2(r)\), \(k_0(r)\), and \(k_2(r)\) are perturbation functions that describe the deviations from the Schwarzschild metric due to rotation. \(P_2(\cos\theta)\) denotes the second-order Legendre polynomial, which accounts for the angular dependence of these perturbations. The parameter \(\omega\) represents the angular velocity of the local inertial frame, describing how the star’s rotation affects the spacetime geometry.
Now, one may calculate the relative angular velocity \(\Bar{\omega} = \Omega-\omega\) by solving the following,
\[\label{omegabar} \frac{1}{r^4}\frac{d}{dr}\bigg ( r^4 j \frac{d\bar{\omega}}{dr} \bigg ) + \frac{4}{r}\frac{dj}{dr}\bar{\omega} = 0,\tag{5}\]
using the condition
\[j = j(r) = e^{-\varphi} \bigg [1 - \frac{2M(r)}{r} \bigg ]^{1/2}.\]
Here, for the spherical star having radius \(R\), we can express the angular momentum (\(J\)) as follows,
\[J = \frac{1}{6}R^4\bigg (\frac{d\bar{\omega}}{dr} \bigg ) \bigg |_{r =R}\]
For the rotating star, the perturbed energy density (\(\epsilon\)), pressure (\(p\)) and number density (\(n\)) can be expressed as follows,
\[\begin{align} \label{pertub2} \Delta p = (\epsilon +p)[p_0^* + p_2^*P_2(\cos(\theta)] , \nonumber \\ \Delta \epsilon = (\epsilon +p)[p_0^* + p_2^*P_2(\cos(\theta)](d\epsilon/dp) , \nonumber \\ \Delta n = (\epsilon +p)[p_0^* + p_2^*P_2(\cos(\theta)](dn/dp). \end{align}\tag{6}\]
Now the Einstein’s field equations can be solved to determine the perturbative terms by utilizing the boundary conditions at origin, i.e. \(m_0(0) = p_0^*(0) = h_2(0) = \nu_2(0) = p_2^*(0) = 0\) as follows,
\[\frac{dm_0}{dr} = 4\pi r^2 \frac{d\epsilon}{dp}(\epsilon + p)p_0^* + \frac{1}{12}j^2r^4 \bigg (\frac{d \bar{\omega}}{dr} \bigg )^2 - \frac{1}{3} r^3 \frac{dj^2}{dr} \bar{\omega}^2, \label{dmo}\tag{7}\]
\[\label{dp0} \begin{align} \frac{dp_0^*}{dr} & = - \frac{m_0(1 +8\pi r^2 p)}{(r - 2M(r))^2} - \frac{p_0^* (\epsilon +p)4\pi r^2 }{(r -2M(r))} \\ & + \frac{1}{12} \frac{r^4j^2}{(r - 2M(r))} \bigg ( \frac{d\bar{\omega}}{dr} \bigg )^2 + \frac{1}{3} \frac{d}{dr} \bigg ( \frac{r^3 j^2 \bar{\omega}^2}{r - 2M(r)} \bigg ) \end{align}\tag{8}\]
\[\label{dnu2} \begin{align} \frac{d\nu_2}{dr} & = -2h_2 \bigg ( \frac{d\varphi}{dr} \bigg ) + \bigg ( \frac{1}{r} +\frac{d\varphi}{dr} \bigg ) \bigg [- \frac{1}{3} r^3 \frac{dj^2}{dr} \bar{\omega}^2 \\ & + \frac{1}{6} j^2r^4 \bigg (\frac{d \bar{\omega}}{dr} \bigg )^2 \bigg ] , \end{align}\tag{9}\]
\[\begin{align} \label{dh2} \begin{aligned} \frac{dh_2}{dr} & = -2h_2 \bigg ( \frac{d\varphi}{dr} \bigg ) + \frac{r}{r - 2M(r)} \bigg (2 \frac{d\varphi}{dr} \bigg )^{-1} \\ & \bigg [ 8\pi (\epsilon + p) - \frac{4M(r)}{r^3} \bigg ]h_2 - \frac{4\nu_2}{r(r -2M(r))} \bigg (2 \frac{d\varphi}{dr} \bigg )^{-1} \\ & + \frac{1}{6} \bigg [ \frac{d\varphi}{dr}r - \frac{1}{r -2M(r)} \bigg (2 \frac{d\varphi}{dr} \bigg )^{-1}\bigg ]r^3j^2 \bigg (\frac{d \bar{\omega}}{dr} \bigg )^2 \\ & - \frac{1}{3} \bigg [ \frac{d\varphi}{dr}r - \frac{1}{r -2M(r)} \bigg (2 \frac{d\varphi}{dr} \bigg )^{-1}\bigg ]r^3 \bigg (\frac{dj^2}{dr} \bigg ) \bar{\omega}^2 , \end{aligned} \end{align}\tag{10}\]
\[p_2^* = -h_2 - \frac{1}{3}r^2 e^{-2\varphi} \bar{\omega}^2.\]
Now, the correction in mass can be written as, \[\delta M = m_0 + \frac{J^2}{R^3},\]
and also deformation can be demonstrated as follows,
\[\delta r(r,\theta) = \xi_0(r) + \xi_2(r)P_2(\cos\theta),\]
whereas
\[\begin{align} \label{xis} \xi_0 = -p_0^*(\epsilon + p)\bigg (\frac{dp}{dr} \bigg )^{-1}, \nonumber \\ \xi_2 = -p_2^*(\epsilon + p)\bigg (\frac{dp}{dr} \bigg )^{-1} . \end{align}\tag{11}\]
This allows us to determine the equator’s radius (\(R_e\)) as well as pole’s radius (\(R_p\)) which given by,
\[\begin{align} \label{radii} R_{po} = R + \xi_0 + \xi_2, \nonumber \\ R_{eq} = R + \xi_0 - \frac{1}{2}\xi_2. \nonumber \end{align}\tag{12}\]
Using the above two radii, we can determine the eccentricity of the star as follows, \[e = \sqrt{ 1 - \bigg (\frac{R_{po}}{R_{eq}} \bigg )^2}. \label{ecc}\tag{13}\]
3 Results And Discussions↩︎
In this section, we delve into the combined influence of DM and rotational effects on various NS properties, including central density, mass, radius, and eccentricity. After establishing the Hartle-Thorne formalism, we solve the coupled equations separately for scenarios with and without the presence of dark matter. To comprehensively understand the impact of dark matter, we examine five different interaction strength values, systematically varying the angular velocity for each case.
Before interpreting the results of the rotating NS analysis, it is crucial to first understand how the properties of non-rotating neutron stars relate to the Keplerian frequency. This understanding is key, as determining the Keplerian frequency is essential for identifying the maximum rotational speed that a neutron star can sustain before becoming unstable. The Keplerian frequency serves as a critical parameter, defining the threshold of angular velocity—the mass-shedding limit—beyond which the star would begin to lose mass. For a relativistic star, the Keplerian frequency is expressed as follows [14], [23]:
\[\Omega_k = 0.65 \sqrt{\frac{M}{R^3}}\]
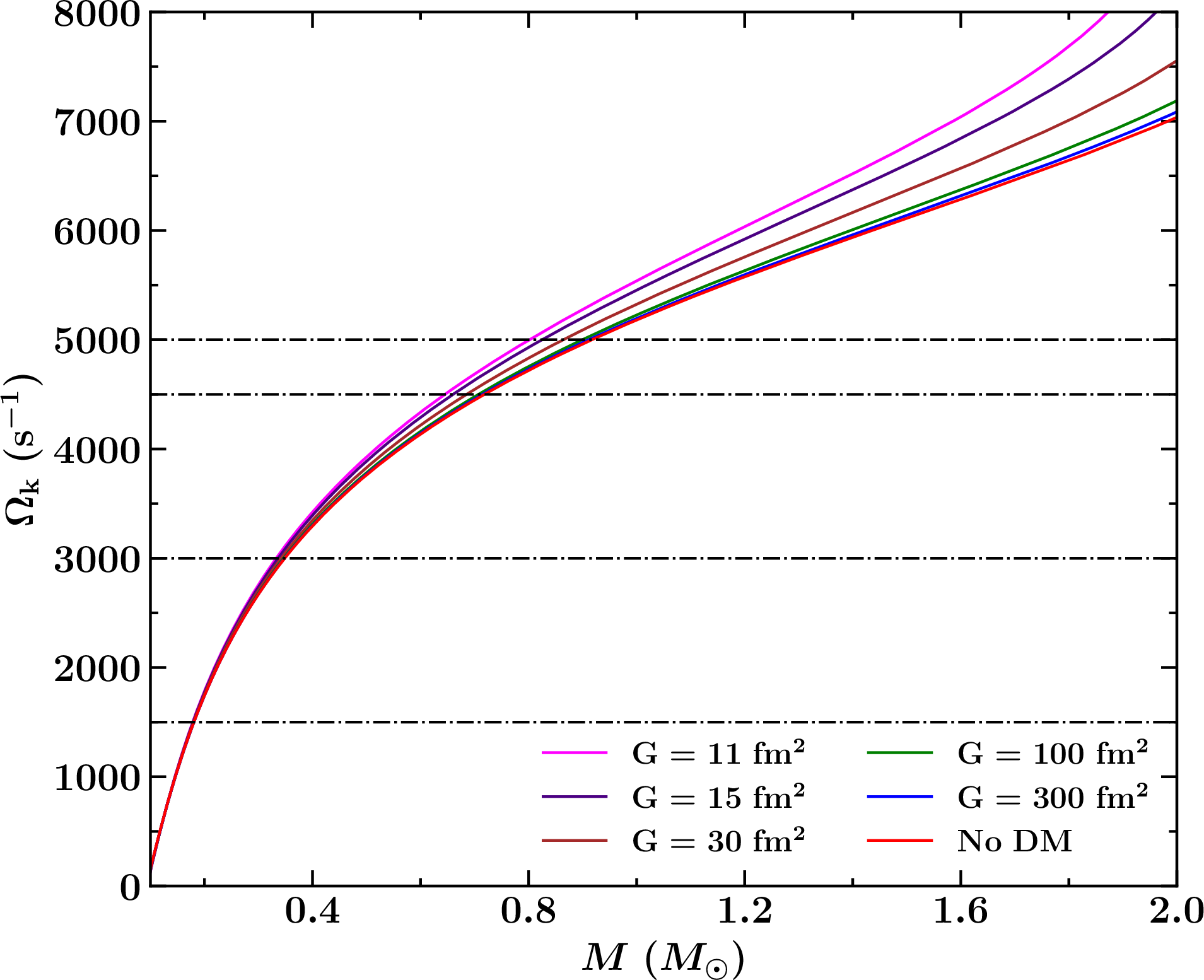
Figure 3: The Keplerian frequency is shown as a function of static mass of the NS at different DM interaction strength.
In Fig. 3, the relationship between the Keplerian frequency (\(\Omega_k\)) and the mass of a static NS is illustrated, highlighting the effects of DM under varying interaction strengths (\(G\)). The plot shows that the presence of DM causes the EOS to soften, which allows the star to reach higher Keplerian frequencies for a given mass. The results indicate that as the DM interaction strength decreases (implying a higher DM content within the star), the Keplerian frequency required to induce mass shedding also increases for a given mass. Specifically, the curves for lower \(G\) values (\(G = 11 \, \text{fm}^2\) and \(G = 15 \, \text{fm}^2\)) are positioned higher, indicating that stars with more DM content require a higher frequency to reach their mass-shedding limit. Conversely, as \(G\) increases, the effect of DM becomes less significant, and the Keplerian frequency approaches that of a star without DM, as shown by the curve for \(G = 300 \, \text{fm}^2\). To further analyze these effects, we selected four angular velocities for our study: \(\Omega = 1500 \, \text{s}^{-1}\), \(3000 \, \text{s}^{-1}\), \(4500 \, \text{s}^{-1}\), and \(5000 \, \text{s}^{-1}\). For each of these angular velocities, we computed the mass-shedding limits under different DM interaction strengths, with the results summarized in Table 1. A key observation is that as the angular velocity increases, the mass-shedding limit also increases, meaning that a faster-rotating star can sustain a higher mass before shedding begins. Regarding DM effects, a lower interaction strength leads to a higher DM content within the NS, which reduces the mass-shedding limit. When comparing the results across all DM interaction strengths, it is evident that for \(G = 11 \, \text{fm}^2\), the mass-shedding limit is the lowest, while for \(G = 300 \, \text{fm}^2\), the mass-shedding limit is the highest, closely resembling the case of purely hadronic matter.
| \(G \;({\rm fm^2})\) | \(\Omega~(s^{-1})\) | \(M_{{\rm lim}}/M_\odot\) |
|---|---|---|
| 11 | 1500 | 0.17 |
| 11 | 3000 | 0.33 |
| 11 | 4500 | 0.64 |
| 11 | 5000 | 0.80 |
| 30 | 1500 | 0.17 |
| 30 | 3000 | 0.34 |
| 30 | 4500 | 0.68 |
| 30 | 5000 | 0.86 |
| 100 | 1500 | 0.18 |
| 100 | 3000 | 0.34 |
| 100 | 4500 | 0.70 |
| 100 | 5000 | 0.89 |
| 300 | 1500 | 0.18 |
| 300 | 3000 | 0.34 |
| 300 | 4500 | 0.71 |
| 300 | 5000 | 0.91 |
| No DM | 1500 | 0.18 |
| No DM | 3000 | 0.34 |
| No DM | 4500 | 0.71 |
| No DM | 5000 | 0.91 |
| \(G\) | \(\Omega\) | \(M_{\mathrm{max}}\) | \(\mathcal{E}_c\) | \(R_{(1.4)}\) | \(e_{1.4}\) |
| \(({\rm fm^2})\) | \({\rm (s^{-1})}\) | \((M_\odot)\) | \({\rm (MeV/fm^3)}\) | \({\rm (km)}\) | |
| 11 | 0 | 1.99 | 1326.1 | 12.26 | 0.0 |
| 11 | 1500 | 1.99 | 1315.8 | 12.34 | 0.13 |
| 11 | 3000 | 2.01 | 1292.72 | 12.56 | 0.27 |
| 11 | 4500 | 2.04 | 1252.07 | 12.98 | 0.40 |
| 11 | 5000 | 2.05 | 1229.41 | 13.17 | 0.45 |
| 15 | 0 | 2.06 | 1256.61 | 12.45 | 0.0 |
| 15 | 1500 | 2.07 | 1251.41 | 12.53 | 0.13 |
| 15 | 3000 | 2.09 | 1225.55 | 12.76 | 0.27 |
| 15 | 4500 | 2.11 | 1184.58 | 13.20 | 0.41 |
| 15 | 5000 | 2.13 | 1164.29 | 13.39 | 0.46 |
| 30 | 0 | 2.19 | 1152.92 | 12.73 | 0.0 |
| 30 | 1500 | 2.20 | 1147.66 | 12.81 | 0.14 |
| 30 | 3000 | 2.21 | 1121.47 | 13.07 | 0.28 |
| 30 | 4500 | 2.25 | 1087.77 | 13.53 | 0.43 |
| 30 | 5000 | 2.26 | 1067.22 | 13.74 | 0.47 |
| 100 | 0 | 2.20 | 1070.93 | 12.95 | 0.0 |
| 100 | 1500 | 2.31 | 1062.96 | 13.04 | 0.14 |
| 100 | 3000 | 2.33 | 1041.82 | 13.30 | 0.29 |
| 100 | 4500 | 2.36 | 1010.4 | 13.79 | 0.44 |
| 100 | 5000 | 2.38 | 989.654 | 14.02 | 0.49 |
| 300 | 0 | 2.33 | 1048.81 | 13.02 | 0.0 |
| 300 | 1500 | 2.34 | 1040.81 | 13.11 | 0.14 |
| 300 | 3000 | 2.36 | 1014.3 | 13.38 | 0.29 |
| 300 | 4500 | 2.40 | 985.442 | 13.88 | 0.44 |
| 300 | 5000 | 2.41 | 975.023 | 14.11 | 0.49 |
| No DM | 0 | 2.35 | 1035.24 | 13.05 | 0.0 |
| No DM | 1500 | 2.36 | 1013.92 | 13.14 | 0.15 |
| No DM | 3000 | 2.38 | 1013.92 | 13.41 | 0.30 |
| No DM | 4500 | 2.42 | 971.79 | 13.92 | 0.44 |
| No DM | 5000 | 2.44 | 971.79 | 14.15 | 0.49 |
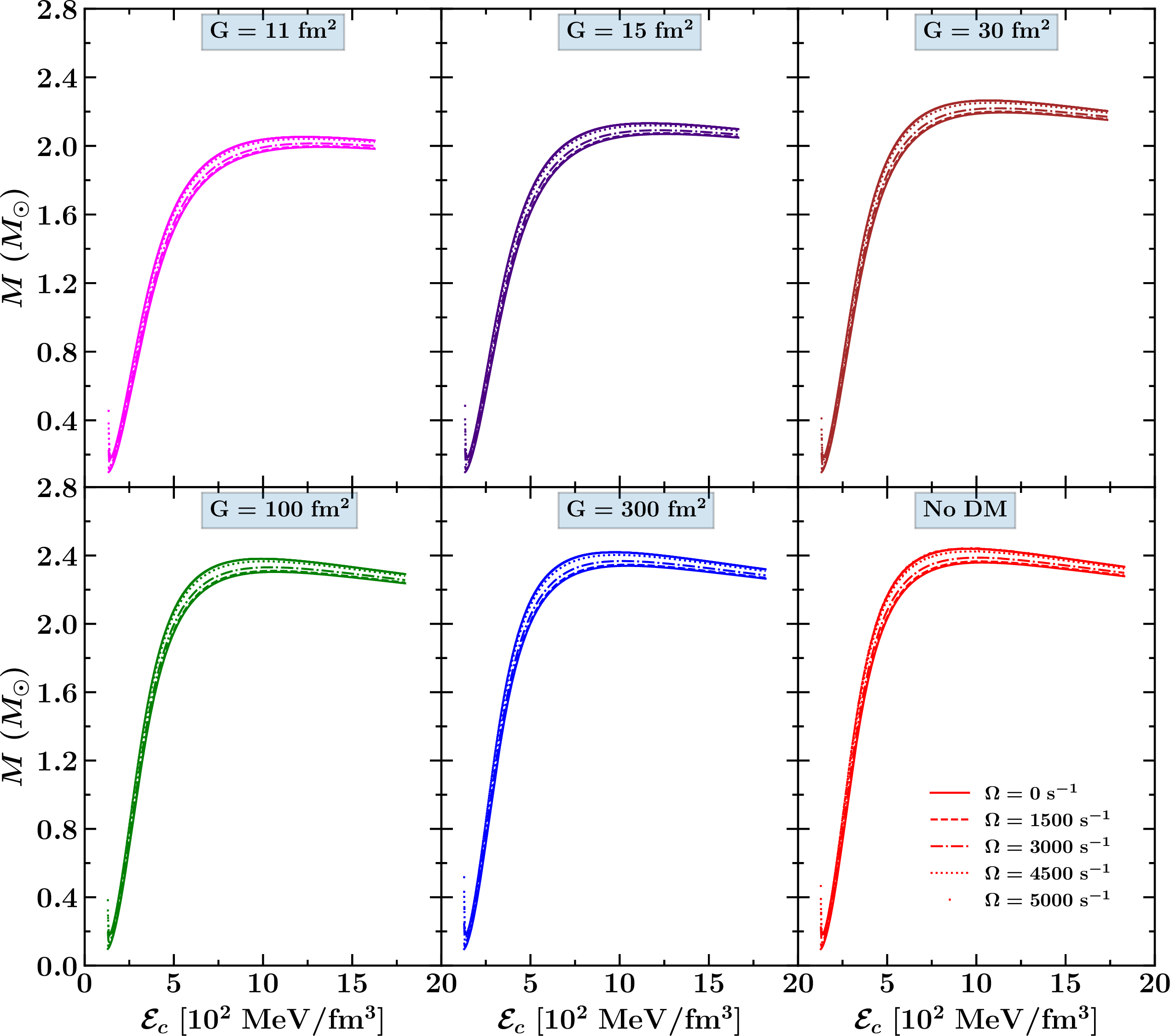
Figure 4: The central density dependency of gravitational mass is shown with combine effect of rotation and DM.
In Fig. 4, we display the relationship between the rotational mass and central density for neutron stars, considering the effects of varying angular velocities and different DM interaction strengths. Each panel illustrates how these parameters influence the mass of the neutron star for a fixed central density. A consistent trend across all panels is that higher angular velocities lead to greater masses for a given central density. This outcome is driven by the centrifugal force generated by rotation, which counteracts gravitational collapse, thereby allowing the star to support a larger mass. In the case of a static star (\(\Omega = 0 \;s^{-1}\)), the star remains spherically symmetric, but rotation causes the star to deform, resulting in a mass correction even at the same central density. The impact of dark matter exhibits an inverse relationship compared to that of angular velocity. As the DM fraction increases, the star’s mass decreases for a given central density. Specifically, at low values of \(G\), such as \(G = 11 \;\text{fm}^2\), the central density at which the maximum mass occurs is higher for both static and rotating stars. This is attributed to the softening of the equation of state due to the presence of DM, which requires a higher central density to reach the maximum mass. Conversely, as \(G\) increases, indicating a reduction in DM content, the central density required to achieve the maximum mass decreases. For the highest value of \(G = 300 \;\text{fm}^2\) and for the No DM case, the central density corresponding to the maximum mass is lower, and the mass profiles for different angular velocities converge closely, reflecting the reduced influence of dark matter.
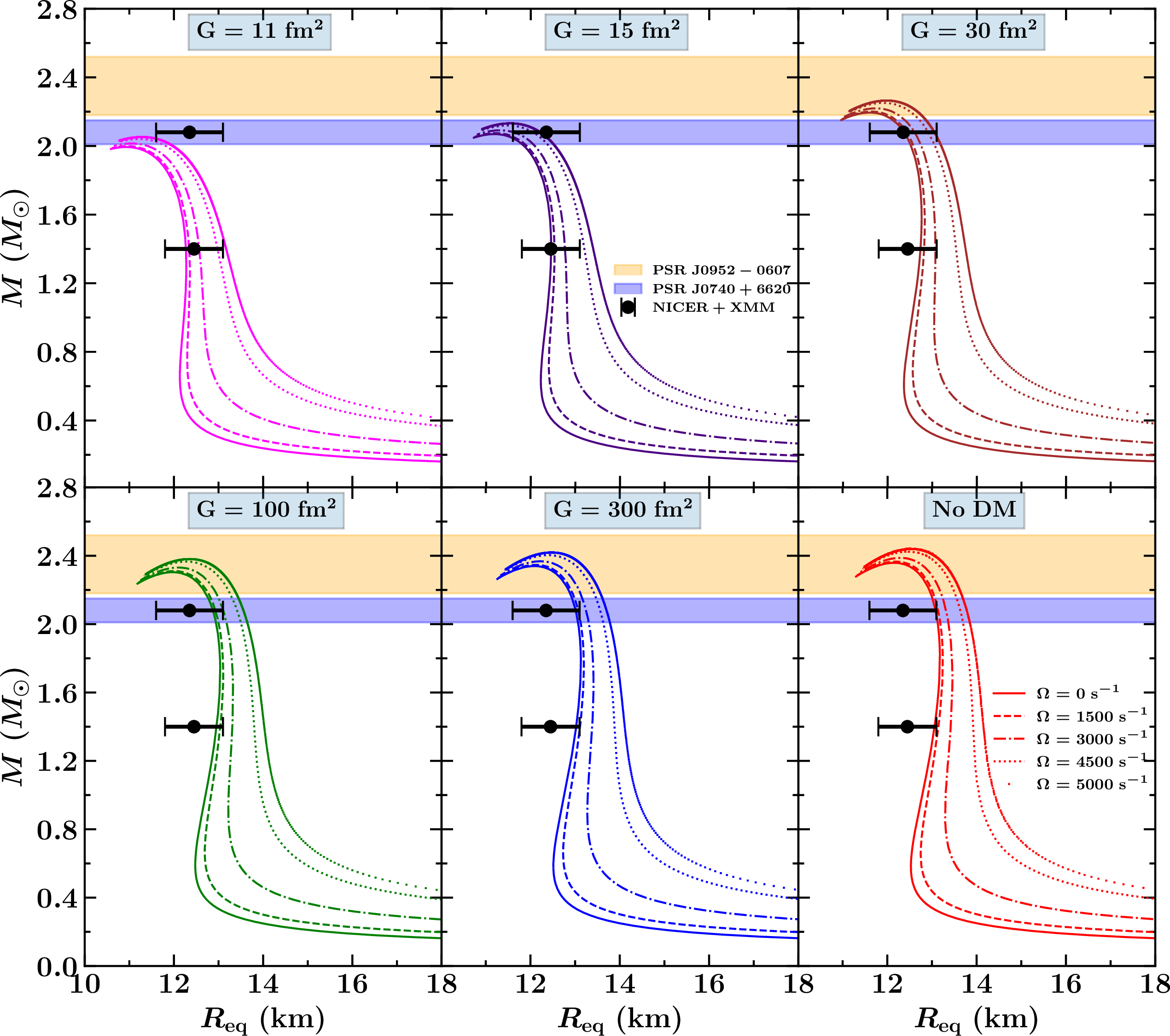
Figure 5: Rotational mass is shown with equatorial radius with varying DM and angular velocities. Mass constraints from different pulsars such as PSR J0952-0607 [62], PSR J0740+6620 [63] are used. The error bar extracting for canonical star and \(2.08 M_\odot\) star from NICER+XMM data for PSR J0740+6620 [9] also used.
To gain a comprehensive understanding of the influence of both DM and rotation on the mass-radius relationship of NSs, we have plotted the rotational mass as a function of the equatorial radius in Fig. 5. Each panel in the figure corresponds to a specific DM self-interaction strength \(G\), while the angular velocities (\(\Omega\)) are varied to examine the properties of DM-admixed NSs. The bottom-right panel represents the mass-radius profile for a neutron star without DM. For the case without DM, the NITR EOS predicts a maximum NS mass of \(2.35M_\odot\) for a static star (\(\Omega = 0 \;s^{-1}\)). As the angular velocity increases to \(\Omega = 5000 \;s^{-1}\), the mass rises to \(2.44M_\odot\), illustrating that rotational effects amplify the difference between static and rotational mass. Simultaneously, the equatorial radius expands from 13.05 km at \(\Omega = 0 \;s^{-1}\) to 14.15 km at \(\Omega = 5000 \;s^{-1}\), which even exceeds the observational constraints provided by NICER and XMM-Newton data. When DM is present, the maximum gravitational mass and radius of the NS decrease, as previously observed in the static mass-radius profile in Fig. 2. This reduction in mass and radius is consistent across all angular velocities. For instance, in the case of \(G = 11 \;\text{fm}^2\), the static star’s mass is \(1.99M_\odot\), which increases to \(2.05M_\odot\) at \(\Omega = 5000 \;s^{-1}\). As the DM interaction strength \(G\) increases, the reduction in mass due to DM becomes less significant, and the values approach those of the no-DM case. Overall, the combination of rotational effects and DM presence leads to a nuanced interplay that significantly affects the mass-radius profile, with detailed results presented in Table 2.
Figure 6 depicts the variation in the canonical radius \(R_{1.4}\) of a NS with a mass of \(1.4 M_{\odot}\) as a function of the DM interaction strength \(G\) for different rotational velocities \(\Omega\). The colored curves represent different rotational velocities, ranging from non-rotating (\(\Omega = 0 \, \text{s}^{-1}\)) to highly rotating (\(\Omega = 5000 \, \text{s}^{-1}\)), and the shaded region corresponds to the observational constraints on the canonical radius from the NICER+XMM data. The figure reveals several key trends. First, in the static case (\(\Omega = 0 \, \text{s}^{-1}\)), the radius \(R_{1.4}\) increases with decreasing DM fraction inside the star, i.e., as \(G\) increases. For \(G = 11 \, \text{fm}^2\), \(R_{1.4}\) is about 12.4 km, but it increases to roughly 13.1 km for \(G = 300 \, \text{fm}^2\). The curve for no DM shows the highest radius, as expected, since the absence of DM results in the stiffest EOS. As the rotational velocity increases, the radius also increases across all DM interaction strengths due to the centrifugal forces that cause the star to expand. For example, at \(G = 11 \, \text{fm}^2\), \(R_{1.4}\) increases from approximately 12.4 km in the static case to around 13.3 km at \(\Omega = 5000 \, \text{s}^{-1}\). A similar trend is observed at all values of \(G\), with the increase in radius becoming more pronounced at higher angular velocities. This increase is consistent with our earlier discussions, where the interplay between rotation and DM was highlighted. Interestingly, as the DM interaction strength weakens (increasing \(G\)), the curves converge, particularly at high rotational velocities. This indicates that at weaker DM interactions (higher \(G\)), the effect of rotation dominates over the DM’s influence on the EOS, leading to similar radii regardless of the DM content. In contrast, at strong DM interactions (lower \(G\)), the DM’s impact on the EOS is significant, resulting in noticeable differences in radius between the static and rotating cases. The shaded NICER+XMM region is particularly informative. At low angular velocities and strong DM interactions (\(G = 11 \, \text{fm}^2\)), the canonical radius lies slightly below the observational constraints. However, as the rotational velocity increases, the radius enters the allowed region, suggesting that moderate rotation can reconcile the predictions with observational data. For weaker DM interactions and no DM, the radius comfortably lies within or even exceeds the observational constraints at higher angular velocities, consistent with the stiffer EOS in these cases.
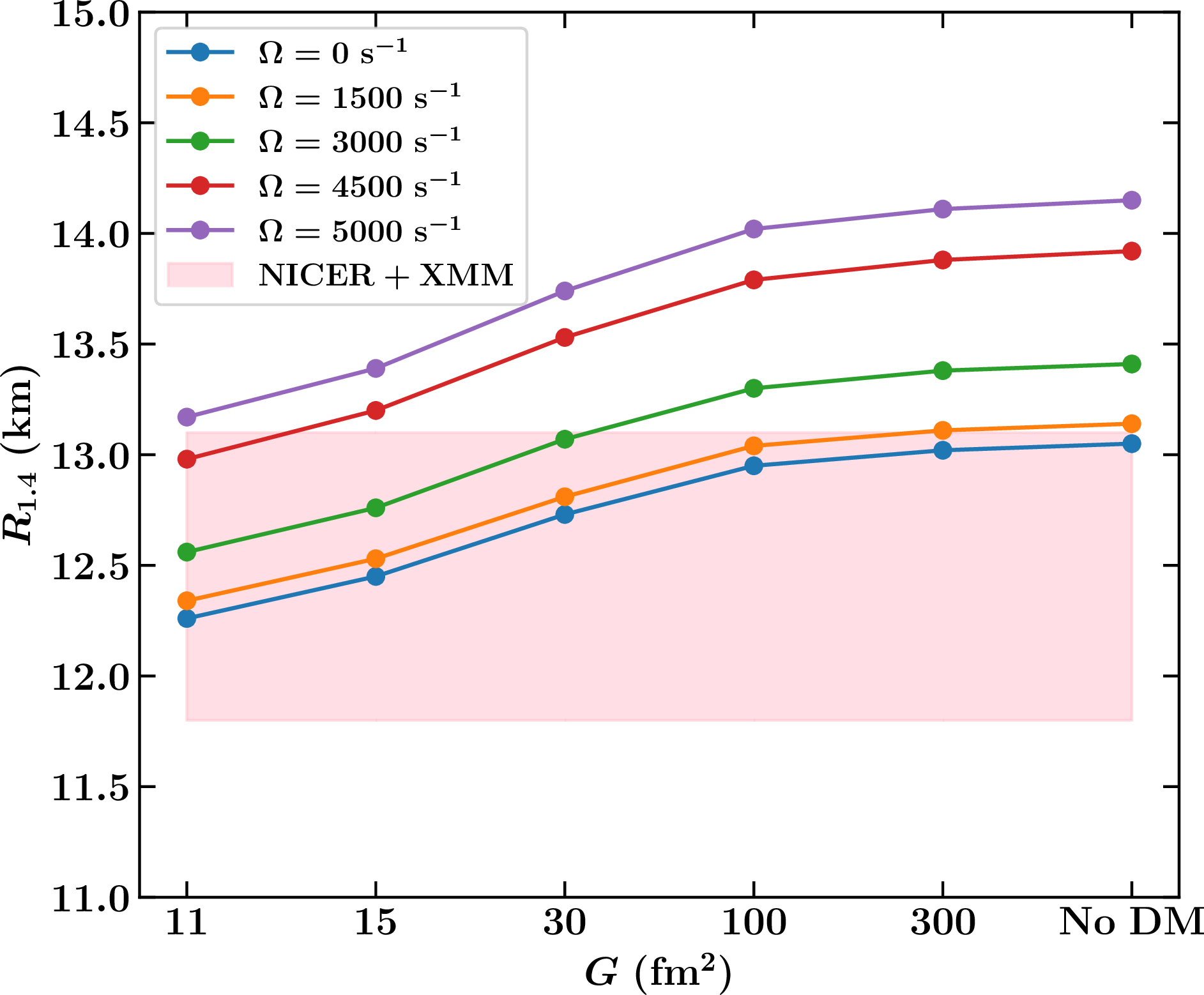
Figure 6: The variation of the equatorial radius corresponding to the canonical mass is shown with the DM interaction strength at different angular velocity.
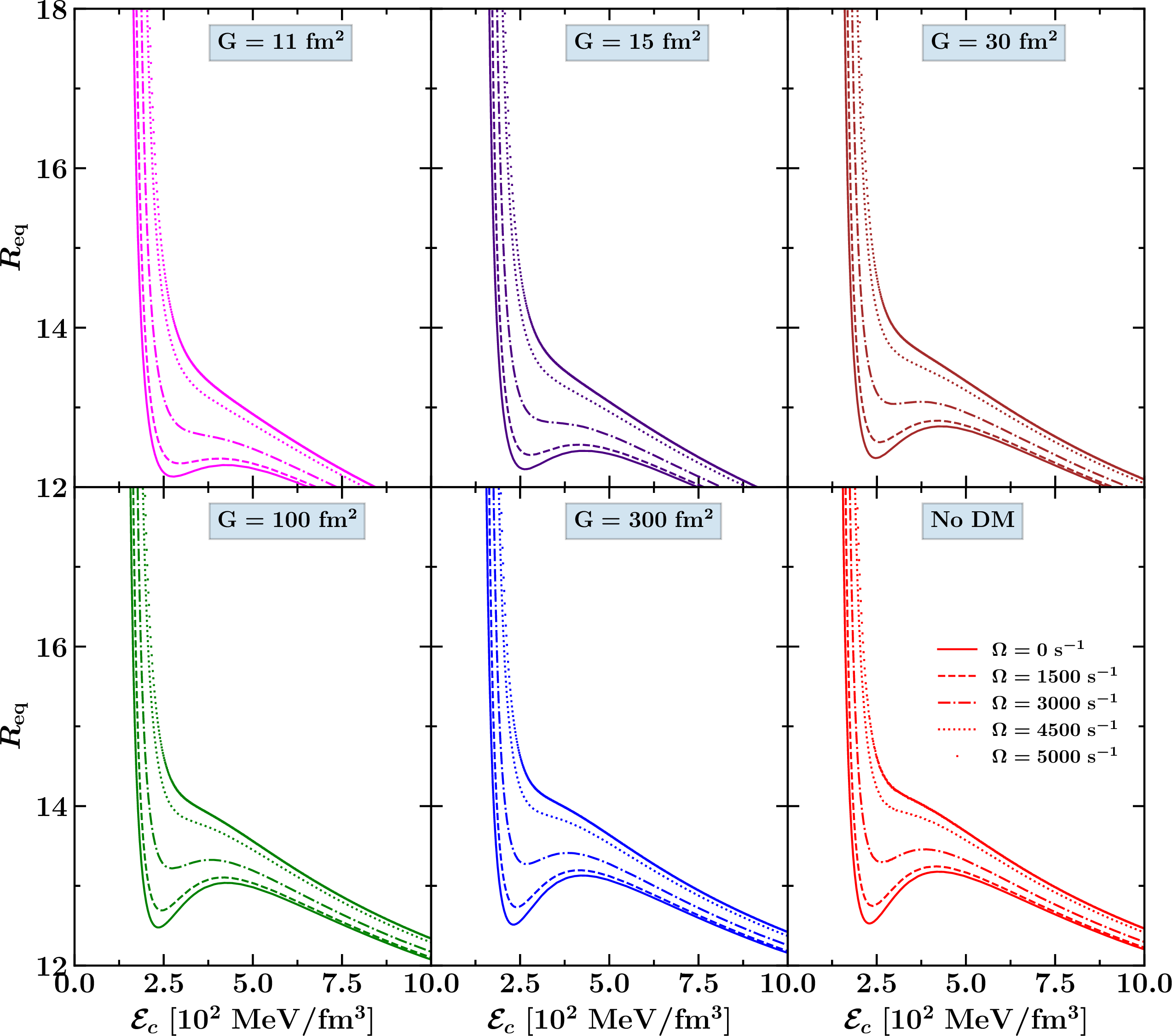
Figure 7: The equatorial radius shown as a function of central energy density with varying angular velocities for DM admixed NS and compared with without DM.
Figure 7 shows the variation of equatorial radius (\(R_{\rm eq}\)) with central energy density (\(\mathcal{E}_c\)) for NSs under different DM interaction strengths (\(G\)) and rotational velocities (\(\Omega\)). Across all panels, it is evident that both DM and rotation significantly influence the star’s structure. For low DM interaction strengths, such as \(G = 11 \;\text{fm}^2\), the presence of DM leads to a more compact star with a smaller equatorial radius. As the central density increases, the radius decreases, indicating a higher compactness. However, as rotational velocity increases, the equatorial radius expands, reducing the compactness and leading to a more deformed star. This trend is consistent across different DM interaction strengths, although the impact of DM diminishes as \(G\) increases. At higher \(G\) values, such as 100 and 300 \(\text{fm}^2\), the effect of DM becomes negligible, and the star’s behavior closely resembles that of a neutron star without DM, where rotation plays a more dominant role. In the absence of DM, shown in the final panel, the equatorial radius decreases with increasing central energy density, resulting in a highly compact star. As the rotational velocity increases, the equatorial radius grows significantly, showcasing the strong influence of rotation on the star’s structure. Comparing the panels, it is clear that while DM generally reduces the equatorial radius and increases compactness, the extent of this effect depends on the interaction strength. Low \(G\) values lead to more compact stars, but as \(G\) increases, the influence of DM weakens, and the star’s properties are primarily governed by rotational effects.

Figure 8: For both DM and without DM case, with varying angular velocities, the eccentricity is plotted with the mass of the NS.
In Fig. 8, the relationship between eccentricity and mass of NSs is analyzed under varying conditions of DM interaction strengths and angular velocities. Eccentricity is a measure of the star’s deformation due to rotation, where \(e = 0\) indicates a perfect sphere, and higher values signify greater deformation, leading to a more oblate shape. Each panel in the figure corresponds to a specific DM interaction strength, allowing us to systematically observe the effects of both rotation and DM on the star’s shape. In the top-left panel, corresponding to \(G = 11 \;\text{fm}^2\), we observe that as the angular velocity \(\Omega\) increases, the eccentricity increases for a given mass, indicating more significant deformation. However, the eccentricity remains relatively low due to the stronger DM interaction, which stabilizes the star against deformation. This trend is consistent across the top row, with \(G = 15 \;\text{fm}^2\) and \(G = 30 \;\text{fm}^2\) showing slightly higher eccentricities for the same mass as DM interaction weakens. The bottom row shows the effects of further reducing DM content. In the case of \(G = 100 \;\text{fm}^2\) and \(G = 300 \;\text{fm}^2\), the eccentricity increases more sharply with mass, reflecting a star that becomes significantly more oblate at higher rotational velocities due to the weaker DM interaction. The final panel, showing no DM, demonstrates the maximum eccentricity observed across all cases, confirming that DM plays a crucial role in reducing rotational deformation.
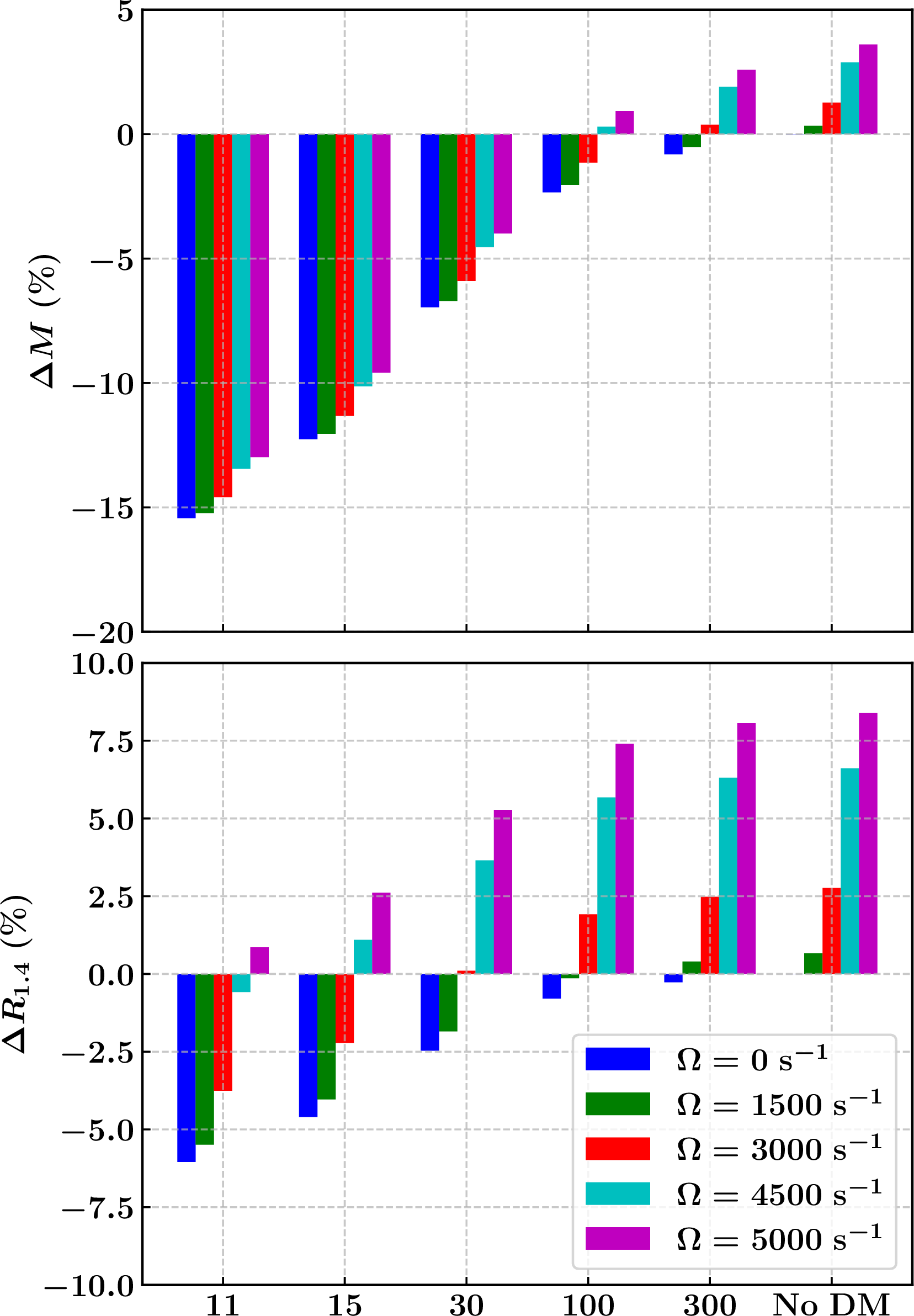
Figure 9: The relative deviation for maximum mass (\(\Delta M\)) and canonical radius (\(\Delta R_{1.4}\)) under the influence of both DM and rotation is shown.
Analyzing Table 2 reveals that the interplay between rotation and DM can either increase or decrease NS properties relative to their standard, non-rotating, and DM-free configurations. To elucidate these effects, we calculated the relative deviation of NS properties from their baseline values and depicted these deviations in Fig. 9. The top panel highlights deviations in maximum mass (\(\Delta M\)), where, in the non-rotating case (\(\Omega = 0 \, {\rm s^{-1}}\)), the maximum mass deviates up to about 16% below its standard value, with more significant deviations at higher DM interaction strengths. When rotation is introduced, these deviations decrease with higher angular velocities. At the highest angular velocity considered (\(\Omega = 5000 \;{\rm s^{-1}}\)), the deviation reduces to around 13%. As the interaction strength \(G\) increases, reducing the DM content in the star, the relative deviation in maximum mass shifts from negative to positive at \(G = 100 \, \text{fm}^2\) and \(\Omega = 4500 \;{\rm s^{-1}}\), suggesting that under these conditions, the rotating DM-admixed NS’s maximum mass can exceed its baseline value. Conversely, at higher DM fractions (\(G = 300 \, \text{fm}^2\)), the maximum mass initially decreases at lower angular velocities, but as rotation intensifies, the deviation turns positive, continuing this trend even in the absence of DM. The bottom panel of Fig. 9 presents the relative deviation in the canonical radius (\(\Delta R_{1.4}\)), which mirrors the mass deviation trends. In the static case with DM, \(\Delta R_{1.4}\) initially decreases, but the magnitude of this decrease diminishes with higher rotational speeds. As the DM fraction decreases and rotation increases, the deviation in \(\Delta R_{1.4}\) eventually becomes positive, indicating greater deformation of the star.
4 Summary And Conclusions↩︎
In this study, we systematically explored the combined effects of DM and rotation on NS properties using the NITR equation of state. We have focused on analyzing mass, radius, eccentricity, and compactness under varying conditions of DM interaction strength and rotational velocity. The findings highlight the intricate interplay between these factors, demonstrating their combined effects on the structural properties of NSs.
Our results indicate that both DM and rotation significantly influence NS mass and radius. Rotation, driven by increasing angular velocity, generally leads to an expansion of the equatorial radius and an increase in mass due to centrifugal forces. For example, in the absence of DM, the NITR EOS predicts a maximum NS mass of \(2.35M_\odot\), which rises to \(2.44M_\odot\) at \(\Omega = 5000 \, \text{s}^{-1}\), with the equatorial radius extending from 13.05 km to 14.15 km. However, this rotational expansion pushes the radius beyond the observational constraints set by NICER+XMM data. When DM is introduced, it exerts a stabilizing effect, particularly at higher DM fractions (lower interaction strengths, such as \(G = 11 \, \text{fm}^2\)), leading to a reduction in both the maximum mass and radius. For instance, with \(G = 11 \, \text{fm}^2\), the maximum mass drops to \(1.99M_\odot\) for a static NS and to \(2.05M_\odot\) at \(\Omega = 5000 \, \text{s}^{-1}\).
Eccentricity, a measure of rotational deformation, increases with angular velocity but decreases with higher DM content, reflecting DM’s role in reducing deformation and maintaining a more spherical shape. Compactness, defined as the ratio of mass to radius, generally decreases as DM content increases or as rotational velocity rises, further illustrating DM’s mitigating influence on deformation. Additionally, we assessed the relative deviations in maximum mass (\(\Delta M\)) and canonical radius (\(\Delta R_{1.4}\)) from their baseline values. The largest reduction in \(\Delta M\) (approximately 16%) occurs at high DM fractions and low angular velocities, whereas low DM fractions combined with high angular velocities result in an increase in \(\Delta M\). A similar trend is observed for \(\Delta R_{1.4}\), where the deviation becomes positive at high rotational speeds and low DM content, indicating significant deformation.
Overall, the study confirms that the combined effects of DM and rotation lead to significant deviations in NS properties from their true values, underscoring the complex relationship between these factors. The mass range predicted by the NITR EOS aligns with the observed maximum mass of PSR J0952-0607, particularly for cases with moderate DM interaction strengths (\(G = 30 \, \text{fm}^2\), \(100 \, \text{fm}^2\), \(300 \, \text{fm}^2\)) and without DM. However, satisfying the NICER+XMM radius constraints requires careful consideration of both DM content and rotational velocity, highlighting the need for precise modeling when evaluating NS properties under different physical conditions.
Acknowledgements↩︎
B.K. acknowledges partial support from the Department of Science and Technology, Government of India with grant no. CRG/2021/000101.