Synthetic Data for Robust Stroke Segmentation
April 02, 2024
1 Introduction↩︎
classification of images or volumes, known as semantic segmentation, is crucial in many neuroimaging and medical imaging analysis pipelines. Properties such as volume and surface distance of healthy tissue structures are used in longitudinal models to measure anatomical changes, while tumor labels are essential for radiotherapy planning. Extracting fine-grained labels has typically been limited to high-contrast, high-resolution structural scans, such as those acquired using the MPRAGE sequence, which are rarely found in clinical settings. This limitation poses a significant barrier to applying these methods in clinical practice.
Both traditional probabilistic methods [1] and modern deep discriminative methods [2] require prior information to be provided for a given sequence - in the case of a traditional method this may be an atlas or template, and in modern methods this would come in the form of training data. Atlas-based methods build a template of the anatomical structure of the brain, which may be deformed into alignment with a new subject to assign voxel-wise anatomical classes. This is proven to be robust for delineating healthy structure even with shifts in contrast [3], however it is non-trivial to include classes of pathology such as stroke within such a model, due to the inherent heterogeneity in location and geometric properties. In the context of generative models, lesions may be included in the form of anomaly detection as demonstrated in [4]. This method is not however directly attempting to label the pathology, and (by design) will label physiological changes such as ventricular enlargement in addition to the responsible infarct.
Deep discriminative models trained using supervised learning have been able to reach human-level performance when tested in-domain on large datasets for a variety of brain pathologies and imaging modalities [5], [6]. There is still however a significant gap when trying to translate these models to clinical data, where each hospital is likely to vary both in the scanning equipment used and the choice of imaging sequences [7]. This poses a significant challenge to the adoption of deep learning for automating the labelling of clinical data, which could greatly help to accelerate the translation of modern research in stroke prognosis [8].
To extend such methods to the open-ended domain of clinical scans, models often need to perform on sequences for which no training data may be available. To this end, domain randomisation via synthetic data has been shown to give impressive results for healthy brain parcellation in SynthSeg [9]. In this method, a set of ground truth healthy tissues are used to generate synthetic images, under the assumption that each tissue class’ intensity distribution should roughly follow a Gaussian. By assigning random Gaussian distributions to each class, a deep learning model can learn to extract shape information for parcellation in a way that is invariant to the input image’s relative tissue contrast, hence allowing the model to be used on any sequence at test-time, without training data or prior knowledge of the sequence. This method of training with synthetic data has since been extended to tasks such as image registration [10]–[12], image super-resolution [13], [14], surface estimation [15], [16] and vascular segmentation [17]. A comprehensive overview is available in [18].
An additional benefit of this method is that the ‘forward model’ of creating an MRI (or CT) image from tissues of different physical properties is a perfect 1:1 mapping to the ‘inverse model’ of labeling the tissues (i.e. segmentation) from the acquired image. In structures that exhibit a large amount of inter-rater variability, this is likely to help prevent a model from imitating under- or over- segmentation from imperfect ground truths - the images segmented are generated from the corresponding segmentation labels and so labels will always be a consistent method of segmentation.
Prior work to SynthSeg demonstrated the potential of encoding anatomical priors in a neural network through pre-training with unpaired parcellation labels [19]. Such methods face significantly larger challenges when applied to the heterogeneous shape and spatial distribution of lesions. In healthy parcellation, anatomical structures have consistent positions across individuals (e.g., the brainstem reliably appears in the same region of the brain), a regularity that has motivated atlas-based approaches to parcellation. In contrast, lesions are highly variable across individuals—not only in number and size but also in their spatial distribution. Unlike anatomical structures, lesions cannot be reliably mapped to a specific location or shape within an atlas. Although the exact site of lesion initiation is often influenced by the brain’s vascular architecture—meaning that certain regions are statistically more susceptible to stroke due to the location of large blood vessels—the resulting lesion’s size, shape, and spread are highly variable. Multiple sclerosis serves as an exception, with lesions that are somewhat predictable in their white matter localisation [20], enabling modelling through synthetic deep learning frameworks [21] and traditional probabilistic models [22]. More recently, [23] has shown promising results by training a SynthSeg-like model on lesion labels from various pathologies, providing a foundation for fine-tuning on multiple downstream datasets. However, achieving a model that can seamlessly generalise for open-domain stroke segmentation remains an active area of research
In our work, we extend the SynthSeg framework to the task of stroke lesion segmentation via a novel lesion-pasting method that better simulates variety in lesion appearance. We show that this can be used to expand an existing segmentation dataset to attain competitive performance in-domain, and state-of-the-art performance out-of-domain that can be further enhanced with existing test-time domain adaptation techniques. We validate this on a comprehensive range of lesion datasets with a wide distribution of image characteristics and lesion physiology. To assist in widespread evaluation of this framwork, we release PyTorch training code/weights, and a MATLAB toolbox for SPM to reduce the barrier to clinical adoption.
2 Methods↩︎
The core premise of our training procedure is to generate synthetic images with paired labels by combining random permutations of healthy tissue labels and binary stroke lesion maps.
A number of important modifications were made from the original SynthSeg procedure to better suit it to the task of stroke segmentation. First, as we are ultimately only interested in annotating stroke infarct and not the surrounding anatomy, we can opt for a much simpler set of labels than the full set of anatomical labels generated from Freesurfer in SynthSeg. For our experiments we opt for the posterior maps generated using the MultiBrain toolbox in SPM [24]. This reduces the number of sampled healthy labels to only 9 classes, and requires using a single model to generate labels instead of the two used in SynthSeg. A comparison of the sampled labels from Freesurfer and MultiBrain can be seen in Figure 1. Sampled labels are summed using a weighting based on their posterior likelihoods, allowing for the simulation of partial volume. Of these classes, only 4 are labels of brain tissue (Gray Matter (GM), White Matter (WM), GM/WM partial volume and Cerebrospinal Fluid (CSF)) which also makes for a lower memory footprint in training. In all Synth-model training, we opt for predicting these 4 tissue classes in addition to the lesion class in order to prevent issues of class imbalance that can occur when treating lesion segmentation as a binary task.
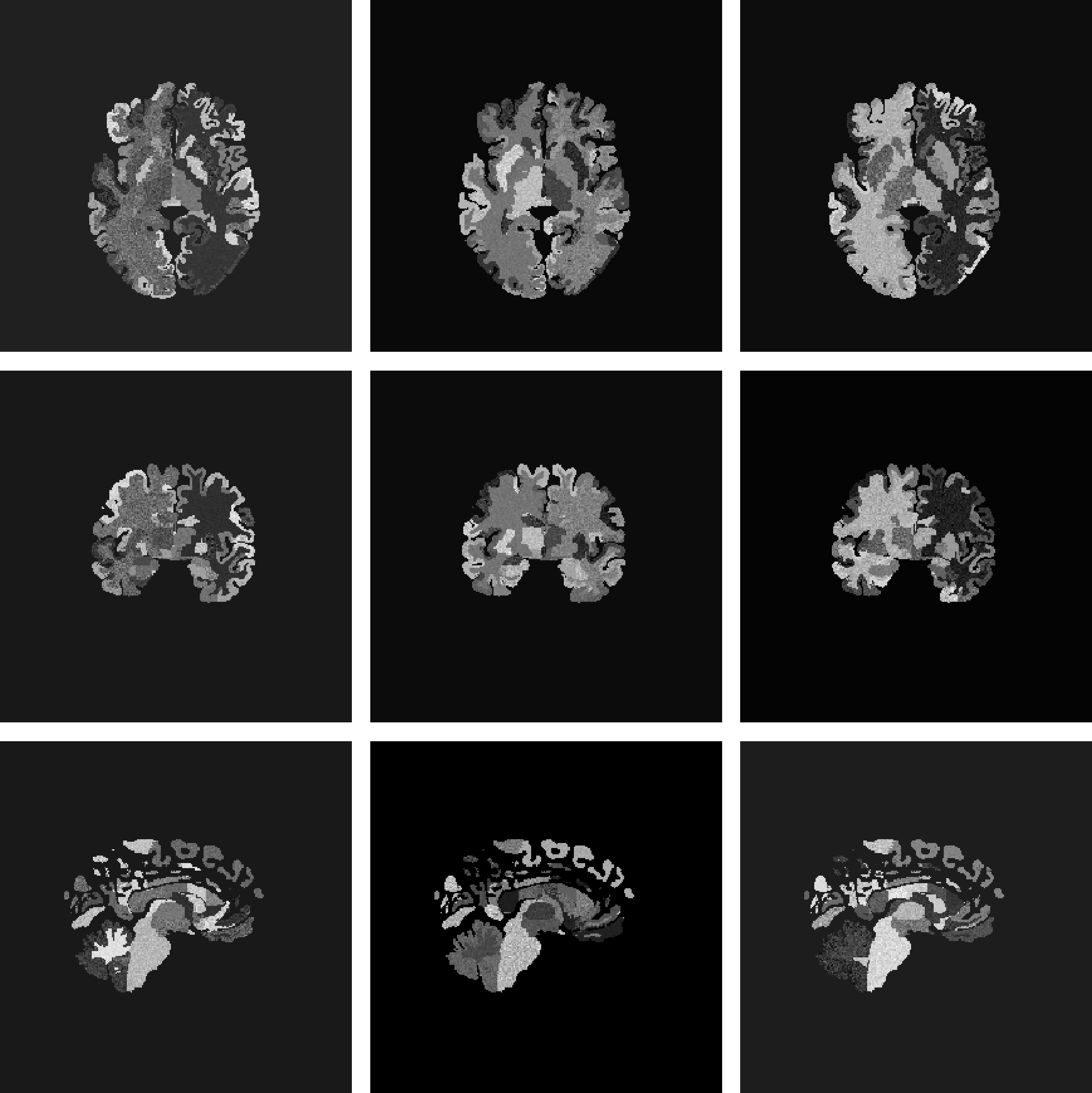
Freesurfer [3]
MultiBrain [24]
MultiBrain (skull-stripped)
Figure 1: Sample generated images using different labels for a single subject. 1 (a): Freesurfer anatomical labels. 1 (b): MultiBrain tissue labels. 1 (c): MultiBrain tissue labels masked to simulate skull-stripping..
We also enhance the default training procedure by introducing lesion-specific augmentations to mimic variability in lesion appearance. We first use the Soft-CP algorithm [25] with random dilations and erosions to vary how the infarct is blended into its neighbouring healthy tissue. We also introduce a spatially varying multiplicative field to the binary lesion map, which mimics the variety in the local texture of a lesion and presence of penumbra within a stroke. This is performed by applying the MONAI Random Bias Field augmentation [26] and thresholding the result in the \([0,1]\) range. A similar approach was adopted in [27] and showed in improvement in model sensitivity.
A model was trained using a combination of healthy labels from the OASIS-3 dataset [28] and lesion masks from the ATLAS dataset [29]. In the OASIS-3 dataset (N=2679, 2579:100 train-val split), tissue labels were extracted using SPM’s MultiBrain [24] and spatially aligned to ICBM space to enable correct lesion placement. The ATLAS dataset (N=655, 419:105:131 train-val-test split) was used for pasting lesion maps, which were also aligned to ICBM space. A lesioned brain map was generated by randomly pasting an ATLAS lesion label onto an OASIS subject’s parcellation using the previously described augmentations.
The generated maps were used to randomly assign Gaussians to each tissue class by sampling a mean from the distribution \(\mu \sim \text{Uniform}(0,255)\), a standard deviation \(\sigma \sim \text{Uniform}(0,16)\) and the FWHM of the applied smoothing from \(\text{Uniform}(0,2)\). All images were then extensively augmented using a variety of transformations. These include the application of a random bias field, which involves rescaling intensities based on a smooth multiplicative field controlled by a number of control points \(\mathcal{U}(2,7)\) and a bias strength \(\mathcal{U}(0,0.5)\), with multiplicative values sampled from \(\mathcal{U}(1-\text{strength}, 1+\text{strength})\). Random affine deformation is also employed, consisting of random rotations within \(\mathcal{U}(-15,15)\) degrees, shearing within \(\mathcal{U}(0,0.012)\), and zooming within \(\mathcal{U}(0.85,1.15)\). Additionally, random elastic deformations are applied with a maximum displacement \(\mathcal{U}(0,0.05)\) using control points \(\mathcal{U}(0,10)\). Another transformation simulates random skull-stripping by generating a perfect foreground mask of brain tissues and introducing flaws through random dilation (probability of 0.3, radius of 2) and erosion (probability of 0.3, radius of 4). Random flips are applied across each axis with a probability of 0.8. Random Gaussian noise is introduced, controlled by a signal-to-noise ratio (SNR) \(\mathcal{U}(0,10)\), and smoothed by a g-factor field with smoothness \(\mathcal{U}(2,5)\). Slice anisotropy is simulated by rescaling the slice thickness based on a resolution factor \(\mathcal{U}(1,8)\), with experiments assuming an original isotropic resolution of 1mm\(^3\). Random contrast adjustment is applied using a gamma factor \(\gamma\) sampled from \(10^{\mathcal{N}(0,0.6)}\), while random motion blurring is simulated using a point-spread function with a full width at half maximum (FWHM) \(\mathcal{U}(0,3)\). Intensities were clipped to the 1st and 99th percentiles and images z-normalised to a zero mean and unit standard deviation. Training was performed at an isotropic spacing of 1 mm and volumes randomly cropped to 192\(\times\)192\(\times\)192. A simplified schematic (with image-quality augmentations removed) is shown in Figure 2.
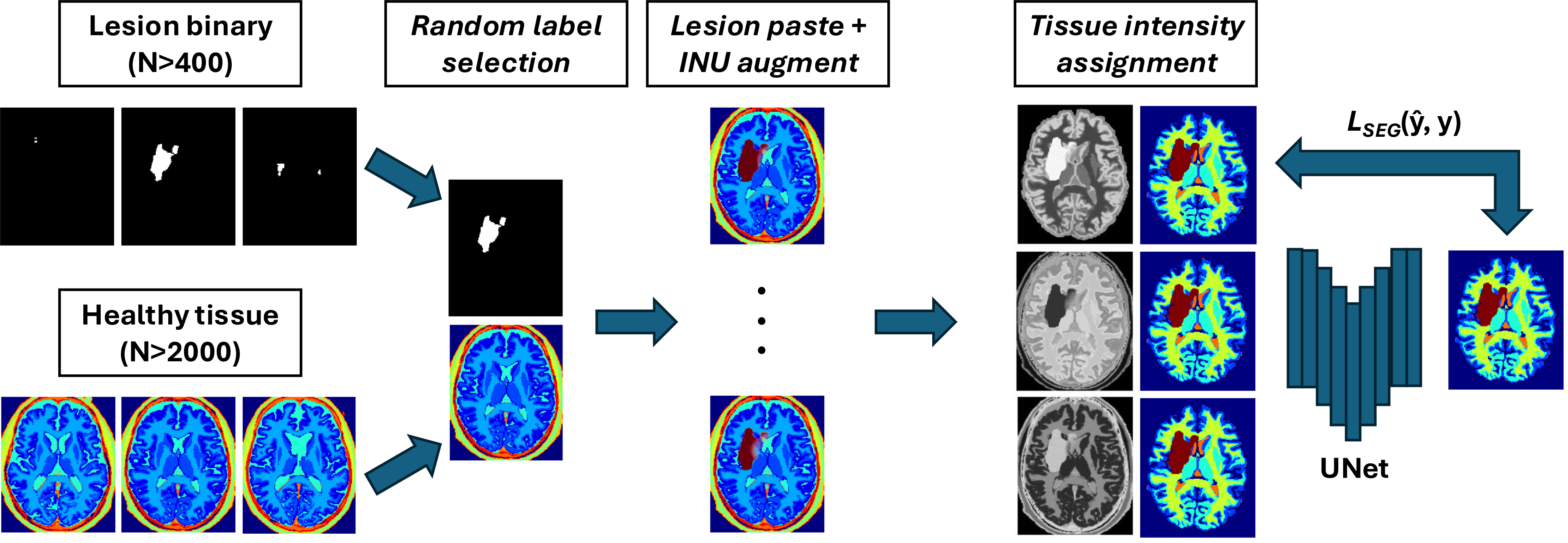
Figure 2: Schematic overview of the data generation process. Lesions are sampled from a template-normalised bank of lesion binary masks, and healthy tissue maps are sampled from a template-normalised bank of MultiBrain segmentations. Pasting of lesions onto healthy tissue maps is performed using a spatially varying lesion intensity to simulate penumbra. Tissue intensities may then be sampled from Gaussian distributions and image-label pairs used to train a segmentation model in a supervised manner.
For the synthetic model (labeled Synth in all experiments), a combination of real and synthetic data was used for training. Real data was sampled from the ATLAS dataset (using the same training split from which lesion labels were derived). Real MPRAGE images were augmented with random cropping to 192\(\times\)192\(\times\)192, random affine and elastic deformations, histogram normalization, random histogram shift, random field inhomogeneity, random gamma contrast adjustment, and random flipping in all axes, before being z-normalized to zero mean and unit standard deviation. The real and synthetic data loaders were rotated in a weighting based on the number of images present (2579:419 in training for synthetic and real images respectively). In the baseline model (labeled Baseline in all experiments), only the real data loader was used with identical transforms, while all other training aspects were kept constant.
A UNet architecture [30] was used for this task with the specification used in nnUNet [2] including 6 encoder/decoder stages with output channels \((16,32,64,128,320,320)\), with changes to use PReLU activation [31] and one residual unit per block [32]. Six output channels were predicted from the network, covering background, the four healthy MultiBrain tissues (gray matter (GM), white matter (WM), gray/white matter partial volume (PV), cerebro-spinal fluid (CSF)) and the stroke lesion class. In the baseline model, only the background and stroke lesion classes were predicted. In the case of mixed real/synthetic data, the real images’ binary ground truth was treated as a partial ground truth label and loss was only calculated for the stroke lesion class of the prediction. Training was always performed using a single input channel, due to the desire for the model to be generally applicable to any number of available modalities. We propose a naive method for ensembling all available modalities for a subject in Section 3.
Training minimised a combined Dice and Cross Entropy loss. An AdamW optimiser [33] was used with a learning rate of \(10^{-4}\) and a decay of \(0.01\), using a scheduler of \(\eta_{n} = \eta_{0}(1 - \frac{n}{N})^{0.9}\) for a learning rate \(\eta\) at step \(n \in \{1,...,N\}\), adapted from nnUNet [2]. Gradient clipping was applied for a norm value of 12 to ensure stability [34]. A dropout of 0.2 was used during training. Models were trained using a batch size of 1 for 1200 epochs, each of 500 iterations (total \(6\times10^5\) iterations).
2.1 Domain Adaptation↩︎
At test-time, we evaluate the utility of a wide range of unsupervised domain adaptation techniques to see if (a) the baseline model could match the Synth model performance with a modern DA method and (b) if the robustness of the Synth model could provide a better starting point for DA to optimise on the new domain. The first of these to be used (referred to in results as ‘TTA’) is test-time augmentation (TTA) [35]. TTA is a popular heuristic for improving robustness of models in out-of-domain (OOD) scenarios and is expected to provide a free improvement on all models’ robustness with little risk of corrupting predictions.
The second method to be used (referred to in results as ‘DAE’) was the Denoising Autoencoder (DAE) method proposed in [36]: for both the single-label baseline and multi-label Synth model, DAE models were trained to perform cleanup of noise in labels. This method relies on learning to regularise labels to a learned spatial distribution, such that the difference in the before and after of this regularisation can provide an estimate of label degradation. At test-time, a small series of normalisation layers are prepended to the segmentation model to manipulate the input intensities. This consists of 3 convolution layers with kernel size of 3 and with 16 channels, each followed by a custom activation:
\[f(x) = \exp{-\frac{x^2}{\sigma^2}},\]
where the scale factor \(\sigma\) is a learned parameter as described in the original paper. For each image at test-time, this normalisation network is re-initialised and optimised for 100 iterations to minimise the segmentation loss between the segmentation output and the DAE-cleaned output using a combination of Dice and L2 loss. This allows the input image contrast to be manipulated to minimise the difference between the predicted segmentation and the anatomical prior encoded in the DAE. This method relies on using the DAE to encode anatomical priors, and so it is not clear how it will perform given the heterogeneity of stroke lesions.
The next DA method to be used (referred to in results as ‘TENT’) is Test-time Entropy Minimisation (TENT) [37], where the objective is to maximise model confidence based on the entropy of its predictions. Although the original paper adapts by modifying the batch normalisation statistics, we instead opt to optimise a small normalisation network similar to the DAE workflow due to the limited batch size available when using large 3D volumes. The normalisation network is again re-initialised and optimised for 100 iterations for each test subject, using the Shannon entropy [38]:
\[\mathcal{H}_{\hat{y}} = - \Sigma p(\hat{y})\log p(\hat{y}),\]
where \(p(\hat{y})\) is the predicted segmentation probability.
The final method to be used is a form of pseudo-labelling (PL), where the entire test dataset is used to optimise all of the segmentation model’s parameters. Recent developments in this field focus on ways to clean the predicted pseudo-labels in order to restrict the new supervision to areas of high confidence [39]. To this end, three forms of PL are evaluated. The first PL method used (referred to in results as ‘PL’) simply thresholds the predicted probabilities at a relatively high probability (calculated as \(\frac{1.5}{N_{C}}\) where \(N_C\) is the total number of channels including background). In the second PL method (referred to in results as ‘UPL’), the thresholded predictions are further thresholded to include only regions of low uncertainty. Uncertainty is estimated using Monte Carlo dropout [40] with 10 iterations and thresholded at a value of 0.05 as specified in [39]. The final PL method (referred to in results as ‘DPL’) is a reproduction of [39] and introduces an additional masking based on class prototypes derived from feature maps in the segmentation model’s decoder. In all PL methods, a standard cross-entropy loss is used during optimisation with a class weighting based on the input pseudo-label and models are optimised for 2000 iterations. All DA methods (including DAE and TENT) are optimised using the AdamW optimiser [33] with a fixed learning rate of \(0.002\) and a weight decay of \(0.01\).
2.2 Pseudo labels↩︎
A unique benefit of the proposed Synth framework is its theoretical insensitivity to accuracy of lesion labels. In a standard supervised training framework, we need this label to be a perfect segmentation of the input image. In a synthetic framework, the input images are created \(from\) the ground truth labels and thus are intrinsically a perfect segmentation. As long as the predictions look like a plausible lesion, then imperfect ground truth labels should be of no detrimental effect in a synthetic framework.
Building on this logic, we explore the benefit of leveraging a large unlabelled dataset via pseudo-labelling. We use the baseline model trained on ATLAS, with TTA for robustness, to infer lesion labels for a private dataset of 1159 isotrophic MPRAGE images from the PLORAS study [41] containing chronic stroke.
3 Experiments↩︎
Models were validated on a number of datasets. We assessed the models’ in-domain performance on the hold-out test set for the ATLAS dataset (131 subjects, 1mm isotropic MPRAGE) for in-domain evaluation. For assessing OOD robustness, we use the ISLES 2015 dataset [42] (N=28 subjects, multi-modal MRI), the ARC dataset [43], [44] (N=229 subjects with T2 images, N=202 with T1, and N=85 with FLAIR) and a private dataset of N=263 subjects with combinations of T2 and FLAIR images resliced to 2mm isotropic and spatially normalised to the MNI template, referred to in this work as PLORAS [45]. The ISLES and PLORAS datasets also exhibit an additional domain shift due to the presence of acute pathology instead of chronic. This PLORAS dataset is distinct to the chronic MPRAGE cohort described in Section 2.2.
At test-time, images are loaded, oriented to RAS, resliced to 1 mm slice thickness, histogram normalised and images z-scored to a zero mean and unit standard deviation. Sliding-window inference was performed using a patch size of \(192\times192\times192\), using patches with a 50% overlap and a Gaussian weighting with \(\sigma=0.125\) when combining patches. Test-time augmentation was additionally performed (denoted in results as TTA) by averaging logits across all possible combinations of flips in the x, y and z axes. Predicted logits were then resliced to the original input image and a softmax applied to derive posterior probabilities. An argmax was then used to derive a binary lesion map. TTA is a popular heuristic method for increasing model robustness at test-time [35].
Multi-modal ensembling: In addition to per-modality evaluation, we provide results of ensembles of per-modality predictions to better represent how such a model may be used in practice. Logits were averaged first across all modalities before taking the softmax and post-processing as stated previously. Ensemble results are reported for ISLES 2015 and ARC datasets.
Comparison to the ground truth was performed by reslicing both the prediction and ground truth to 1 mm slice thickness and padding images to a size of \(256\times256\times256\). Segmentations were evaluated using the Dice coefficient and 95th-percentile Hausdorff distance (HD95). Further evaluation is reported in Appendix 6 using absolute volume difference (AVD), absolute lesion difference (ALD), and lesion-wise F1 score (LF1), true positive rate (TPR) and false positive rate (FPR).
The Dice coefficient measures overlap, where a score of 1 indicates perfect overlap and 0 indicates no overlap. The Hausdorff distance measures surface similarity by determining the shortest distance between surfaces at all given points, using the 95th-percentile value to avoid errors from anomalous values in imperfect masks. Note that a prediction of entirely background class will return the maximum side length of 256.
The absolute volume difference (given in units \(cm^3\)) gives a direct comparison of the overall proportion of brain labelled as unhealthy. The absolute lesion difference \(\mathcal{L}\) is the difference in the number of unique lesions, defined as \(\mathcal{L}(x, y) = \left| \mathcal{C}(x) - \mathcal{C}(y) \right|\), where \(\mathcal{C}\) is an algorithm used to calculate the number of connected components. Lastly, the lesion-wise F1 score uses the same equation as Dice but on a per-lesion basis rather than per-voxel: for each unique lesion in the ground-truth \(y\), if a single voxel of the predicted mask overlaps with the lesion then this is considered as a success. The Sensitivity score is a measure of the detection of true positives, given by \(\frac{TP}{TP+FN}\) where \(TP\) are true positives and \(FN\) are false negatives. The false-positive rate (FPR), the complement of specificity, is given by \(1-\frac{TN}{TN+FP}\) where \(TN\) are true negatives and \(FP\) are false positives.
Pseudo labels: We generate pseudo labels on the MPRAGE PLORAS dataset using the baseline model with TTA. Predictions are made on images normalised to the MNI template, meaning predictions are aligned to the healthy tissue maps. A new baseline model is then trained using the predicted image-label pairs combined with the original ATLAS training data. Likewise, a new Synth model is trained where labels are added to the set of label maps used for pasting, whilst the mixed healthy data is restricted to still only include the manually-labelled ATLAS dataset. These models are trained with the exact same settings as used for the original Synth and baseline models.
4 Results↩︎
Overall results are shown in Figure 3 for both models and their best-performing domain adaptation technique. Comparisons of all adaptation techniques can be seen in Tables 1, [tab:da-isles2015], 3 and 4.
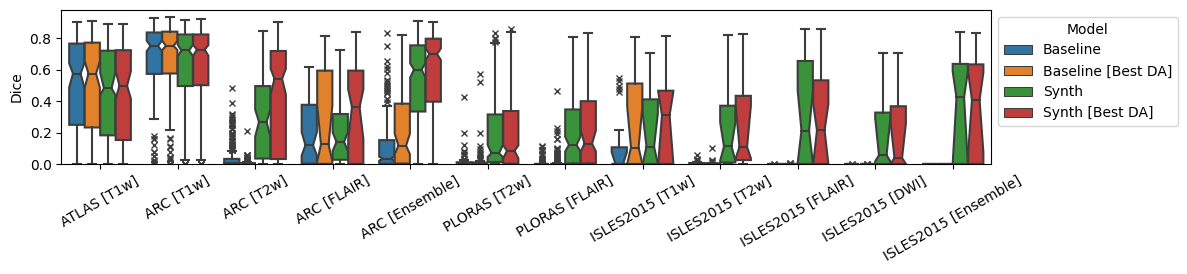
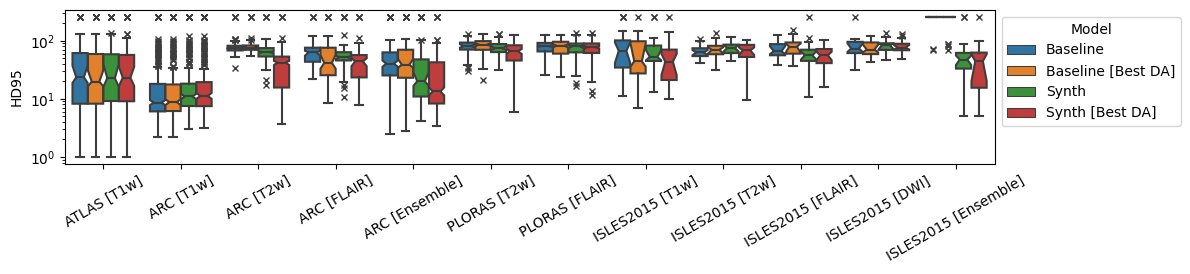
Figure 3: Dice and 95th-percentile Hausdorff Distance for all reported datasets. ‘Best DA’ indicates the best-performing domain adaptation technique for the model on the given dataset/modality..
4.1 ATLAS↩︎
In the ATLAS dataset, the task is considered completely in-domain so the Baseline model was expected to outperform the Synth model due to simulated data not containing all possible biomarkers from real images. As shown in Figure 3, the Baseline model performed as expected but the Synth model remained competitive, losing only in Dice and AVD. Table 1 shows that no differences between the two models are statistically significant. Table 11 shows that the Baseline model reported a greater mean TPR with and without TTA, at the expense of a higher FPR indicating a greater tendency to over-segment. The baseline having a better AVD and worse ALD, suggests that this over-segmentation may be due to mis-identifying lesions rather than over-extending the boundary of correctly identified lesions.
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.575 (0.523-0.627) | 23.5 (13.9-33.2) | |||||
| Baseline+TTA | 0.575 (0.522-0.628) | 19.7 (10.2-29.3) | ||||||
| Synth | 0.482 (0.431-0.534) | 22.6 (12.0-33.3) | ||||||
| Synth+TTA | 0.498 (0.446-0.550) | 23.0 (11.6-34.5) |
4.2 ISLES 2015↩︎
The ISLES 2015 dataset was the first benchmark used to evaluate behavior in OOD settings. The results in Figure 3 and Table [tab:da-isles2015] show that the Synth model outperforms the Baseline model in all modalities except T1w and DWI in regards to Dice with high statistical significance. It is worth noting that, in modalities where models performed relatively poorly, the FPR scores were higher without a large decrease in TPR (Table 12). This suggests that the poor performance in OOD may be attributable to false positives rather than false negatives. Both models scored lower on this dataset’s T1w data than for the in-domain ATLAS T1w data, possibly due to differences between sub-acute strokes in the dataset and the chronic stroke images used in training.
Table [tab:da-isles2015] also reports all results for DA methods using both the baseline and Synth models. For the baseline model, in all cases except the near-domain T1w modality the DA methods fail to recover any accuracy from the initial model. In the case of T1w, only the DAE method leads to an improvement in Dice score. For the Synth data, in all modalities there is always at least one DA technique that leads to an improvement in Dice and HD95, with statistically significant improvements over the baseline visible in T1w and Ensemble modalities. This provides evidence that the more robust Synth model may provide an ideal starting point for DA techniques.
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.000 (0.000-0.074) | 67.0 (39.7-94.2) | |||||
| Baseline+TTA | 0.000 (0.000-0.064) | 69.8 (30.0-109.7) | ||||||
| Baseline+TENT | 0.000 (0.000-0.004) | 256.0 (216.6-295.4) | ||||||
| Baseline+DAE | 0.105 (0.000-0.217) | 44.1 (22.1-66.2) | ||||||
| Baseline+PL | 0.006 (0.000-0.028) | 76.8 (70.5-83.2) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.110 (0.012-0.208) | 52.5 (29.9-75.0) | ||||||
| Synth+TTA | 0.088 (0.000-0.188) | 44.8 (11.1-78.4) | ||||||
| Synth+TENT | 0.000 (0.000-0.075) | 79.6 (49.0-110.2) | ||||||
| Synth+DAE | 0.311 (0.204-0.417) | 43.6 (22.9-64.2) | ||||||
| Synth+PL | 0.004 (0.000-0.040) | 51.0 (20.7-81.2) | ||||||
| Synth+UPL | 0.000 (0.000-0.000) | 256.0 (235.6-256.0) | ||||||
| Synth+DPL | 0.000 (0.000-0.001) | 256.0 (226.8-256.0) | ||||||
| T2w | Baseline | 0.000 (0.000-0.005) | 62.7 (56.3-69.1) | |||||
| Baseline+TTA | 0.000 (0.000-0.002) | 63.1 (57.8-68.4) | ||||||
| Baseline+TENT | 0.000 (0.000-0.001) | 85.7 (49.4-122.0) | ||||||
| Baseline+DAE | 0.000 (0.000-0.008) | 69.8 (61.3-78.3) | ||||||
| Baseline+PL | 0.000 (0.000-0.002) | 69.5 (62.8-76.2) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.111 (0.007-0.216) | 75.0 (68.4-81.7) | ||||||
| Synth+TTA | 0.102 (0.000-0.211) | 74.4 (68.0-80.8) | ||||||
| Synth+TENT | 0.105 (0.005-0.205) | 70.7 (61.5-79.9) | ||||||
| Synth+DAE | 0.108 (0.000-0.218) | 68.1 (58.0-78.1) | ||||||
| Synth+PL | 0.117 (0.004-0.230) | 74.1 (67.4-80.8) | ||||||
| Synth+UPL | 0.004 (0.000-0.098) | 63.7 (57.0-70.3) | ||||||
| Synth+DPL | 0.000 (0.000-0.076) | 62.2 (52.6-71.8) | ||||||
| FLAIR | Baseline | 0.000 (0.000-0.000) | 65.8 (56.9-74.7) | |||||
| Baseline+TTA | 0.000 (0.000-0.000) | 71.8 (38.5-105.2) | ||||||
| Baseline+TENT | 0.000 (0.000-0.000) | 92.4 (63.0-121.9) | ||||||
| Baseline+DAE | 0.000 (0.000-0.000) | 79.0 (68.5-89.5) | ||||||
| Baseline+PL | 0.000 (0.000-0.000) | 69.6 (54.5-84.7) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.212 (0.085-0.340) | 56.1 (38.7-73.4) | ||||||
| Synth+TTA | 0.226 (0.097-0.355) | 52.2 (19.1-85.3) | ||||||
| Synth+TENT | 0.000 (0.000-0.090) | 71.0 (58.6-83.5) | ||||||
| Synth+DAE | 0.214 (0.099-0.329) | 56.1 (47.3-64.9) | ||||||
| Synth+PL | 0.122 (0.004-0.240) | 76.1 (64.2-87.9) | ||||||
| Synth+UPL | 0.000 (0.000-0.117) | 71.6 (27.8-115.5) | ||||||
| Synth+DPL | 0.000 (0.000-0.111) | 170.8 (126.7-214.8) | ||||||
| DWI | Baseline | 0.000 (0.000-0.000) | 73.1 (57.5-88.7) | |||||
| Baseline+TTA | 0.000 (0.000-0.000) | 83.7 (57.3-110.2) | ||||||
| Baseline+TENT | 0.000 (0.000-0.000) | 84.3 (58.7-109.8) | ||||||
| Baseline+DAE | 0.000 (0.000-0.000) | 70.5 (62.1-78.9) | ||||||
| Baseline+PL | 0.000 (0.000-0.006) | 72.9 (65.1-80.8) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.056 (0.000-0.144) | 84.9 (77.2-92.6) | ||||||
| Synth+TTA | 0.051 (0.000-0.145) | 82.7 (75.2-90.2) | ||||||
| Synth+TENT | 0.000 (0.000-0.084) | 78.4 (65.3-91.6) | ||||||
| Synth+DAE | 0.039 (0.000-0.132) | 75.9 (68.4-83.5) | ||||||
| Synth+PL | 0.151 (0.068-0.234) | 80.9 (74.4-87.5) | ||||||
| Synth+UPL | 0.038 (0.000-0.137) | 71.5 (59.7-83.3) | ||||||
| Synth+DPL | 0.000 (0.000-0.069) | 69.0 (30.4-107.6) | ||||||
| Ensemble | Baseline | 0.000 (0.000-0.000) | 256.0 (237.2-256.0) | |||||
| Baseline+TTA | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+TENT | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DAE | 0.000 (0.000-0.000) | 256.0 (231.8-256.0) | ||||||
| Baseline+PL | 0.000 (0.000-0.000) | 256.0 (223.0-256.0) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.423 (0.302-0.545) | 47.3 (24.2-70.4) | ||||||
| Synth+TTA | 0.462 (0.338-0.586) | 43.1 (12.2-74.0) | ||||||
| Synth+TENT | 0.000 (0.000-0.099) | 66.9 (27.2-106.5) | ||||||
| Synth+DAE | 0.408 (0.288-0.528) | 44.6 (25.0-64.1) | ||||||
| Synth+PL | 0.081 (0.000-0.187) | 58.7 (50.0-67.4) | ||||||
| Synth+UPL | 0.000 (0.000-0.023) | 256.0 (224.0-256.0) | ||||||
| Synth+DPL | 0.000 (0.000-0.037) | 256.0 (216.4-256.0) |
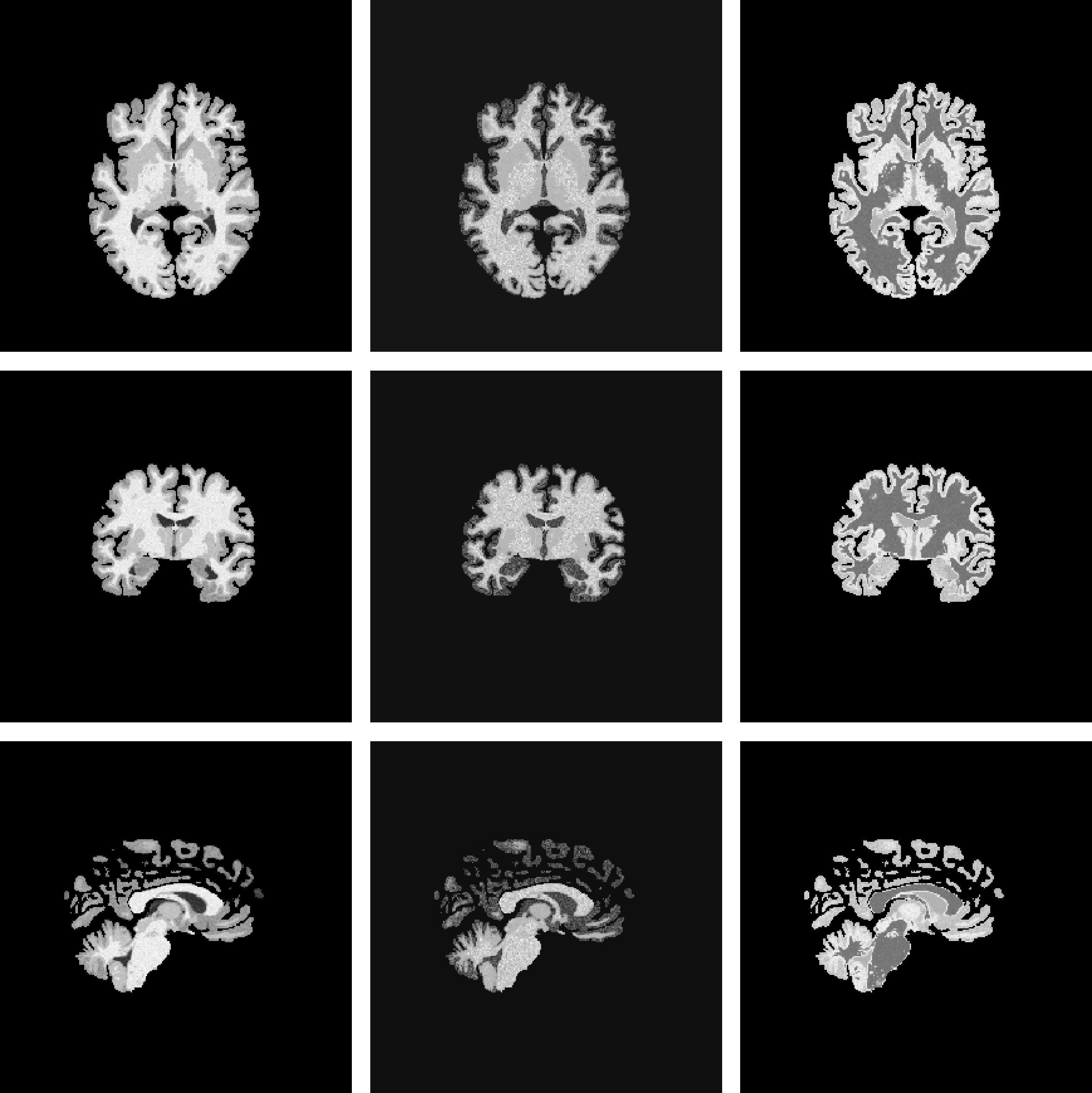
In an ensemble of the four modalities available per-subject, for all instances the Baseline model failed and gave an empty prediction leading to the zero Dice scores observed in Table [tab:da-isles2015]. In contrast, the Synth model’s ensembled prediction significantly outperformed any of the single modalities in Dice score. A visualisation of the ensembled predictions can be seen in Figure 4. It is also noted that ensembling is expected to reduce the likelihood of models mis-labelling irrelevant hyperintensity in sequences such as FLAIR and DWI.




Figure 4: Sample TTA predictions with ensembling method in the ISLES 2015 dataset. Color code in predicted Synth labels: dark-blue = Gray Matter, green = White Matter, light-blue = Gray/White Matter partial volume, amber = CSF, red = stroke..
4.3 ARC↩︎
The ARC dataset is a dataset of research-quality scans for chronic stroke patients, and should therefore represent a less dramatic domain shift. The T1w results in Table 3, which represent the closest domain to training, support this expectation with both the baseline and the Synth model achieving strong Dice and HD95 scores with no statistical significance between them. The results for the T2 modality and the overall ensemble support the Synth model’s performance in OOD scenarios, demonstrating a statistically significant improvement over the baseline. The T1w performance in both models is significantly higher in Dice than the Synth model’s ensemble result, however there is no significant difference in HD95. The ensemble scenario better reflects the likely use-case in a clinical setting, where data may be highly varied in the combinations of channels available at test-time. Strong performance on both the T1w data and the full ensemble could support a scenario where T1w data is used alone when available, and otherwise all other channels are combined in an ensemble.
Scores are also reported in Table 3 for all DA methods using both the baseline and Synth models. The baseline model still achieves the highest score in both Dice and HD95 for the near-domain T1w data, however there is no significant difference between the baseline and the Synth model for both metrics. For the Synth model, all modalities see benefit from a range of DA methods: for T1w, TTA leads to a slight increase in Dice while DAE leads to a slight improvement in HD95; for T2w, both DAE and PL lead to significant improvements over the standard Synth model in both Dice and HD95; for FLAIR, improvements in Dice are seen for PL, TENT and DAE with the greatest improvement from TENT (with statistical significance in Dice). For the ensemble of all individual modalities, improvements in Dice are observed for TTA and DAE with the greatest coming from DAE. This provides further evidence that the robust initial predictions of the Synth model enable optimisation with DA methods. Notably the pseudo-labelling methods have a much lower success rate. It is possible that, after improving initial predictions with one of the other DA methods, further improvements could be made by fine-tuning on DA-enhanced pseudo-labels. These methods may also require further tailoring to the relatively difficult task of brain lesion segmentation.
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.752 (0.715-0.790) | 8.6 (2.3-14.9) | |||||
| Baseline+TTA | 0.752 (0.713-0.790) | 8.8 (2.5-15.0) | ||||||
| Baseline+TENT | 0.000 (0.000-0.029) | 105.3 (91.5-119.1) | ||||||
| Baseline+DAE | 0.710 (0.674-0.746) | 12.1 (6.2-18.0) | ||||||
| Baseline+PL | 0.343 (0.311-0.375) | 64.9 (60.5-69.3) | ||||||
| Baseline+UPL | 0.339 (0.299-0.379) | 40.2 (28.8-51.6) | ||||||
| Baseline+DPL | 0.339 (0.301-0.377) | 24.2 (15.3-33.1) | ||||||
| Synth | 0.723 (0.684-0.762) | 11.0 (4.0-18.0) | ||||||
| Synth+TTA | 0.729 (0.690-0.768) | 11.2 (4.5-17.9) | ||||||
| Synth+TENT | 0.676 (0.638-0.715) | 13.6 (6.8-20.4) | ||||||
| Synth+DAE | 0.712 (0.676-0.747) | 10.5 (5.5-15.5) | ||||||
| Synth+PL | 0.296 (0.261-0.332) | 168.1 (162.1-174.0) | ||||||
| Synth+UPL | 0.368 (0.332-0.405) | 22.9 (14.2-31.6) | ||||||
| Synth+DPL | 0.234 (0.203-0.266) | 21.2 (10.1-32.3) | ||||||
| T2w | Baseline | 0.004 (0.000-0.014) | 74.2 (71.1-77.2) | |||||
| Baseline+TTA | 0.000 (0.000-0.007) | 74.4 (71.4-77.4) | ||||||
| Baseline+TENT | 0.000 (0.000-0.000) | 111.5 (100.4-122.5) | ||||||
| Baseline+DAE | 0.000 (0.000-0.016) | 77.1 (73.7-80.6) | ||||||
| Baseline+PL | 0.001 (0.000-0.004) | 76.1 (73.1-79.0) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.268 (0.233-0.302) | 64.0 (60.5-67.4) | ||||||
| Synth+TTA | 0.221 (0.186-0.257) | 64.9 (61.4-68.4) | ||||||
| Synth+TENT | 0.159 (0.115-0.203) | 54.1 (49.5-58.6) | ||||||
| Synth+DAE | 0.543 (0.501-0.585) | 42.0 (37.8-46.3) | ||||||
| Synth+PL | 0.427 (0.395-0.458) | 62.7 (59.5-65.8) | ||||||
| Synth+UPL | 0.069 (0.052-0.087) | 46.9 (43.5-50.3) | ||||||
| Synth+DPL | 0.016 (0.006-0.027) | 49.0 (45.6-52.4) | ||||||
| FLAIR | Baseline | 0.120 (0.076-0.163) | 63.0 (54.1-71.9) | |||||
| Baseline+TTA | 0.122 (0.076-0.169) | 58.5 (49.5-67.4) | ||||||
| Baseline+TENT | 0.000 (0.000-0.017) | 153.6 (134.5-172.7) | ||||||
| Baseline+DAE | 0.124 (0.058-0.190) | 41.5 (31.2-51.7) | ||||||
| Baseline+PL | 0.089 (0.064-0.115) | 77.0 (69.4-84.5) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.141 (0.097-0.185) | 52.2 (43.3-61.1) | ||||||
| Synth+TTA | 0.112 (0.068-0.155) | 48.8 (39.6-57.9) | ||||||
| Synth+TENT | 0.361 (0.296-0.426) | 44.3 (34.5-54.1) | ||||||
| Synth+DAE | 0.148 (0.087-0.209) | 46.5 (37.0-56.1) | ||||||
| Synth+PL | 0.277 (0.236-0.318) | 100.3 (91.9-108.7) | ||||||
| Synth+UPL | 0.000 (0.000-0.014) | 56.0 (36.5-75.5) | ||||||
| Synth+DPL | 0.000 (0.000-0.006) | 103.3 (81.6-125.0) | ||||||
| Ensemble | Baseline | 0.034 (0.013-0.054) | 40.4 (33.5-47.3) | |||||
| Baseline+TTA | 0.012 (0.000-0.032) | 48.5 (40.4-56.6) | ||||||
| Baseline+TENT | 0.000 (0.000-0.004) | 256.0 (248.6-256.0) | ||||||
| Baseline+DAE | 0.117 (0.086-0.147) | 38.7 (32.8-44.5) | ||||||
| Baseline+PL | 0.002 (0.000-0.007) | 72.8 (69.7-75.9) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.602 (0.566-0.638) | 20.1 (14.8-25.3) | ||||||
| Synth+TTA | 0.614 (0.578-0.650) | 18.6 (13.4-23.8) | ||||||
| Synth+TENT | 0.518 (0.474-0.561) | 18.1 (10.7-25.4) | ||||||
| Synth+DAE | 0.700 (0.663-0.738) | 13.4 (8.9-18.0) | ||||||
| Synth+PL | 0.609 (0.575-0.643) | 52.3 (47.7-57.0) | ||||||
| Synth+UPL | 0.212 (0.184-0.241) | 25.2 (15.9-34.5) | ||||||
| Synth+DPL | 0.109 (0.085-0.133) | 31.2 (19.9-42.4) |
4.4 PLORAS↩︎
This dataset is intended to be the most challenging dataset included in this work and the most representative of real clinical data, with large diversity in acquisition setting and in slice thickness. For both available modalities, the Synth model outperforms the baseline with statistical significance in Dice both with and without TTA.
Results are reported for the dataset in Figure 3 and Table 4. In the T2 modality, only the DAE method leads to improvement over the regular Synth model, albeit without statistical significance. For the FLAIR images, both TTA and UPL lead to a slight improvement in Dice over the standard Synth model, again without any statistical significance. The DAE method leads to a significant improvement in HD95 but a degradation in Dice. In both modalities, no method leads to a significant improvement for the baseline model.
A number of samples are also visualised for this dataset in Figure 5, including the result of each DA technique. The first, second and fourth row are all examples where the baseline Dice score is zero and the Synth model’s Dice score is over 0.6. In the third row, the baseline Dice is also zero but the Synth model Dice is also lower with a score of 0.2. In this instance, the model has correctly identified the lesion but has also mislabelled a large number of false positives in other locations. In the use-case of interactive segmentation, such an output could easily be refined with click-interactions to remove false-positive objects in existing medical imaging software. The sample images show that TTA is the most conservative of the DA techniques, whilst TENT/DAE provide a middle ground between this and the extreme changes observed under the various PL methods.
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T2 | Baseline | 0.000 (0.000-0.013) | 80.5 (75.7-85.3) | |||||
| Baseline+TTA | 0.000 (0.000-0.008) | 78.4 (73.8-83.1) | ||||||
| Baseline+TENT | 0.000 (0.000-0.001) | 80.2 (65.9-94.4) | ||||||
| Baseline+DAE | 0.000 (0.000-0.020) | 85.1 (79.9-90.3) | ||||||
| Baseline+PL | 0.000 (0.000-0.003) | 79.0 (74.4-83.6) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.068 (0.014-0.121) | 73.4 (68.5-78.3) | ||||||
| Synth+TTA | 0.070 (0.014-0.125) | 73.4 (68.0-78.8) | ||||||
| Synth+TENT | 0.029 (0.000-0.080) | 78.2 (73.0-83.5) | ||||||
| Synth+DAE | 0.084 (0.024-0.144) | 66.3 (60.1-72.5) | ||||||
| Synth+PL | 0.002 (0.000-0.031) | 60.8 (53.0-68.7) | ||||||
| Synth+UPL | 0.000 (0.000-0.009) | 144.5 (124.5-164.4) | ||||||
| Synth+DPL | 0.000 (0.000-0.020) | 75.9 (56.3-95.6) | ||||||
| FLAIR | Baseline | 0.000 (0.000-0.003) | 80.6 (78.0-83.2) | |||||
| Baseline+TTA | 0.000 (0.000-0.002) | 80.6 (77.5-83.8) | ||||||
| Baseline+TENT | 0.000 (0.000-0.002) | 82.2 (72.7-91.6) | ||||||
| Baseline+DAE | 0.000 (0.000-0.007) | 82.1 (79.1-85.2) | ||||||
| Baseline+PL | 0.000 (0.000-0.001) | 83.0 (80.7-85.3) | ||||||
| Baseline+UPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Baseline+DPL | 0.000 (0.000-0.000) | 256.0 (256.0-256.0) | ||||||
| Synth | 0.121 (0.088-0.154) | 79.9 (76.8-82.9) | ||||||
| Synth+TTA | 0.129 (0.095-0.164) | 77.6 (74.3-80.8) | ||||||
| Synth+TENT | 0.001 (0.000-0.034) | 78.8 (71.4-86.3) | ||||||
| Synth+DAE | 0.044 (0.007-0.080) | 71.6 (67.9-75.3) | ||||||
| Synth+PL | 0.103 (0.074-0.133) | 91.3 (88.4-94.2) | ||||||
| Synth+UPL | 0.152 (0.119-0.185) | 79.6 (76.1-83.2) | ||||||
| Synth+DPL | 0.000 (0.000-0.015) | 79.9 (68.2-91.5) |




Figure 5: Sample visualisations in the PLORAS dataset..
4.5 Ablation: To mix or not to mix?↩︎
For all experiments shown thus far, the Synth model used a mix of both synthetic data and the real ATLAS dataset. In order to evaluate whether this decision is justified, an ablation is performed where the Synth model using mixed real/synthetic data is compared to a model trained with only synthetic data. This model is trained in the exact same manner as described previously for the baseline and Synth models. Results for the test datasets ATLAS, ISLES 2015 and ARC are shown in Tables 5, 6 and 7 respectively. In the in-domain ATLAS T1w data, the Synth model without mixed real data performs significantly worse than both the mixed data Synth model and the baseline model. In the ISLES 2015 dataset, the model without real data performs significantly better in Dice for the T1w modality. For all other modalities, there is no significant difference between the two Synth models in Dice score. Finally, in the ISLES dataset the model without any real data again performs significantly worse than both others in the near-domain T1w images. It does however perform significantly better than both others for the T2 data.
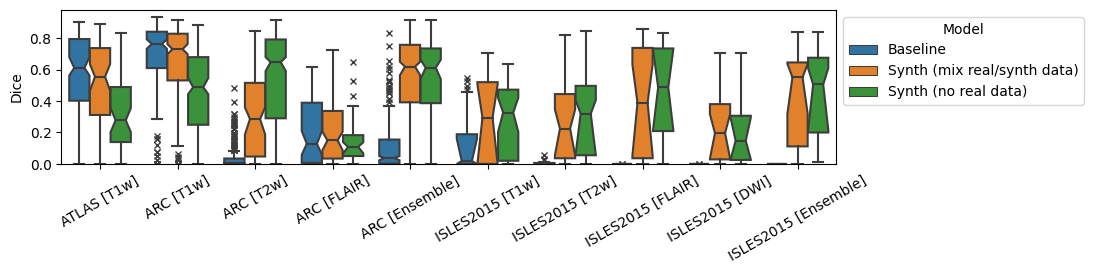
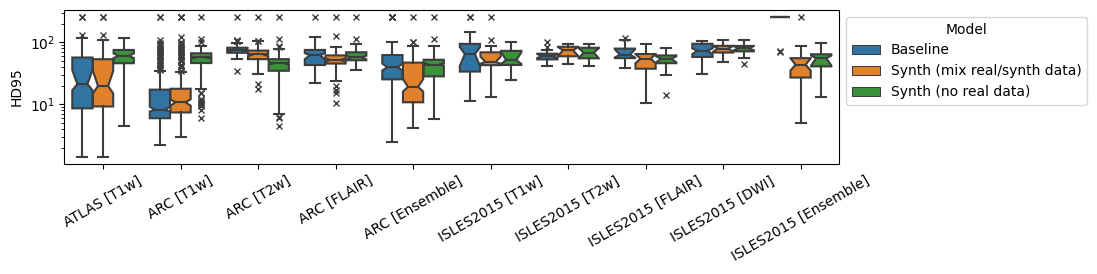
Figure 6: Dice and 95th-percentile Hausdorff Distance for all reported datasets, for models trained on different combinations of real/synthetic data..
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.575 (0.523-0.627) | 23.5 (13.9-33.2) | |||||
| Synth (no real data) | 0.197 (0.155-0.239) | 63.7 (59.6-67.9) | ||||||
| Synth (mix real/synth data) | 0.482 (0.431-0.534) | 22.6 (12.0-33.3) |
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.000 (0.000-0.074) | 67.0 (39.7-94.2) | |||||
| Synth (no real data) | 0.304 (0.213-0.396) | 58.6 (48.5-68.6) | ||||||
| Synth (mix real/synth data) | 0.110 (0.012-0.208) | 52.5 (29.9-75.0) | ||||||
| T2w | Baseline | 0.000 (0.000-0.005) | 62.7 (56.3-69.1) | |||||
| Synth (no real data) | 0.074 (0.000-0.184) | 72.3 (65.7-78.9) | ||||||
| Synth (mix real/synth data) | 0.111 (0.007-0.216) | 75.0 (68.4-81.7) | ||||||
| FLAIR | Baseline | 0.000 (0.000-0.000) | 65.8 (56.9-74.7) | |||||
| Synth (no real data) | 0.372 (0.255-0.489) | 56.1 (49.5-62.7) | ||||||
| Synth (mix real/synth data) | 0.212 (0.085-0.340) | 56.1 (38.7-73.4) | ||||||
| DWI | Baseline | 0.000 (0.000-0.000) | 73.1 (57.5-88.7) | |||||
| Synth (no real data) | 0.082 (0.000-0.168) | 83.7 (76.3-91.0) | ||||||
| Synth (mix real/synth data) | 0.056 (0.000-0.144) | 84.9 (77.2-92.6) | ||||||
| Ensemble | Baseline | 0.000 (0.000-0.000) | 256.0 (237.2-256.0) | |||||
| Synth (no real data) | 0.272 (0.157-0.388) | 60.1 (49.7-70.5) | ||||||
| Synth (mix real/synth data) | 0.423 (0.302-0.545) | 47.3 (24.2-70.4) |
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.752 (0.715-0.790) | 8.6 (2.3-14.9) | |||||
| Synth (no real data) | 0.467 (0.430-0.504) | 57.1 (52.9-61.3) | ||||||
| Synth (mix real/synth data) | 0.723 (0.684-0.762) | 11.0 (4.0-18.0) | ||||||
| T2w | Baseline | 0.004 (0.000-0.014) | 74.2 (71.1-77.2) | |||||
| Synth (no real data) | 0.626 (0.588-0.665) | 46.1 (42.2-50.0) | ||||||
| Synth (mix real/synth data) | 0.268 (0.233-0.302) | 64.0 (60.5-67.4) | ||||||
| FLAIR | Baseline | 0.120 (0.076-0.163) | 63.0 (54.1-71.9) | |||||
| Synth (no real data) | 0.096 (0.070-0.123) | 57.6 (49.2-65.9) | ||||||
| Synth (mix real/synth data) | 0.141 (0.097-0.185) | 52.2 (43.3-61.1) | ||||||
| Ensemble | Baseline | 0.034 (0.013-0.054) | 40.4 (33.5-47.3) | |||||
| Synth (no real data) | 0.597 (0.562-0.631) | 44.0 (39.9-48.2) | ||||||
| Synth (mix real/synth data) | 0.602 (0.566-0.638) | 20.1 (14.8-25.3) |
4.6 Use of Pseudo-labelling↩︎
The use of synthetic data for semi-supervised pseudo-label training is also explored through the use of a large collection of MPRAGE volumes from the PLORAS study [45]. Results in Figure 7 and Tables 8, 9 and 10 demonstrate an overall positive effect of pseudo labels in the Synth model, with the ARC ensemble result seeing a statistically significant increase in Dice as a result of the new data. The in-domain ATLAS dataset also shows a notable improvement for both models as a result of pseudo labels, with a more marked increase in the baseline model.
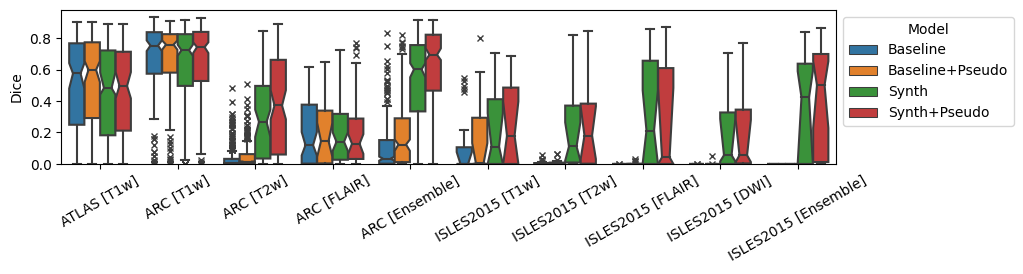
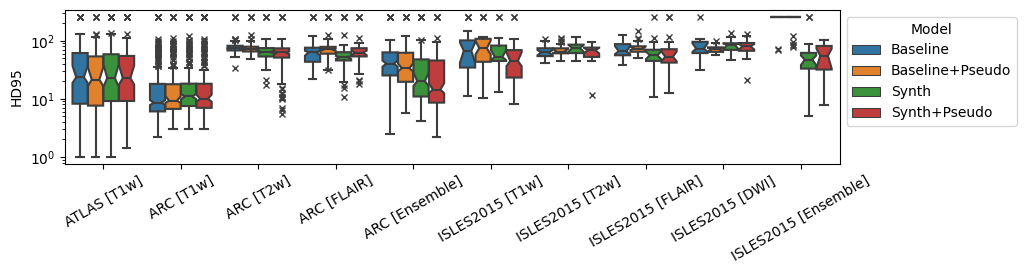
Figure 7: Dice and 95th-percentile Hausdorff Distance for all reported datasets, for models trained with/without an additional dataset of MPRAGE images and pseudo-labels..
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.575 (0.523-0.627) | 23.5 (13.9-33.2) | |||||
| Baseline+Pseudo | 0.598 (0.548-0.647) | 21.5 (13.8-29.1) | ||||||
| Synth | 0.482 (0.431-0.534) | 22.6 (12.0-33.3) | ||||||
| Synth+Pseudo | 0.496 (0.445-0.547) | 22.8 (11.5-34.1) |
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.000 (0.000-0.074) | 67.0 (39.7-94.2) | |||||
| Baseline+Pseudo | 0.003 (0.000-0.091) | 74.2 (48.3-100.0) | ||||||
| Synth | 0.110 (0.012-0.208) | 52.6 (30.0-75.1) | ||||||
| Synth+Pseudo | 0.179 (0.076-0.283) | 44.8 (20.9-68.8) | ||||||
| T2w | Baseline | 0.000 (0.000-0.005) | 62.7 (56.3-69.1) | |||||
| Baseline+Pseudo | 0.001 (0.000-0.007) | 64.9 (58.3-71.5) | ||||||
| Synth | 0.111 (0.007-0.216) | 75.0 (68.4-81.7) | ||||||
| Synth+Pseudo | 0.181 (0.071-0.291) | 68.3 (61.1-75.4) | ||||||
| FLAIR | Baseline | 0.000 (0.000-0.000) | 65.8 (56.9-74.7) | |||||
| Baseline+Pseudo | 0.000 (0.000-0.003) | 73.3 (65.4-81.3) | ||||||
| Synth | 0.212 (0.085-0.340) | 56.1 (38.7-73.4) | ||||||
| Synth+Pseudo | 0.042 (0.000-0.173) | 52.9 (30.4-75.4) | ||||||
| DWI | Baseline | 0.000 (0.000-0.000) | 73.1 (57.5-88.7) | |||||
| Baseline+Pseudo | 0.000 (0.000-0.004) | 71.6 (67.5-75.7) | ||||||
| Synth | 0.056 (0.000-0.144) | 84.9 (77.2-92.6) | ||||||
| Synth+Pseudo | 0.056 (0.000-0.147) | 80.4 (71.6-89.2) | ||||||
| Ensemble | Baseline | 0.000 (0.000-0.000) | 256.0 (237.2-256.0) | |||||
| Baseline+Pseudo | 0.000 (0.000-0.000) | 256.0 (231.1-256.0) | ||||||
| Synth | 0.423 (0.302-0.545) | 47.3 (24.2-70.4) | ||||||
| Synth+Pseudo | 0.501 (0.376-0.626) | 55.3 (43.7-67.0) |
| Modality | Model | Dice | HD95 | |||||
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.752 (0.715-0.790) | 8.6 (2.3-14.9) | |||||
| Baseline+Pseudo | 0.759 (0.721-0.797) | 9.3 (3.8-14.7) | ||||||
| Synth | 0.723 (0.684-0.762) | 11.0 (4.0-18.0) | ||||||
| Synth+Pseudo | 0.743 (0.704-0.782) | 10.0 (3.3-16.7) | ||||||
| T2w | Baseline | 0.004 (0.000-0.014) | 74.2 (71.1-77.2) | |||||
| Baseline+Pseudo | 0.014 (0.003-0.024) | 72.1 (69.0-75.1) | ||||||
| Synth | 0.268 (0.233-0.302) | 64.0 (60.5-67.4) | ||||||
| Synth+Pseudo | 0.372 (0.332-0.411) | 63.1 (59.2-66.9) | ||||||
| FLAIR | Baseline | 0.120 (0.076-0.163) | 63.0 (54.1-71.9) | |||||
| Baseline+Pseudo | 0.145 (0.101-0.189) | 70.6 (62.4-78.8) | ||||||
| Synth | 0.141 (0.097-0.185) | 52.2 (43.3-61.1) | ||||||
| Synth+Pseudo | 0.129 (0.084-0.173) | 62.1 (53.5-70.7) | ||||||
| Ensemble | Baseline | 0.034 (0.013-0.054) | 40.4 (33.5-47.3) | |||||
| Baseline+Pseudo | 0.124 (0.097-0.150) | 33.7 (28.8-38.6) | ||||||
| Synth | 0.602 (0.566-0.638) | 20.1 (14.8-25.3) | ||||||
| Synth+Pseudo | 0.694 (0.658-0.730) | 14.4 (9.9-18.9) |
5 Conclusion↩︎
In this study, we introduced a novel synthetic data generation and training framework for stroke lesion segmentation, building on the success of prior works in healthy brain parcellation. A model trained using this novel framework was evaluated on a wide range of datasets covering research and clinical data, and chronic and acute stroke pathologies. Results demonstrated that the proposed model is on par with the state-of-the-art for in-domain MPRAGE data, whilst being able to significantly outperform the state-of-the-art model in a variety of out-of-domain scenarios. This was further supported by comparison to a number of state-of-the-art domain adaptation techniques. These domain adaptation techniques consistently led to improvements from the base prediction of our new model, whilst degrading the already poor performance of the MPRAGE-trained model in all scenarios. This provides evidence for the value of our model as a robust ‘one size fits all’ base model that can provide an excellent initial prediction with which to adapt or fine-tune to a new domain.
Qualitative investigation also demonstrates the potential of the model for a starting checkpoint in an active-learning framework such as MONAI Label [46] where predictions may be refined to generate training data for task-specific fine-tuning. The uncertainty of healthy-tissue segmentations via MC dropout may also provide an effective heuristic for prioritising items to refine/label in such a framework [47].
Results also showed the potential benefit of the model for semi-supervised learning through pseudo labelling, where predicted labels may be fed back into the model with much less caution than is typically required when training with real images [48], [49]. A simple solution to further reinforce this may be to train a real/fake discriminator to perform automated quality-control and threshold optimisation for the generated binary maps.
Although results in the paper provide strong evidence of the raw value of the segmentation metrics, it is important to further validate that the predictions made from the trained model are useful for downstream tasks. This could be validated by comparing predictivity of the segmentation masks for functional scores such as the Comprehensive Aphasia Test (CAT) [50] or the NIH Stroke Score (NIHSS).
While this study focused on stroke, the results are expected to translate to other similar domains, such as haemorrhage and glioblastoma. Future work will compare the impact of the mixing proportions of real and synthetic data. Additionally, the utility of multi-modal data in a multi-channel model will be examined versus post-hoc averaging of individual modality predictions. Lesions often appear differently across modalities, so a model trained with multi-channel inputs is expected to leverage these differences more effectively. This relationship between multi-channel inputs may better be modelled using quantitative MRI data.
In the context of neuroimaging data, there are many shifts in domain beyond those related to scanner sequence and resolution targeted in this work. Shifts related to anatomical shape, brought on by changes in demographics or the presence of confounding conditions such as atrophy are of equal importance to shifts in image appearance. Prior work has attempted to model such factors through the use of causal inference and counterfactual generation [51]–[53]. It is conceivable that such an approach could be used to introduce morphological changes to the healthy tissue maps to create a model that is agnostic to shifts in domains related to both shape and appearance.
6 Further segmentation metrics↩︎
| Modality | Model | Dice | HD95 | AVD | ALD | LF1 | TPR | FPR |
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.500 | 44.3 | 7.60 | 3.48 | 0.480 | 0.510 | 0.251 |
| Baseline+TTA | 0.503 | 41.4 | 7.34 | 2.52 | 0.537 | 0.502 | 0.234 | |
| Synth | 0.456 | 47.4 | 8.73 | 2.26 | 0.536 | 0.426 | 0.200 | |
| Synth+TTA | 0.455 | 48.3 | 8.51 | 1.76 | 0.559 | 0.424 | 0.191 |
| Modality | Model | Dice | HD95 | AVD | ALD | LF1 | TPR | FPR |
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.115 | 84.2 | 38.14 | 3.32 | 0.269 | 0.076 | 0.034 |
| Baseline+TTA | 0.091 | 113.2 | 40.11 | 1.96 | 0.311 | 0.058 | 0.012 | |
| Baseline+TENT | 0.002 | 178.2 | 43.77 | 2.14 | 0.161 | 0.001 | 0.001 | |
| Baseline+DAE | 0.246 | 68.2 | 48.07 | 7.18 | 0.285 | 0.191 | 1.604 | |
| Baseline+PL | 0.040 | 81.6 | 42.79 | 643.29 | 0.003 | 0.039 | 1.979 | |
| Baseline+UPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Baseline+DPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Synth | 0.222 | 70.5 | 30.49 | 7.14 | 0.208 | 0.168 | 0.162 | |
| Synth+TTA | 0.230 | 78.5 | 31.41 | 2.18 | 0.349 | 0.163 | 0.085 | |
| Synth+TENT | 0.076 | 108.2 | 33.79 | 40.86 | 0.103 | 0.058 | 0.265 | |
| Synth+DAE | 0.268 | 58.1 | 29.18 | 3.64 | 0.316 | 0.223 | 0.293 | |
| Synth+PL | 0.050 | 76.9 | 42.55 | 3.93 | 0.321 | 0.028 | 0.008 | |
| Synth+UPL | 0.000 | 241.7 | 43.79 | 2.04 | 0.050 | 0.000 | 0.000 | |
| Synth+DPL | 0.001 | 221.7 | 43.77 | 2.46 | 0.127 | 0.000 | 0.000 | |
| T2w | Baseline | 0.007 | 65.4 | 50.81 | 15.00 | 0.078 | 0.044 | 2.786 |
| Baseline+TTA | 0.003 | 65.5 | 48.97 | 6.86 | 0.095 | 0.025 | 2.260 | |
| Baseline+TENT | 0.001 | 142.6 | 43.38 | 3.75 | 0.050 | 0.001 | 0.085 | |
| Baseline+DAE | 0.006 | 71.5 | 88.17 | 9.43 | 0.071 | 0.069 | 5.805 | |
| Baseline+PL | 0.002 | 74.2 | 71.28 | 155.21 | 0.013 | 0.005 | 5.055 | |
| Baseline+UPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Baseline+DPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Synth | 0.231 | 74.8 | 52.73 | 11.82 | 0.166 | 0.443 | 3.534 | |
| Synth+TTA | 0.245 | 74.6 | 50.99 | 4.68 | 0.279 | 0.454 | 3.379 | |
| Synth+TENT | 0.215 | 77.4 | 33.44 | 20.11 | 0.109 | 0.276 | 1.755 | |
| Synth+DAE | 0.255 | 63.1 | 31.10 | 4.61 | 0.280 | 0.328 | 1.437 | |
| Synth+PL | 0.245 | 73.3 | 37.57 | 13.71 | 0.161 | 0.288 | 2.280 | |
| Synth+UPL | 0.152 | 63.3 | 31.06 | 12.43 | 0.138 | 0.116 | 0.631 | |
| Synth+DPL | 0.111 | 58.6 | 35.25 | 8.11 | 0.172 | 0.073 | 0.143 | |
| FLAIR | Baseline | 0.000 | 71.4 | 40.06 | 10.79 | 0.018 | 0.000 | 0.515 |
| Baseline+TTA | 0.000 | 112.9 | 41.24 | 3.43 | 0.000 | 0.000 | 0.238 | |
| Baseline+TENT | 0.000 | 119.0 | 43.47 | 4.32 | 0.000 | 0.000 | 0.021 | |
| Baseline+DAE | 0.000 | 80.1 | 61.65 | 15.29 | 0.015 | 0.004 | 3.679 | |
| Baseline+PL | 0.000 | 77.1 | 43.43 | 70.43 | 0.009 | 0.000 | 0.490 | |
| Baseline+UPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Baseline+DPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Synth | 0.314 | 62.9 | 18.84 | 10.61 | 0.154 | 0.346 | 0.975 | |
| Synth+TTA | 0.329 | 82.1 | 18.37 | 3.50 | 0.275 | 0.359 | 0.891 | |
| Synth+TENT | 0.127 | 79.0 | 28.03 | 34.54 | 0.031 | 0.107 | 0.460 | |
| Synth+DAE | 0.274 | 55.7 | 20.25 | 7.86 | 0.152 | 0.305 | 0.989 | |
| Synth+PL | 0.252 | 75.7 | 50.59 | 111.43 | 0.036 | 0.330 | 3.176 | |
| Synth+UPL | 0.232 | 137.9 | 24.88 | 3.04 | 0.271 | 0.187 | 0.111 | |
| Synth+DPL | 0.205 | 145.6 | 25.16 | 7.36 | 0.236 | 0.168 | 0.191 | |
| DWI | Baseline | 0.000 | 80.1 | 42.63 | 5.54 | 0.023 | 0.000 | 0.138 |
| Baseline+TTA | 0.000 | 102.8 | 43.83 | 2.43 | 0.000 | 0.000 | 0.133 | |
| Baseline+TENT | 0.000 | 103.9 | 43.52 | 1.89 | 0.000 | 0.000 | 0.021 | |
| Baseline+DAE | 0.000 | 76.2 | 40.04 | 11.21 | 0.025 | 0.000 | 2.123 | |
| Baseline+PL | 0.004 | 77.5 | 40.33 | 835.36 | 0.001 | 0.004 | 0.726 | |
| Baseline+UPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Baseline+DPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Synth | 0.193 | 82.5 | 47.64 | 16.71 | 0.100 | 0.352 | 2.741 | |
| Synth+TTA | 0.204 | 81.1 | 44.32 | 8.39 | 0.187 | 0.336 | 2.344 | |
| Synth+TENT | 0.104 | 86.6 | 30.71 | 38.50 | 0.051 | 0.108 | 0.882 | |
| Synth+DAE | 0.185 | 80.4 | 39.10 | 12.36 | 0.106 | 0.262 | 2.139 | |
| Synth+PL | 0.186 | 85.2 | 81.64 | 17.43 | 0.120 | 0.397 | 5.759 | |
| Synth+UPL | 0.179 | 60.8 | 32.42 | 19.43 | 0.154 | 0.155 | 0.268 | |
| Synth+DPL | 0.089 | 117.4 | 39.27 | 3.75 | 0.300 | 0.060 | 0.031 | |
| Ensemble | Baseline | 0.000 | 242.8 | 43.79 | 2.00 | 0.000 | 0.000 | 0.000 |
| Baseline+TTA | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Baseline+TENT | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Baseline+DAE | 0.000 | 231.0 | 43.68 | 2.00 | 0.000 | 0.000 | 0.007 | |
| Baseline+PL | 0.000 | 198.9 | 43.79 | 2.11 | 0.024 | 0.000 | 0.000 | |
| Baseline+UPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Baseline+DPL | 0.000 | 256.0 | 43.79 | 2.11 | 0.000 | 0.000 | 0.000 | |
| Synth | 0.370 | 60.4 | 19.68 | 7.50 | 0.234 | 0.339 | 0.256 | |
| Synth+TTA | 0.378 | 69.7 | 20.01 | 2.75 | 0.348 | 0.334 | 0.223 | |
| Synth+TENT | 0.111 | 114.8 | 32.23 | 3.21 | 0.235 | 0.089 | 0.047 | |
| Synth+DAE | 0.365 | 51.4 | 19.84 | 3.75 | 0.354 | 0.331 | 0.204 | |
| Synth+PL | 0.246 | 60.7 | 29.01 | 21.18 | 0.125 | 0.188 | 0.150 | |
| Synth+UPL | 0.016 | 218.2 | 42.52 | 5.18 | 0.131 | 0.009 | 0.000 | |
| Synth+DPL | 0.033 | 187.3 | 41.09 | 6.04 | 0.223 | 0.020 | 0.000 |
| Modality | Model | Dice | HD95 | AVD | ALD | LF1 | TPR | FPR |
|---|---|---|---|---|---|---|---|---|
| T1w | Baseline | 0.646 | 24.5 | 18.04 | 6.19 | 0.335 | 0.600 | 1.178 |
| Baseline+TTA | 0.648 | 23.7 | 18.33 | 3.42 | 0.442 | 0.598 | 1.126 | |
| Baseline+TENT | 0.077 | 144.9 | 75.50 | 3.51 | 0.180 | 0.060 | 0.285 | |
| Baseline+DAE | 0.614 | 26.2 | 26.53 | 3.15 | 0.507 | 0.685 | 2.238 | |
| Baseline+PL | 0.325 | 67.5 | 146.72 | 175.61 | 0.017 | 0.613 | 10.342 | |
| Baseline+UPL | 0.341 | 74.4 | 48.10 | 22.84 | 0.244 | 0.262 | 0.695 | |
| Baseline+DPL | 0.340 | 52.5 | 52.48 | 9.53 | 0.324 | 0.247 | 0.465 | |
| Synth | 0.609 | 27.9 | 22.88 | 1.99 | 0.613 | 0.539 | 0.953 | |
| Synth+TTA | 0.611 | 27.0 | 24.08 | 1.84 | 0.640 | 0.534 | 0.885 | |
| Synth+TENT | 0.560 | 33.4 | 26.71 | 2.42 | 0.528 | 0.604 | 2.385 | |
| Synth+DAE | 0.613 | 23.4 | 20.60 | 2.26 | 0.581 | 0.640 | 1.903 | |
| Synth+PL | 0.311 | 158.6 | 48.41 | 260.54 | 0.017 | 0.310 | 2.303 | |
| Synth+UPL | 0.340 | 56.3 | 54.57 | 20.35 | 0.334 | 0.243 | 0.457 | |
| Synth+DPL | 0.255 | 58.3 | 63.36 | 7.44 | 0.530 | 0.169 | 0.339 | |
| T2w | Baseline | 0.040 | 76.8 | 73.80 | 47.12 | 0.044 | 0.063 | 6.778 |
| Baseline+TTA | 0.023 | 77.0 | 71.83 | 26.00 | 0.054 | 0.036 | 6.819 | |
| Baseline+TENT | 0.000 | 148.5 | 85.40 | 5.11 | 0.047 | 0.000 | 0.206 | |
| Baseline+DAE | 0.056 | 75.8 | 123.49 | 10.09 | 0.113 | 0.134 | 10.938 | |
| Baseline+PL | 0.006 | 78.8 | 127.78 | 353.31 | 0.007 | 0.014 | 12.731 | |
| Baseline+UPL | 0.000 | 256.0 | 85.74 | 2.57 | 0.013 | 0.000 | 0.185 | |
| Baseline+DPL | 0.000 | 256.0 | 85.74 | 2.57 | 0.013 | 0.000 | 0.185 | |
| Synth | 0.299 | 66.2 | 40.79 | 38.81 | 0.060 | 0.304 | 2.282 | |
| Synth+TTA | 0.284 | 66.2 | 43.70 | 16.00 | 0.117 | 0.274 | 1.893 | |
| Synth+TENT | 0.321 | 55.5 | 43.43 | 15.09 | 0.140 | 0.326 | 1.663 | |
| Synth+DAE | 0.437 | 40.8 | 40.19 | 11.43 | 0.196 | 0.410 | 1.344 | |
| Synth+PL | 0.384 | 65.5 | 40.26 | 22.77 | 0.095 | 0.475 | 3.881 | |
| Synth+UPL | 0.120 | 50.7 | 73.30 | 22.71 | 0.172 | 0.074 | 0.484 | |
| Synth+DPL | 0.055 | 52.3 | 78.43 | 47.28 | 0.108 | 0.032 | 0.447 | |
| FLAIR | Baseline | 0.193 | 66.2 | 52.15 | 49.49 | 0.049 | 0.205 | 4.532 |
| Baseline+TTA | 0.202 | 65.7 | 47.98 | 25.98 | 0.090 | 0.197 | 3.719 | |
| Baseline+TENT | 0.011 | 165.6 | 79.40 | 4.94 | 0.070 | 0.008 | 0.628 | |
| Baseline+DAE | 0.287 | 54.8 | 75.47 | 11.09 | 0.232 | 0.327 | 5.981 | |
| Baseline+PL | 0.126 | 81.9 | 162.13 | 382.66 | 0.007 | 0.240 | 13.548 | |
| Baseline+UPL | 0.000 | 256.0 | 82.36 | 2.62 | 0.035 | 0.000 | 0.497 | |
| Baseline+DPL | 0.000 | 256.0 | 82.36 | 2.62 | 0.035 | 0.000 | 0.497 | |
| Synth | 0.199 | 59.3 | 60.36 | 17.69 | 0.150 | 0.157 | 1.349 | |
| Synth+TTA | 0.190 | 56.4 | 62.98 | 8.36 | 0.256 | 0.143 | 1.185 | |
| Synth+TENT | 0.340 | 49.7 | 46.05 | 5.01 | 0.247 | 0.286 | 1.582 | |
| Synth+DAE | 0.263 | 51.5 | 53.14 | 5.88 | 0.248 | 0.215 | 1.581 | |
| Synth+PL | 0.276 | 96.8 | 45.97 | 93.18 | 0.027 | 0.255 | 2.133 | |
| Synth+UPL | 0.029 | 99.1 | 80.44 | 4.79 | 0.272 | 0.016 | 0.520 | |
| Synth+DPL | 0.010 | 146.9 | 81.38 | 7.11 | 0.189 | 0.005 | 0.512 | |
| Ensemble | Baseline | 0.107 | 53.3 | 77.04 | 22.20 | 0.309 | 0.071 | 1.137 |
| Baseline+TTA | 0.087 | 65.8 | 78.91 | 9.10 | 0.429 | 0.057 | 1.126 | |
| Baseline+TENT | 0.003 | 238.0 | 85.73 | 2.60 | 0.054 | 0.002 | 0.185 | |
| Baseline+DAE | 0.212 | 51.3 | 73.84 | 39.25 | 0.168 | 0.212 | 2.350 | |
| Baseline+PL | 0.016 | 76.1 | 70.76 | 512.92 | 0.004 | 0.014 | 3.869 | |
| Baseline+UPL | 0.000 | 256.0 | 85.74 | 2.57 | 0.013 | 0.000 | 0.185 | |
| Baseline+DPL | 0.000 | 256.0 | 85.74 | 2.57 | 0.013 | 0.000 | 0.185 | |
| Synth | 0.525 | 34.9 | 35.60 | 10.09 | 0.356 | 0.451 | 0.770 | |
| Synth+TTA | 0.530 | 33.0 | 36.51 | 4.50 | 0.470 | 0.452 | 0.696 | |
| Synth+TENT | 0.451 | 39.1 | 38.50 | 11.12 | 0.370 | 0.412 | 0.960 | |
| Synth+DAE | 0.579 | 27.6 | 27.52 | 6.77 | 0.432 | 0.531 | 0.923 | |
| Synth+PL | 0.529 | 50.2 | 33.21 | 29.02 | 0.106 | 0.515 | 1.551 | |
| Synth+UPL | 0.244 | 53.0 | 65.77 | 9.80 | 0.470 | 0.159 | 0.310 | |
| Synth+DPL | 0.172 | 71.4 | 71.62 | 13.97 | 0.414 | 0.107 | 0.284 |
| Modality | Model | Dice | HD95 | AVD | ALD | LF1 | TPR | FPR |
|---|---|---|---|---|---|---|---|---|
| T2 | Baseline | 0.017 | 79.8 | 116.97 | 11.99 | 0.108 | 0.046 | 8.483 |
| Baseline+TTA | 0.011 | 78.8 | 94.22 | 11.14 | 0.101 | 0.034 | 7.071 | |
| Baseline+TENT | 0.001 | 98.7 | 21.88 | 5.20 | 0.019 | 0.006 | 0.478 | |
| Baseline+DAE | 0.026 | 83.6 | 206.65 | 3.28 | 0.269 | 0.097 | 13.761 | |
| Baseline+PL | 0.004 | 76.8 | 51.10 | 19.19 | 0.032 | 0.009 | 3.874 | |
| Baseline+UPL | 0.000 | 256.0 | 22.47 | 3.29 | 0.000 | 0.005 | 0.414 | |
| Baseline+DPL | 0.000 | 256.0 | 22.47 | 3.29 | 0.000 | 0.005 | 0.414 | |
| Synth | 0.188 | 74.5 | 43.14 | 11.42 | 0.227 | 0.323 | 3.083 | |
| Synth+TTA | 0.195 | 72.3 | 38.65 | 6.56 | 0.310 | 0.314 | 2.771 | |
| Synth+TENT | 0.153 | 74.7 | 70.50 | 19.57 | 0.119 | 0.265 | 4.774 | |
| Synth+DAE | 0.208 | 63.3 | 29.07 | 5.42 | 0.280 | 0.275 | 2.008 | |
| Synth+PL | 0.077 | 65.3 | 23.96 | 3.78 | 0.232 | 0.079 | 1.300 | |
| Synth+UPL | 0.014 | 168.9 | 21.76 | 2.75 | 0.124 | 0.012 | 0.420 | |
| Synth+DPL | 0.027 | 110.9 | 20.14 | 2.94 | 0.097 | 0.021 | 0.489 | |
| FLAIR | Baseline | 0.005 | 77.9 | 37.54 | 19.76 | 0.028 | 0.010 | 2.930 |
| Baseline+TTA | 0.002 | 78.1 | 30.08 | 12.72 | 0.020 | 0.006 | 2.169 | |
| Baseline+TENT | 0.002 | 105.1 | 21.69 | 5.15 | 0.010 | 0.003 | 0.647 | |
| Baseline+DAE | 0.014 | 78.6 | 103.77 | 4.12 | 0.145 | 0.043 | 7.639 | |
| Baseline+PL | 0.003 | 81.7 | 102.92 | 118.06 | 0.015 | 0.011 | 7.674 | |
| Baseline+UPL | 0.000 | 256.0 | 22.72 | 3.05 | 0.000 | 0.002 | 0.537 | |
| Baseline+DPL | 0.000 | 256.0 | 22.72 | 3.05 | 0.000 | 0.002 | 0.537 | |
| Synth | 0.213 | 75.8 | 48.25 | 17.65 | 0.131 | 0.350 | 3.374 | |
| Synth+TTA | 0.228 | 74.7 | 40.69 | 8.99 | 0.189 | 0.341 | 2.874 | |
| Synth+TENT | 0.149 | 85.8 | 44.09 | 9.20 | 0.111 | 0.197 | 3.080 | |
| Synth+DAE | 0.210 | 68.7 | 41.66 | 8.85 | 0.170 | 0.268 | 3.082 | |
| Synth+PL | 0.190 | 90.7 | 92.65 | 23.32 | 0.131 | 0.437 | 6.027 | |
| Synth+UPL | 0.223 | 77.3 | 21.27 | 6.00 | 0.231 | 0.253 | 1.747 | |
| Synth+DPL | 0.048 | 111.4 | 21.41 | 3.05 | 0.207 | 0.031 | 0.584 |