Imitation Game: A Model-based and Imitation Learning Deep Reinforcement Learning Hybrid
April 02, 2024
Abstract
Autonomous and learning systems based on DRL have firmly established themselves as a foundation for approaches to creating resilient and efficient . However, most current approaches suffer from two distinct problems: Modern model-free algorithms such as SAC need a high number of samples to learn a meaningful policy, as well as a fallback to ward against concept drifts (e. g., catastrophic forgetting). In this paper, we present the work in progress towards a hybrid agent architecture that combines model-based DRL with imitation learning to overcome both problems.
1 Introduction↩︎
Efficient operation of CNI is a global, immediate need. The report of the IPCC of the UN indicates that greenhouse gas emissions must be halved by 2023 in order to constrain global warming to 1.5 °C. Approaches based on ML, agent systems, and learning agents — i. e., such based on DRL — have firmly established themselves in providing numerous aspects of efficiency increase as well as resilient operation. From the hallmark paper that introduced DRL [1] to the development of MuZero [2] and AlphaStar [3], learning agents research has inspired many applications in the energy domain, including real power management [4], reactive power management and voltage control [5], [6], black start [7], anomaly detection [8], or analysis of potential attack vectors [9], [10].
A promising, and also the simplest form to employ DRL-based agents is to make use of model-free algorithms, such as PPO, TD3, or SAC. Recent works show applications in, e. g., voltage control, real power management in order to increase the share of DERs, or frequency regulation [11].
However, model-free DRL approaches suffer from prominent problems that hinder their wide-scale rollout in power grids: low sample efficiency and the potential for catastrophic forgetting.
The first problem describes the way agents are trained. In DRL, the agent learns from interactions with its environment, receiving an indication of the success of its actions through the reward signal that serves as the agent’s utility function. Although modern model-free DRL algorithms show that they not only learn successful strategies but can also react very well to situations they did not encounter during training, they require several thousand steps to learn such a policy. As DRL agents need interaction with their environment (a simulated power grid in our case), making the training of DRL agents computationally expensive. Thus, the efficiency of one sample, i. e., the quadruplet of state, action taken in the state, reward received, and follow-up state, \((s, a, r, s')\), is low.
The second problem, catastrophic forgetting, describes that agents can act suboptimal, erroneous even, or seem to “forget” established and well-working strategies when introduced to a change in marginal distributions [12], [13]. The dominant literature concentrates on robotics and disjoint task sets; most approaches cater to this specific notion of specific tasks. However, in the power grid domain, there is no disjoint task set; instead, changes occur in the environment, which can start catastrophic forgetting in a subtle way.
A particular way to address the first problem is the notion of model-based DRL. Here, the agent incorporates a model of the world, which helps to not only gauge the effectiveness of an action but can also be queried internally to learn from [14]. Potential models for such an approach can also be surrogate models [15]. However, there currently is no architecture that also addresses the problem of catastrophic forgetting. Therefore, a clear research gap exists in constructing a DRL agent approach that can make use of current advances (i. e., specifically, train in an efficient manner), but is still reliable for usage in power grids. Although it has been noted that a combination of model-free DRL and a controller would provide important benefits [16], a recent survey notes that currently, only very limited work exists in this regard [11]; current approaches require a tight integration of the existing controller logic with the DRL algorithm [17]. Aiding the agent’s learning by also adding imitation learning is currently not done. However, current research seems to indicate that this is, in fact, necessary, and that agents able to cope with various distributional shifts must have learned a causal model of the data generator [18].
In this paper, we present such an agent approach. We describe the work in progress towards a hybrid agent architecture that makes use of a world model and can also efficiently learn from an existing policy, so-called imitation learning. Moreover, we use the existing, potentially non-optimal control strategy as a safety fallback to guarantee a certain behavior. We introduce the notion of a discriminator that is able to gauge between applying the DRL policy and the fallback policy. We showcase our approach with a case study in a voltage control setting.
The rest of this paper is structured as follows: In 2, we give a survey of the relevant related work. We introduce our hybrid agent and discriminator architecture in 3. We then describe our case study and obtained results in 4. We follow with a discussion of the results and implications in 5. We conclude in 6 and give an outlook towards future results and development of this work in progress.
2 Related Work↩︎
2.1 Deep Reinforcement Learning↩︎
DRL is based on the MDP, which is a quintuplet \((S, A, T, R, \gamma)\): \(S\) denotes the set of states (e. g., voltage magnitudes: \(S_t = \left\{ V_1(t), V_2(t), \dotsc, V_n(t) \right\}\)); \(A\) is the set of actions (e. g., the reactive power generation or consumption of a node the agent controls: \(A_t = \left\{ q_1(t), q_2(t), \dotsc, q_n(t) \right\}\)); \(T\) are the conditional transition probabilities between any two states; \(R\) is the reward function of the agent \(R: S \times A \rightarrow \mathbb{R}\); and \(\gamma\), the discount factor, which is a hyperparameter designating how much future rewards will be considered in calculating the absolute Gain of an episode.
Essentially, an agent observes a state \(s_t\) at the time \(t\), performs an action \(a_t\), and receives a reward \(r_t\). Transition to the following state \(s_{t+1}\) can be deterministic or probabilistic, depending on \(T\). The Markov property states that for each state \(s_t\) with an action \(a_t\), only the previous state \(s_{t-1}\) is relevant for the evaluation of the transition. To capture a multi-level context and maintain the Markov property, \(s_t\) is usually enriched with information from previous states or the relevant context.
The goal of reinforcement learning is generally to learn a policy in which \(a_t \sim \pi_\theta(\cdot | s_t)\). The search for the optimal policy \(\pi_\theta^*\) is the optimization problem on which all reinforcement learning algorithms are based.
[1] proposed DRL with their DQNs. The reinforcement learning itself precedes this publication [19]. However, Mnih et al. were able to introduce deep neural networks as estimators for Q-values that enable robust training. Their end-to-end learning approach is still one of the standard benchmarks in DRL. The DQN approach has seen extensions until the Rainbow DQN [20] and newer work covers DQN approaches connected to behavior cloning [21]. Through, DQN only applies to environments with discrete actions.
DDPG [22] also builds on the policy gradient methodology: It concurrently learns a Q-function and policy. It is an off-policy algorithm that uses the Q-function estimator to train the policy. DDPG allows for continuous control; it can be seen as DQN for continuous action spaces. DDPG suffers from overestimating Q-values over time; TD3 has been introduced to fix this behavior [23].
PPO [24] is an on-policy policy gradient algorithm that can be used for discrete and continuous action spaces. It is a development parallel to DDPG and TD3, not an immediate successor. PPO is more robust towards hyperparameter settings than DDPG and TD3 are. Still, as an on-policy algorithm, it requires more interaction with the environment train, making it unsuitable for computationally expensive simulations.
SAC, having been published close to concurrently with TD3, targets the exploration-exploitation dilemma by being based on entropy regularization [25]. It is an off-policy algorithm originally focused on continuous action spaces but has been extended to support discrete action spaces as well. There also are approaches for distributed SAC [26].
PPO, TD3, and SAC are the most commonly used model-free DRL algorithms today. Of these, off-policy learning algorithms are naturally suited for behavior cloning and imitation learning, as on-policy algorithms, by their nature, need data generated by the current policy to train.
Learning from existing data without interaction with an environment is called offline reinforcement learning [27]. This approach can be employed to learn from existing experiences. The core of reinforcement learning is the interaction with the environment. Only when the agent explores the environment, creating trajectories and receiving rewards, can it optimize its policy. However, more realistic environments, like robotics or the simulation of large power grids, are computationally expensive. Training from already existing data would be beneficial. For example, an agent could learn from an existing simulation run for optimal voltage control before being trained to tackle more complex scenarios.
The field of offline reinforcement learning can roughly be subdivided into policy constraints, importance sampling, regularization, model-based offline reinforcement learning, one-step learning, imitation learning, and trajectory optimization. [[28]]1 and [27] have published extensive tutorial and review papers, to which we refer the interested reader instead of providing a poor replication of their work here. Instead, we will give only a concise overview considering the ones relevant for this work.
Of the mentioned methods, imitation learning is especially of interest. It means the agent can observe the actions of another agent (e.g., an existing controller) and learn to imitate it. Imitation learning aims to reduce the distance between the policy out of the dataset \(D\) and the agent’s policy, such that the optimization goal is expressed by \(J(\theta) = D(\pi_\beta(\cdot | \boldsymbol{s}), \pi_\theta(\cdot | \boldsymbol{s}))\). This so-called Behavior Cloning requires an expert behavior policy, which can be hard to come by but is readily available in some power-grid-related use cases, such as voltage control, where a simple voltage controller could be queried as the expert.
2.2 Model-free and Model-based Deep Reinforcement Learning for Power Grids↩︎
As of today, a large corpus of works exists that consider the application of DRL to power grid topics. As we have to constrain ourselves to works relevant to this paper, we refer the interested reader to current survey papers, such as the one created by [11] for model-free and [29] for model-based learning, for a more complete overview.
One of the dominant topics for applying DRL in power grids is voltage and reactive power control. As voltage control tasks dominate distribution systems, steady-state simulations can be employed, making the connection to DRL frameworks comparatively easy and helping maintain the Markov property. Also, the design of the reward function is easy, allowing a concise notation such as \(R = -\sum_i (V_i - 1)\).
To capture the underlying physical properties of the power grid better, [30] utilize GCNNs. Other recent publications employ DDPG for reactive power control, adding stability guarantees to the actor-network or training [31], [32]. Model-based approaches can either incorporate offline learning from known (mis-) use cases [9] or use surrogate models [15]. [33] use SAC and model augmenting for safe volt-VAR control in distribution grids.
Other applications include solutions to the optimal power flow problem [34], [35], power dispatch [36], [37], or EV charging [38]. Management of real power also plays a role in voltage control in distribution networks since conditions for reactive-reactive power decoupling are no longer met due to comparable magnitudes of line resistance and reactance.
3 Hybrid Agent Architecture and Discriminator↩︎
Our approach incorporates two policies, a world model, as well as a discriminator that chooses which policy to follow. It is part of the Adversarial Resilience Learning agent architecture [39], [40].
When an agent receives new sensor readings from the environment, usually, a policy proposes the setpoints for actuators, which are subsequently applied. In our case, we query two policies in parallel. The adaptive policy is based on SAC, the deterministic rules policy incorporates a simple voltage controller. The voltage controller is based on the following formula:
\[\label{eq:var-control} \boldsymbol{q}(t+1) = \left[\boldsymbol{q}(t) - \boldsymbol{D}(\boldsymbol{V}(t)-1)\right]^+~,\tag{1}\]
where the notation \([\cdot]^+\) denotes a projection of invalid values to the range \([\underline{\boldsymbol{q}^g}, \overline{\boldsymbol{q}^g}]\), i. e., to the feasible range of setpoints for \(q(t+1)\) of each inverter. \(\boldsymbol{D}\) is a diagonal matrix of step sizes.
As both policies return a proposal for setpoints to apply, the discriminator has to choose the better approach. It does so by querying its world model. In the simplest case, the world model is an actual model of the power grid. However, we note that the power grid model will not capture dynamics such as the behavior of other nodes or constraints stemming from grid codes (e. g., line loads or voltage gradients).
The quality of each decision proposal is quantified through the agent’s internal utility function (reward). Our reward function consists of three elements,
The world state as voltage levels of all buses: \(\boldsymbol{m}^{(t)}_{|V|}\);
The buses observed by the agent, which is subset of the world state to account for partial observability: \(\Psi\left(\boldsymbol{m}^{(t)}_{|V|}\right) \subseteq \boldsymbol{m}^{(t)}_{|V|}\);
the number of nodes controlled by agents that are still in service (i. e., unaffected by grid code violations), \(\sum_b\left\llbracket \Psi_{\Omega}\left( \boldsymbol{m}^{\left(t\right)}_{|V|}\right) \right\rrbracket_b\). Note that \(\llbracket \cdot \rrbracket\) are Iverson brackets.
To express the importance of the voltage band of \(0.90 \ge V \ge 1.10\) pu, we map the voltage magnitude to a scalar by utilizing a specifically shaped function borrowed from the Gaussian PDF:
\[G(\boldsymbol{x}, A, \mu, C, \sigma) = \frac{A}{|\boldsymbol{x}|} \cdot \sum_x \exp \left(-\frac{\left(x - \mu\right)^2}{2\sigma^2} - C \right)\] \[G_\Omega(x) = G(\boldsymbol{x}, \mu = 1.0, \sigma = 0.032, C = 0.0, A = 1.0)\]
Weights can control each part’s influence. We set \(\alpha = \beta = \gamma = \frac{1}{3}\). We construct the agent’s performance function to be:
\[\begin{gather} \label{eq:agent-performance} P_{\Omega}\left(\boldsymbol{m}^{(t)}\right) =\alpha \cdot G_{\Omega}\left(\boldsymbol{x} = \boldsymbol{m}^{(t)}_{|V|}\right)\\ + \beta \cdot \overline{G_{\Omega}\left(\boldsymbol{x} = \Psi_{\Omega}\left( \boldsymbol{m}^{\left(t\right)}_{|V|}\right)\right)}\\ +\gamma \cdot \left\{\sum_b{\left\llbracket \Psi_{\Omega}\left( \boldsymbol{m}^{\left(t\right)}_{|V|}\right) \right\rrbracket_b}\right\} {\left\{\left| \boldsymbol{m}^{\left(t\right)}_{|V|}\right| \sum_b{d^{-1}}\right\}}^{-1}~. \end{gather}\tag{2}\]
Here, the term \(\overline{\boldsymbol{x}}\) denotes the mean of \(\boldsymbol{x}\).
The agent’s performance function is normalized, i. e., \(0.0 \le P(\boldsymbol{m}{(t)}{}) \le 1.0\) in general and specifically for \(P_\Omega(\boldsymbol{m}{(t)}{})\).
The discriminator does not use the performance function value of each policy’s proposal directly. Instead, the performance values are tracked and averaged over a time period \(t\) using a simple linear time-invariant function:
\[\mathit{pt1}(y, u, t) = \left\{\begin{array}{l l} u & \quad \textrm{if \(t = 0 \)}\\ y + \dfrac{u - y}{t} & \quad \textrm{otherwise,} \end{array} \right.\]
This way, fluctuations, especially in the adaptive policy, will not lead to a “flapping” behavior; instead, the discriminator will prefer the existing controller for a longer period of time, switching to the adaptive policy only when it provides beneficial setpoints throughout a number of iterations. The dual-policy setup also treats the existing controller strategy as a fall-back, should the performance of the SAC policy drop (e. g., because of catastrophic forgetting).
The discriminator effectively causes the adaptive policy to receive three samples per step: Two projected (the proposal checked against the internal world model) and the actual reward received by the environment. As SAC is an off-policy algorithm, it can learn from all three. Hence, we effectively speed up the learning procedure.
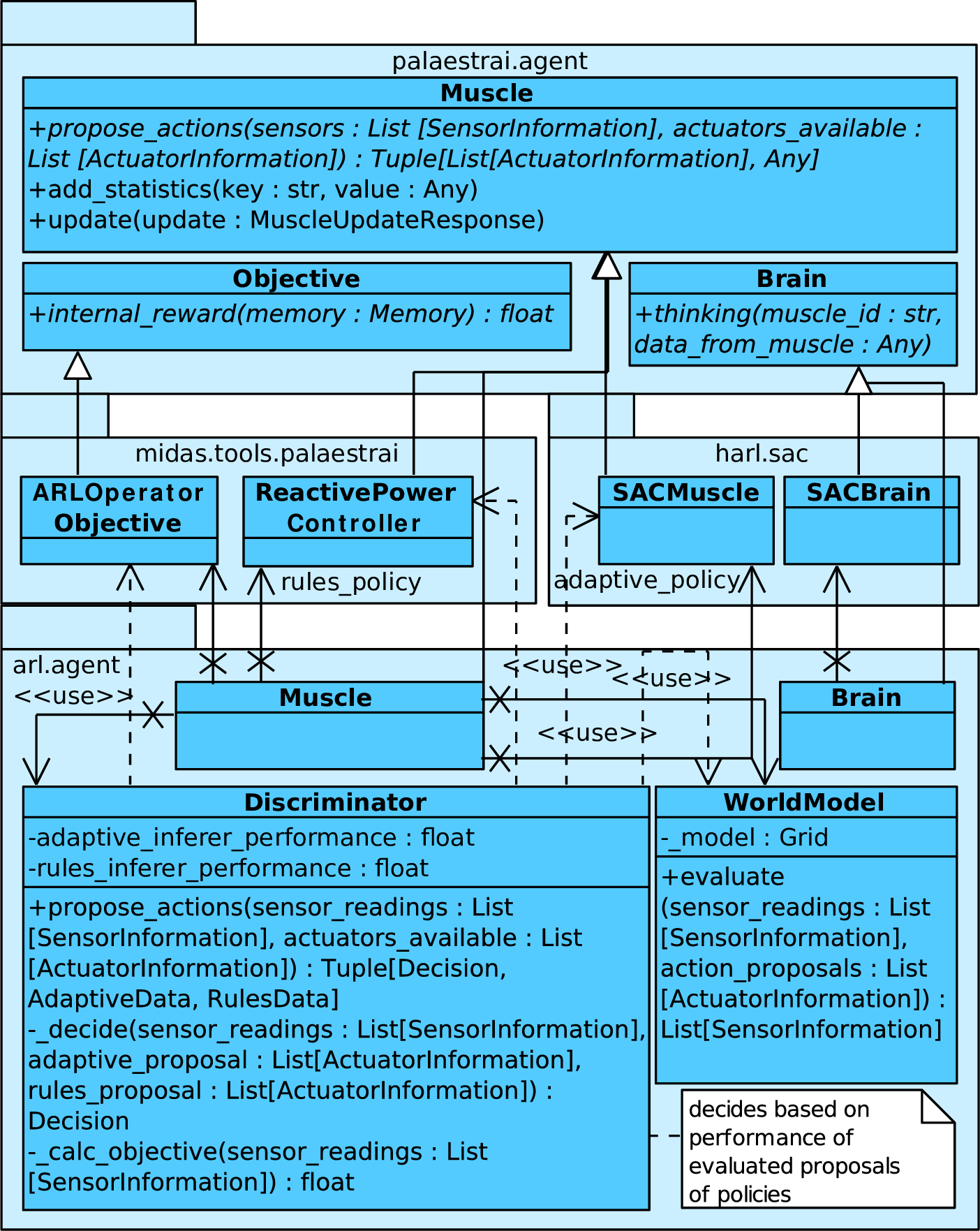
Figure 1: Class diagram of the ARL agent, featuring the Discriminator
depicts the architecture. Note that we also include the DRL rollout worker (Muscle) and learner (Brain) classes to reference traditional DRL architectures.
4 Case Study↩︎
As an approach to validate this work-in-progress state, we have chosen the CIGRÉ Medium Voltage benchmark grid. We have connected inverter-based loads and generators to each busbar. The simulation does not include additional actors, but it features constraints based on the German distribution system grid code.
The agent can control each load and generator, and is able to observe the complete grid. Note that this actually poses a challenge for DRL algorithms: Loads consume reactive power, and generators can inject it. However, an agent is able to use all actuators at once, even if this creates a conflicting situation (generating VArs and consuming them at the same time). Due to the possibility of grid code violations, the agent’s internal world model usually overestimates the reward generated by an action (cf. 2 ).
We conduct training at test runs over 5760 steps. We list all relevant parameters to the grid and hyperparameters for the SAC agents in 1. Results of the runs are depicted in 2. Here, we show a side-by-side comparison of the same voltage control task, learned and executed by a pure SAC-based agent, and by our hybrid (ARL agent) approach. We show the agent’s performance in terms of its utility function, as per 2 . For the ARL agent, we also note the policy estimates the discriminator makes based on the world model.
| Parameter | Value |
|---|---|
| Hidden Layer Dimensions | \((16, 16)\) |
| Learning Rate | \(10^{-4}\) |
| Warmup Steps | 50 |
| Training Frequency | every 5 steps |
| \(\gamma\) | 0.9 |
| Max. load per node | 1.4 MW |
| Max. reactive consumption p. n. | 0.46 MVar |
| Max. real power generation p. n. | 0.8 MW |
| Max. reactive power generation p. n. | 0.46 MVar |
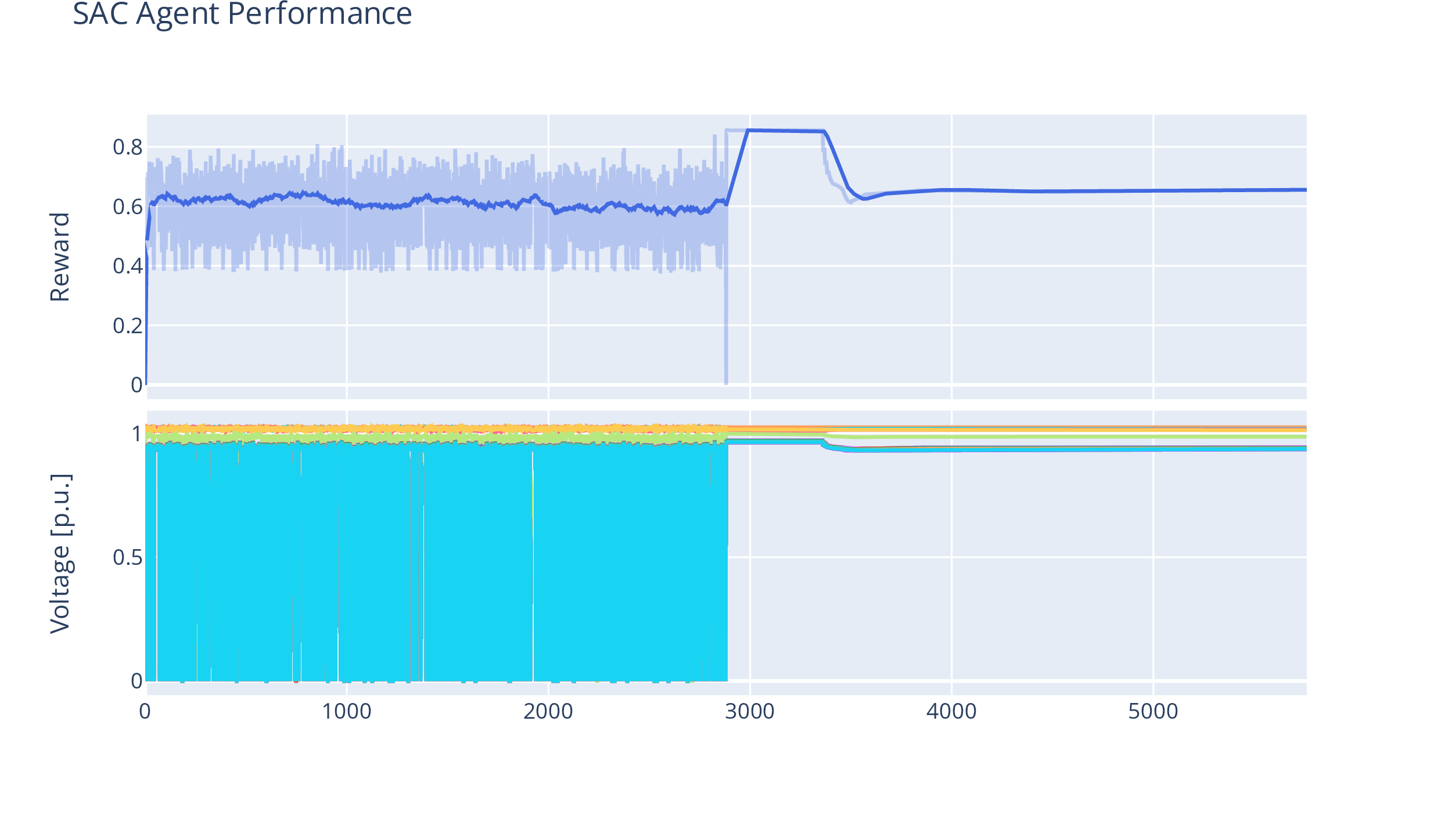
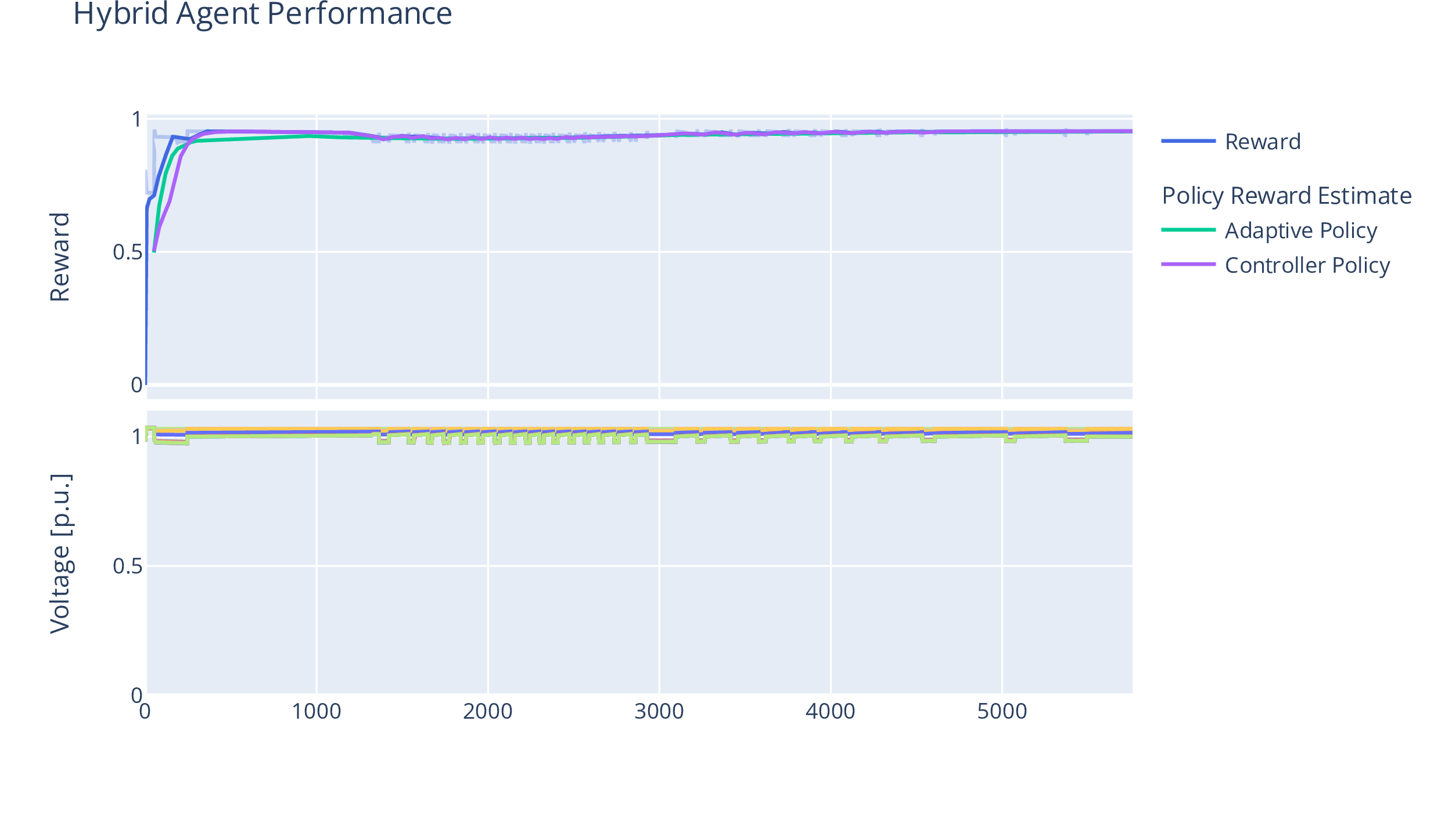
Figure 2: Utility function results (performance) and voltage magnitudes by the pure SAC agent and the Hybrid approach.
5 Discussion↩︎
Based on 2 (a), one can discern the training phase of the SAC agent and the testing phase. The fluctuations in the SAC agent’s reward curve are due to the violation of grid code constraints, which happen because of the noise and entropy bonus SAC applies during training to explore the state/action space. These violations are also visible in the voltage magnitudes plot, as buses disabled due to grid code constraints have 0 p.u. voltage magnitude In comparison , 2 ( b ) shows the results of the hybrid ( ARL ) agent approach There is no clear training/testing phase distinction visible , which is because even during training , the fallback option provided by the controller policy safeguards the agent against grid code violations For this reason , we have also plotted the internal reward estimate of the discriminator There is a gap due to the warm - up phase of the internal SAC learner ; afterward , the SAC agent learns quickly and overtakes the controller policy We note that the hybrid agent approach does not cause any grid code violations Moreover , the overestimation of the grid code ' s state does not yield any negative results We assume that this is also due to the SAC algorithm ' s explicit remedy of overestimated Q values , which was the Achilles ' heel of DDPG , and which now helps with the interaction of the world model In addition , the pure SAC agent is not able to achieve the theoretical maximum of the utility function As we noted previously , the agent has to learn the different actuators contradict each other , which the SAC implementation is not able to do during the approx 5800 steps it has to do so In contrast , the imitation learning approach of our hybrid ( ARL ) agent does so , most probably not only due to a number of “ correct ” samples provided by the controller , but also because it has thrice as many samples in its replay buffer to train on , compared to the SAC agent.
6 Conclusions & Future Work↩︎
In this paper, we described a hybrid agent approach that incorporated both, model-based DRL as well as imitation learning into a single hybrid agent architecture, which is part of the ARL agent approach. We have provided preliminary results that indicate that our approach leads to faster training as well as guarantees on the benign behavior of the agent, which is able to transparently alternate between a DRL policy and a known and tried controller policy.
In the future, we will extend our approach by testing it in more complex scenarios, adding other actors, time series for DER feed-in, more capable world models, as well as adversarial agents. As the ARL approach is a specific form of a DRL autocurriculum setup, we will evaluate the specific behavior of our approach in the face of even misactors. We will also employ methods based on DRL [41] to estimate the effectiveness of policies learned in this way. We expect that an autocurriculum approach is suitable especially to overcome adverse conditions, but has its own drawbacks in its nature of being a (model-free) DRL approach. Here, we assume that our hybrid approach will be able to bridge that gap and provide safety guarantees during normal operation, while being able to answer unexpected events by the virtue of the DRL policy.
Acknowledgement↩︎
This work was funded by the German Federal Ministry for Education and Research (BMBF) under Grant No. 01IS22071.
The authors would explicitly like to thank Peter Palensky, Janos Sztipanovits, and Sebastian Lehnhoff in their help in establishing the ARL research group.
References↩︎
The tutorial by [28] is available only as a preprint. However, to our knowledge, it constitutes one of the best introductory seminal works so far. Since it is a tutorial/survey and not original research, we cite it despite its nature as a preprint and present it alongside the peer-reviewed publication by [27], which cites the former, too.↩︎

