Are Doppler Velocity Measurements Useful for Spinning Radar Odometry?
April 02, 2024
Abstract
Spinning, frequency-modulated continuous-wave (FMCW) radar has been gaining popularity for autonomous vehicle navigation. The spinning radar is chosen over the more classic automotive ‘fixed’ radar as it is able to capture the full \(360\si{°}\) field of view without requiring multiple sensors and extensive calibration. However, commercially available spinning radar systems have not previously had the ability to extract radial velocities due to the lack of repeated measurements in the same direction and fundamental hardware setup. A new firmware upgrade now makes it possible to alternate the modulation of the radar signal between azimuths. In this paper, we first present a way to use this alternating modulation to extract radial Doppler velocity measurements from single raw radar intensity scans. We then incorporate these measurements in two different modern odometry pipelines and evaluate them in progressively challenging autonomous driving environments. We show that using Doppler velocity measurements enables our odometry to continue functioning at state-of-the-art even in severely geometrically degenerate environments.
1 Introduction↩︎
Range-measuring sensors, such as radar and lidar, are now commonly used for many autonomous vehicle tasks such as adaptive cruise control, crash warning systems, and odometry and localization. Lidar is generally regarded as the more accurate of the two, owing to its ability to capture returns from the full 3D environment at a high rate and accuracy [1]. On the other hand, radar tends to have a longer range and is essentially unaffected by heavy precipitation. Additionally, radar has traditionally been the only sensor able to use the Doppler effect to estimate radial velocities of objects. Although there have been recent advancements in FMCW lidar sensors that are able to achieve this task [2], these sensors are still relatively uncommon. As a result, there has been a recent increase in work attempting to leverage the unique advantages of radar [3].

Figure 1: Data collection platform Boreas in front of the Burlington Bay James N. Allan Skyway, which has almost no geometric features.
Autonomous vehicles typically use frequency-modulated continuous-wave (FMCW) automotive or spinning radar. Automotive radar directly provides the range, radial cross section, elevation, and radial velocity of targets, but is only capable of operating on a limited, fixed field-of-view (FOV) [4]. On the other hand, spinning radar provides a full \(360\si{°}\) FOV coverage, but has previously only returned the range and intensity of targets [5]. Spinning radar can support autonomy tasks, such as odometry and localization, where a high degree of accuracy and awareness of all vehicles on the road is sought [6]. Using multiple automotive radars for the same task would instead require several sensors and extensive calibration. Additionally, most automotive radars directly provide extracted features instead of raw signal returns. This makes it harder to fine-tune the feature extraction process for specific odometry, mapping, or localization tasks.
Further improving the capabilities of spinning radar, Navtech spinning radars have recently made it possible to extract Doppler velocity measurements. This follows from the new ability to have a negatively sloped radar signal modulation. These Doppler-enabled radar systems, referred to as ‘spinning Doppler radar’, alternate their modulation pattern per azimuth, first increasing it for one azimuth and then decreasing it for a subsequent one. However, unlike with automotive radar, Doppler velocities are not directly provided. Additionally, automotive radar provides highly accurate Doppler measurements on account of many repeated measurements of the same target [7]. In contrast, spinning radar only has a small overlap between consecutive azimuths, meaning that at best, a target is present in only two to three measurements per rotation. Thus, despite it being theoretically possible to extract Doppler measurements for spinning radar, it is unclear if they are sufficiently good enough to be useful. This paper thus aims to answer the question ‘are Doppler measurements useful for spinning radar navigation?’
Previously, [8] used Doppler measurements for a radar localization and mapping using a custom Doppler-enabled spinning radar. More recently, [9] made use of the Doppler information from a Navtech CTS350-X radar to train a neural network to directly predict vehicle pose information. However, they do not directly extract the Doppler velocity information, which makes it hard to evaluate its quality and impact. Additionally, both works halved the number of azimuths in order to extract Doppler information, and, in part because of this, do not produce results that are on par with modern state-of-the-art radar odometry approaches. We are thus revisiting the analytical approach presented in [8] and refining it using our continuous-time state estimation techniques. As shown in [9] and our own experiments, halving the resolution decreases performance of spinning radar odometry. We thus provide an approach to retain the full resolution while still extracting Doppler velocities. We evaluate our approach, and the usefulness of Doppler measurements, on a dataset collected in progressively challenging environments ranging from a suburb to the geometrically degenerate skyway shown in Figure 1.
The contributions of this paper are thus:
We present a method to extract Doppler velocities using spinning radar, which improves on the prior work by [8].
We demonstrate that these Doppler velocity measurements are useful by incorporating them in two odometry pipelines: one that maximizes computational speed and another that maximizes performance.
The rest of the paper is organized as follows. Section 2 contextualizes the novelty claim. Section 3 discusses necessary radar theory and our Doppler velocity extraction approach. Section 4 presents the dataset, evaluated pipelines, and experimental results. Finally, Section 5 concludes the paper and discusses future extensions.
2 Related Work↩︎
2.1 Spinning Radar Navigation↩︎
Spinning radar navigation has recently seen a surge of interest [3], [10], [11]. Odometry and localization methods have typically been split into iterative closest point (ICP)-style pointcloud matching approaches [12]–[14], scan matching approaches [15], [16], and feature matching approaches [17], [18]. These have largely ignored Doppler-based distortion, and, owing to the limitations of previously available hardware, have not extracted Doppler measurements directly. In our previous work, we looked at correcting Doppler distortion in a spinning radar through the use of the vehicle ego-motion velocity estimate [19].
2.2 Automotive Doppler Radar↩︎
[6] showed the ability of an automotive Doppler radar sensor to produce usable ego-motion estimates in combination with an Ackerman vehicle model. They do this by finding a least-squares fit to the measured point-wise radial Doppler velocities from points deemed stationary by Random Sample and Consensus (RANSAC) [20]. They also provide a study using simulated data about the impact of the number of detected targets, the accuracy of measured radial velocity and azimuth, and the number of outliers on the quality of the estimated velocity. Interestingly, they note that azimuth accuracy is less important than velocity accuracy. Additionally, they show that the ego-motion estimation fails in the presence of many non-stationary targets, such as can be expected in heavy road traffic. This work is extended in [21], where multiple radars are used in order to relax the requirement for a vehicle model; this is the first paper to show full 2D vehicle ego-motion estimation entirely using radar sensors. More recently, [22] showed that Doppler measurements from an automotive radar can be used to do full 3D odometry by again using RANSAC and a kinematic model. Instead of using RANSAC, [23] developed a dynamic object outlier rejection scheme using the previous ego-vehicle estimate. [4] used Doppler measurements to undistort radar points in an uncertainty-aware way before using them in a probabilistic descriptor-based localization approach.
2.3 Spinning Doppler Radar↩︎
There have been two previous works that have used Doppler measurements from spinning radar. [8] developed a custom Doppler-enabled spinning radar and used it for the task of localization and mapping of a small mobile platform in simple outdoor environments. Our Doppler extraction approach is most similar to theirs, as both use cross-correlation. However, our extraction approach makes use of an additional filtering step, which we found crucial to reach velocity estimates that were sufficient in an autonomous driving context. Additionally, for a radar scan composed from \(N\) azimuths, our extractor produces \(N-1\) velocity estimates as compared to their \(N/2\). Finally, their experiments were conducted in relatively slow (\(\leq 8.5 \si{\meter}/\si{\second}\)) conditions without dynamic objects in the scene. We provide more extensive experimental results in multiple real autonomous driving environments, with speeds reaching up to \(28 \si{\meter}/\si{\second}\).
On the other hand, [9] used a modern, commercially available radar to estimate the vehicle ego-motion from the Doppler effect. This radar is functionally the same to the one that we use. However, their approach is entirely learning-based, as they feed their raw scans into a neural network to directly estimate the change in vehicle pose. They thus never directly extract Doppler measurements or estimate the ego-vehicle velocity explicitly. We propose an analytical method to extract Doppler velocities, and show how they can be used in different ways to correct the ego-vehicle velocity, and, ultimately, position.
2.4 Doppler Lidar↩︎
It is also worth noting the development of FMCW lidar sensors, as they are also capable of providing Doppler measurements that have historically been unique to radar [24]. These sensors have thus far been limited to a fixed FOV, not unlike automotive radar. Doppler measurements from a commercially available FMCW lidar were shown to be effective at preventing ICP algorithm failure in degenerate geometric environments [2]. They were also shown to be useful in continuous-time odometry ICP [25] and at fast, correspondence free velocity estimation [26]. We evaluate similar pipelines using a spinning radar in our experiments, with a direct comparison between Doppler-enabled radar and lidar left for future work.
3 Methodology↩︎
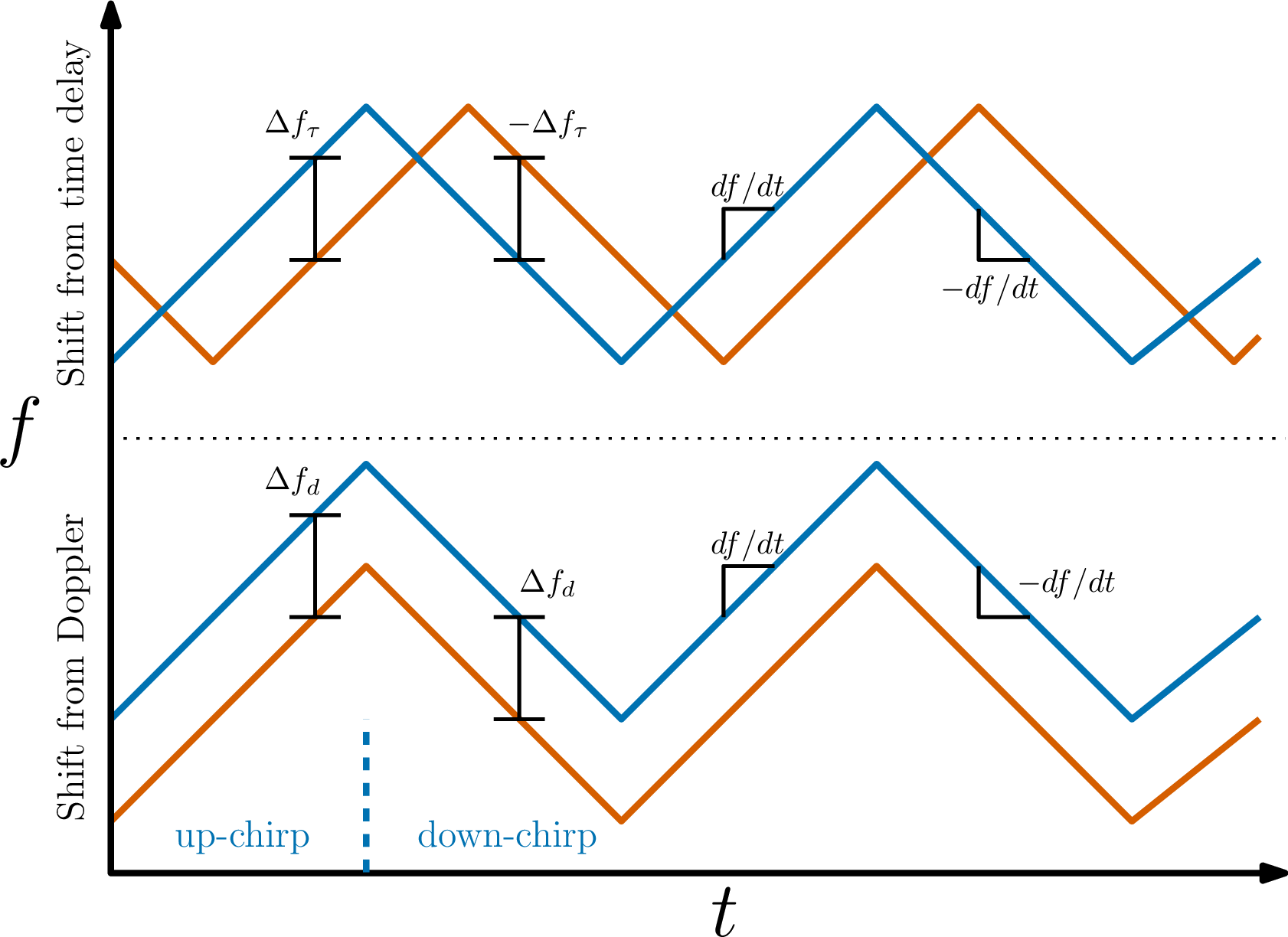
Figure 2: A graphical representation of the shift in the frequency between the transmitted signal in blue and the received signal in orange for an FMCW radar with an alternating modulation pattern. The top shows a frequency shift \(\Delta f_\tau\) resulting from a time delay induced by the signal traveling some distance. The bottom shows a frequency shift \(\Delta f_d\) resulting from the Doppler effect of an object moving away from the radar. The slope of the signal modulation \(df/dt\) is also shown.
3.1 Spinning Doppler Radar Theory↩︎
FMCW radar determines the range \(r\) to a target based on the difference between the received \(f_r\) and transmitted \(f_t\) signal frequencies, \(\Delta f = f_r - f_t\): \[\begin{align} \label{eq:r95basic} r = \frac{c \Delta f}{2 (df/dt)}, \end{align}\tag{1}\] where \(c\) is the speed of light, \(df/dt\) is the slope of the modulation pattern, and the division by 2 is present since the signal has to travel to and from the target. The difference in frequencies arises from two factors: the time delay corresponding to the signal travelling to and from an object, and a Doppler-induced compression or expansion of the signal from the relative motion of a target. These two cases are visualized in Figure 2 for the case of an alternating modulation signal, where \(df/dt\) is first positive (‘up chirp’) and then negative (‘down chirp’) in alternating fashion. When only a time delay shift \(\Delta f_\tau = f_\tau - f_t\) is present, 1 is equal and constant regardless of which signal modulation was transmitted, since the negatives in the \(\Delta f\) and \(df/dt\) cancel out for the down chirp. However, in the case of a Doppler-induced shift \(\Delta f_d = f_d - f_t\), the range measurement will be impacted in opposite ways. This happens because the shift is constant for both chirp types, whereas the slope of the modulation has a flipped sign. This opposite shift is visually shown in Figure 3, where azimuths alternate between up and down chirp types, creating a ‘zig-zag’ effect in what should be flat features. The opposite offset allows us to extract the Doppler velocity \(u\), which is connected to \(\Delta f_d\) through the wavelength of the transmitted signal \(\lambda_t\) as \[\begin{align} \Delta f_d = \frac{2u}{\lambda_t}. \end{align}\] Combining both types of shifts, the measured range from an up chirp is \[\begin{align} r_\mathrm{up} = \frac{c \Delta f_\tau}{2 (df/dt)} + \frac{c \Delta f_d}{2 (df/dt)} = \tilde{r} + \Delta r_d, \end{align}\] where \(\tilde{r}\) is the true range to the target and \(\Delta r_d\) is the Doppler-induced range shift. For the down chirp, the range is \[\begin{align} r_\mathrm{down} = \frac{-c \Delta f_\tau}{2 (-df/dt)} + \frac{c \Delta f_d}{2 (-df/dt)} = \tilde{r} - \Delta r_d. \end{align}\] If a range measurement from both chirp types is known, we have a system of two equations with two unknowns, which allows us to solve for \(\Delta r_d\), and consequently \(u\), as \[\begin{align} \Delta r_d &= \frac{c \Delta f_d}{2 (df/dt)} = \frac{2 c u}{2 \lambda_t (df/dt)}, \\ u &= \frac{\Delta r_d (df/dt)}{f_t} = \frac{\Delta r_d}{\beta}, \end{align}\] where \(\beta = f_t/(df/dt)\).
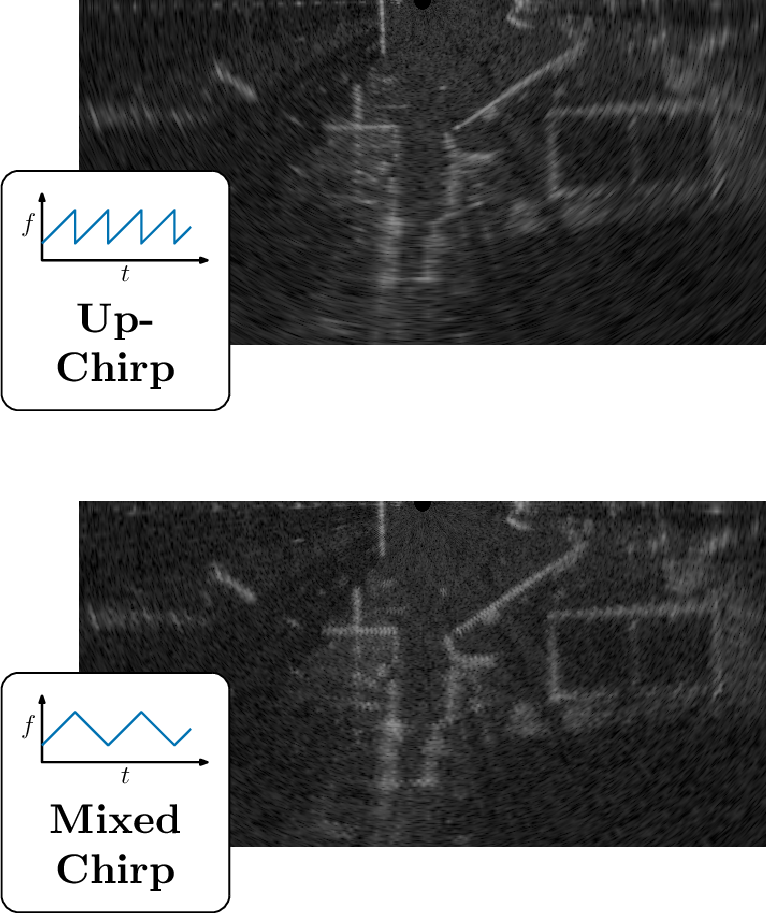
Figure 3: Bottom half of an up-chirp (top) and mixed chirp (bottom) raw radar intensity image transformed into Cartesian coordinates captured from a moving radar. The Doppler-induced shift produced by the alternating signal modulation from one azimuth to another can be seen as a ‘zig-zag’ in the intensity returns of the bottom image.
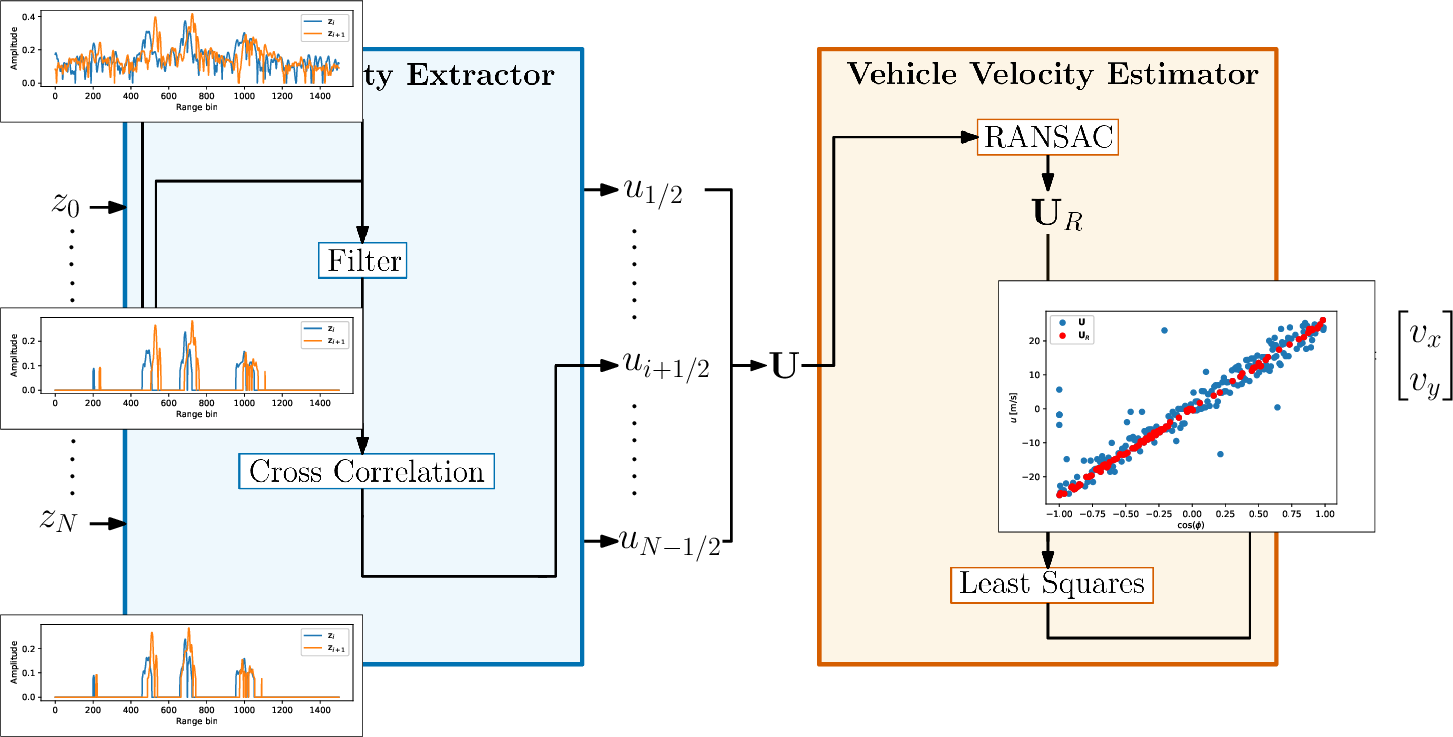
Figure 4: The Doppler velocity estimation pipeline. First, raw radar intensity azimuths \(\mathrm{z}_k, k \in{0, N}\) are loaded into the radial velocity extractor. For each consecutive pair of azimuths, the extractor first filters the signals, and then runs a cross-correlation based on which a radial velocity \(u_j, j \in \{1/2, N-1/2\}\) is computed. Radial velocities for the entire scan \(\mbf{U}\) are passed through RANSAC to determine inliers, and then used in a least squares algorithm to estimate the ego-vehicle velocity \(\mbf{v}\).
3.2 Doppler Velocity Extraction↩︎
The quantity that we are interested in extracting is the Doppler velocity measurement \(u\) for each point. To do so, we need to find the Doppler-induced range offset, \(\Delta r_d\). However, to solve the system of two equations, we need to obtain range measurements from up and down chirp signals. In our case, where azimuths alternate in chirp type, this would involve identifying which points from consecutive azimuths correspond to the same target. An alternative, entirely association-free way to find the \(\Delta r_d\) is to instead consider the entire azimuth at once. If we assume that consecutive azimuths are looking at mostly the same targets, then the entire return signals will be shifted by \(\Delta r_d\) in the corresponding direction. Thus, a cross-correlation between consecutive return signals would return the distance shift between the signals, which would correspond to \(2\Delta r_d\). The downside of this is that each azimuth is assigned a single radial velocity. However, the Doppler measurement is then extracted without needing to ever extract or match explicit points in the return signals. Additionally, it can be done at the same time as azimuths arrive, without needing to wait for a full scan to complete.
Unfortunately, since there are only two return signals, the cross-correlation on the raw signals is very noisy and error-prone. Thus, a signal filtering step is first taken. We find that a modified version of the filtering approach previously applied to radar pointcloud extraction in [12] was highly effective in pre-processing the signals for cross-correlation matching. Specifically, our filtering approach is as follows:
Subtract the mean.
Estimate the variance of the signal noise based on negative signal values (see [12] for more details).
Apply a Gaussian filter.
Re-weight the smoothed signal by the probability that each bin does not correspond to noise (see [12] for more details).
We hypothesize that the success of this filtering approach for cross-correlation lies in the smoothing out of signal kinks to find the underlying low-frequency signal, and then the reintegration of the high-frequency signal through the high-frequency noise re-weighting step. After filtering of both azimuths, a standard cross-correlation between the signals is performed to produce \(\Delta r_d\) and consequently \(u\). The radial velocity is assigned to the average azimuth value of the two considered azimuths. Since we compute one radial velocity measurement for each unique pair of \(N\) azimuths, we acquire \(N-1\) radial velocity measurements. This is in contrast to previous spinning Doppler radar works [8], [9] where the number of used azimuths was halved, since the other half was used to generate Doppler measurements. This process is shown in the radial velocity extractor block of Figure 4.
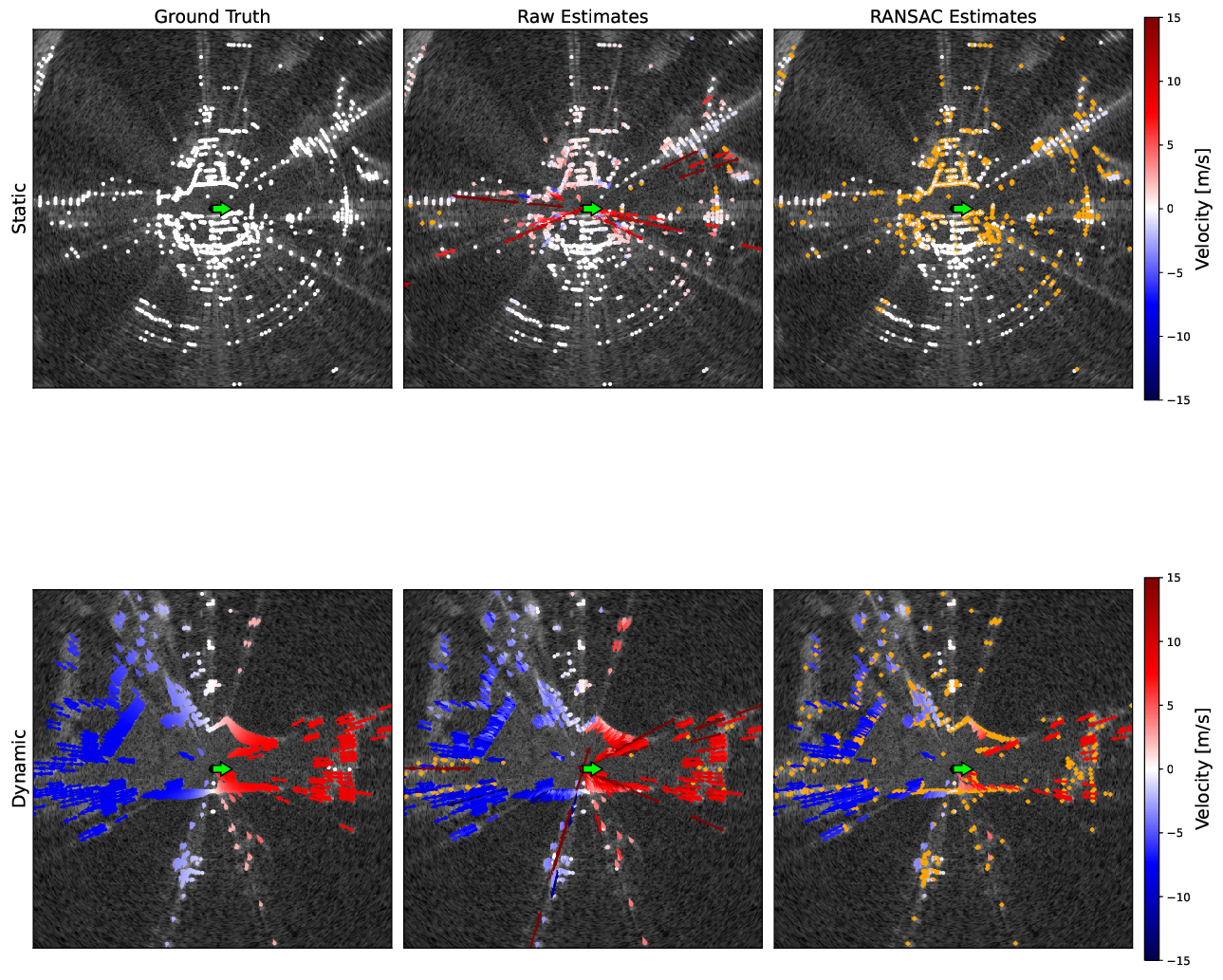
Figure 5: Groundtruth and estimated radial velocities projected onto a pointcloud extracted from a raw radar scan in a static and dynamic scene. Velocities shown in the raw estimates column correspond to the initial association-free Doppler velocity estimation. Velocities shown in the RANSAC estimates column correspond to RANSAC-processed velocities, with rejected velocities coloured in orange. The vehicle orientation is shown as a green arrow.
3.3 Velocity Pseudo-Measurement Estimator↩︎
In general, the Doppler velocity extraction is prone to outliers and produces velocities with a relatively high distribution about the true value. To produce an ego-vehicle velocity pseudo-measurement, we combine all radial velocity measurements in an estimator. This is visualized in the vehicle velocity estimator block of Figure 4.
First, we use RANSAC with a relatively loose outlier rejection threshold to filter out erroneous cross-correlation results and azimuths that correspond to dynamic objects. In environments where very few environmental points are present, it is easy for RANSAC to instead latch onto the dynamic objects in the scene. To overcome this issue, we include a very loose prior to the RANSAC model. This prior discards RANSAC candidates that deviate too far, more than \(6 \; \si{\meter\per\second}\) specifically, from the previous velocity estimate, even if that candidate has a large number of inliers. We find that this is sufficient to mitigate the ‘capture’ of the velocity estimate by a large number of dynamic objects in the scene, without restricting our estimator. This is reminiscent of the approach taken in [23], although we make use of both the velocity from a previous timestep and RANSAC, whereas they forgo RANSAC.
After RANSAC, the inlier azimuth velocities are fed to a least-squares (LS) algorithm with a Cauchy loss. The LS algorithm estimates the forward \(v_x\) and side \(v_y\) ego-vehicle velocities as \[\begin{align} \mbf{v} = \begin{bmatrix}v_x \\ v_y \end{bmatrix}. \end{align}\] This approach generates a single ego-vehicle velocity estimate per radar scan, to which we assign a timestamp corresponding to the middle of the scan. This assumes a constant acceleration throughout the scan, with radial velocity errors at the start and end contributing equally in opposite directions to the estimate of the ego-vehicle velocity at the middle timestamp. In the future, we are looking to implement a continuous-time estimator to properly account for the timestamp at which each azimuth is received. Since most radar systems return only a few hundred azimuths (400 for the Navtech CIR350-X used in our experiments), this estimation is extremely fast. Although we find that using a Cauchy loss is necessary for best performance, depending on the requirements of the application it may be sufficient to simply use a standard LS algorithm. In this case, the estimation problem becomes linear in \(\mbf{v}\), meaning that it can be solved in one step.
Figure 5 shows a qualitative result of the pipeline. In the figure, estimated azimuths are projected onto points extracted using the BFAR extractor [27] for visual clarity. The groundtruth radial velocities are generated by projecting the groundtruth vehicle velocity into each azimuth. It can be seen that the raw extracted radial velocities have strong outliers, which are removed using RANSAC.
4 Experiments↩︎

Figure 6: A camera image and radar scan from each of the four trajectory types. The increase in difficulty for radar odometry from left to right can be observed in the fewer distinct geometric features.
4.1 Considered Pipelines↩︎
4.1.1 Radar ICP Baseline↩︎
One baseline pipeline with two operating modes is considered. The pipeline is based on the Teach and Repeat framework [28] and is identical to the one used in [13]. Radar scans are used to extract pointclouds, which are then fed to ICP to produce an odometry estimate. The \(SE(2)\) pose and \({\boldsymbol{\varpi}} = \begin{bmatrix}v_x & v_y & \omega \end{bmatrix}^{\mathsf{T}}\) ego-vehicle body velocity are estimated in continuous time. A white-noise-on-acceleration prior is used. Please refer to [13] for full details. For simplicity, this pipeline is referred to as ‘Radar ICP’.
Two modes of Radar ICP are considered. First, Radar ICP without any Doppler corrections is run as a baseline. Second, Radar ICP is run with Doppler corrections generated using the estimated ego-vehicle velocity. In this mode, the ego-velocity estimate is used to compute the Doppler-induced \(\Delta r_d\) shift in the range measurements, and extracted points are corrected by the corresponding amount. This approach was shown to improve performance in [19].
4.1.2 Doppler Radar ICP↩︎
The first novel radar odometry pipeline, referred to as ‘Doppler Radar ICP’, simply adds a Doppler measurement-based term to Radar ICP. As discussed in Section 3.3, the Doppler measurement estimator is used to estimate a forward and side ego-vehicle velocity \(\mbf{v}\) for the timestamp at the midpoint of each scan. This estimate is then included as an additional cost term in the Radar ICP pipeline by querying the continuous velocity estimate at the scan midpoint timestamp and contrasting it with \(\mbf{v}\). A fixed noise covariance is tuned for this loss term. This pipeline is relatively slow owing to the iterations needed for ICP, but should theoretically grant state-of-the-art performance.
4.1.3 Doppler Radar + Gyroscope↩︎
The second novel radar odometry pipeline, referred to as ‘Doppler Radar + Gyro.’, is adapted from [26] and directly integrates Doppler-based linear velocity pseudo-measurements and gyroscope measurements to estimate a pose. Currently, this is done very coarsely by simply taking one Doppler-based pseudo-measurement and one gyroscope measurement per radar scan and integrating them forward by the timestep needed to reach the next frame. This pipeline is extremely fast, but is highly dependent on the quality of the gyroscope for performance.

Figure 7: Average percent odometry drift for different algorithms on increasingly difficult trajectories. Results are averaged over four sequences for each trajectory type.
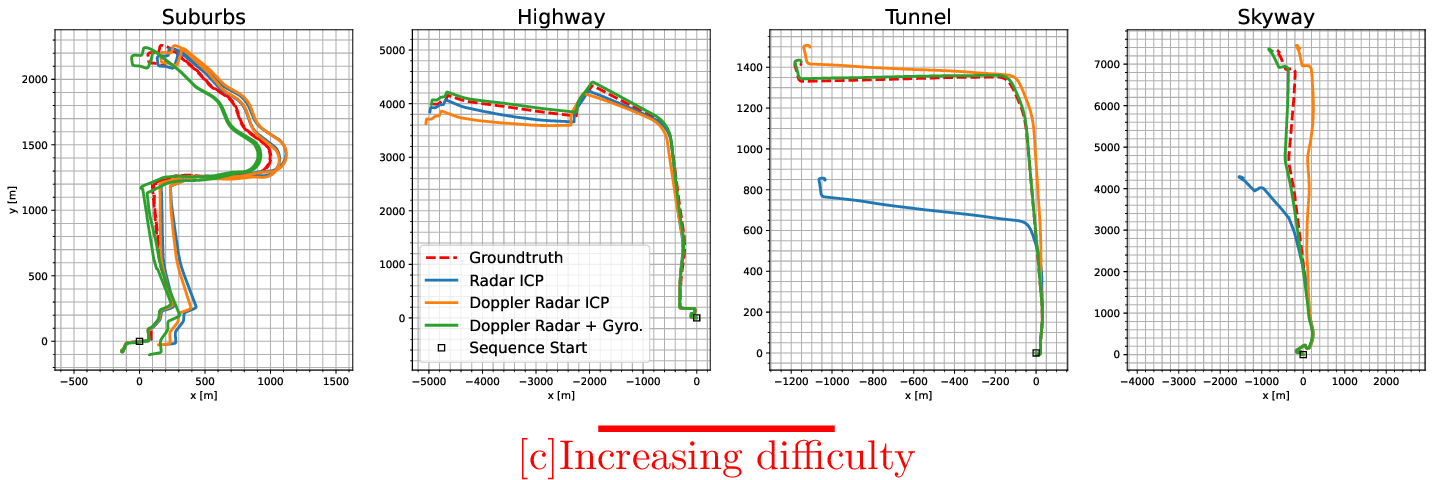
Figure 8: Visualization of odometry performance for one sequence from each of the four types of trajectories. The baseline Radar ICP with Doppler corrections algorithm is shown alongside the two new algorithms making use of spinning radar Doppler measurements. Groundtruth is shown as a red dotted line. The trajectories are presented in increasing order of difficulty from left to right. The new methods perform on par with the baseline in the two easiest cases, and continue to provide valid odometry results in the two harder cases where the baseline fails.
4.2 Dataset↩︎
We used the Boreas platform [5] to collect Doppler-enabled spinning radar data in progressively more challenging environments. We used the Navtech CIR350-X spinning radar, which operates between 76 and 77 \(\si{\giga\hertz}\) with a range resolution of \(\approx 4.3 \; \si{\cm}\). The radar spins at 4 \(\si{\hertz}\) and generates 400 azimuth measurements per rotation. The signal has a \(3 \; \si{\decibel}\) beamwidth of \(1.8\si{°}\), meaning that consecutive azimuths overlap by \(0.9\si{°}\). This overlap lets us make the approximation that consecutive signals have returns from the same targets. The groundtruth is generated using post-processed GNSS, 6 degree of freedom IMU, and wheel encoder measurements from Applanix’s RTX POSPac software.
One caveat with regards to the ‘Doppler Radar + Gyro.’ results is that the gyroscope data is the same one that is used for post-processing the groundtruth, as there was no other gyroscope on board the platform.2 We use the raw gyroscope data in our direct integration algorithm, but it is nonetheless a very high quality, essentially unbiased gyroscope and thus introduces little drift.
We collected four repeated runs on four progressively difficult sequences:
Suburbs (easy): These sequences follow the suburban Glen Shields route from [5] with speed limits of \(30-60 \; \si{\km\per\hour}\). All parts of the trajectory have multiple visible and unique geometric features.
Highway (medium): These sequences start in a suburban environment and then exit onto a highway with speed limits up to \(80 \; \si{\km\per\hour}\). Parts of the highway are geometrically challenging with only roadside barriers visible.
Tunnel (hard): These sequences drive through the \(840 \; \si{\meter}\) long Thorold Tunnel in St. Catherines, Ontario, before turning onto a country road. The speed limit is up to \(80 \; \si{\km\per\hour}\). The inside of the tunnel is consistently geometrically degenerate, with only two continuous parallel walls visible.
Skyway (hard): These sequences traverse the \(2,560 \; \si{\meter}\) long Burlington Bay James N. Allan Skyway in Burlington, Ontario, with speed limits of up to \(100 \; \si{\km\per\hour}\). The skyway has large stretches with almost no visible static features, but many vehicles visible directly in front and behind the car. The static features that do exist are repetitive and only present to the sides of the car.
4.3 Odometry Results↩︎
The odometry drift from the considered pipelines is presented in Table 7. The drift is reported as an average value of the KITTI-style odometry metrics [29] from subsequences of length (100, 200, …, 800). The results across each of the four sequences for each sequence type are then averaged to generate the final performance metric. We omit rotational drift values for brevity and because they show similar trends. A visualization of the odometry performance for one sequence from each sequence type is shown in Figure 8.
It can be seen that all ICP-based methods drop in performance as the geometric difficulty of the sequences increases. For the two considered baselines, the estimation pipeline fails entirely as soon as the car enters the tunnel or skyway. Both new pipelines that incorporate Doppler measurements continue to produce functional odometry results regardless of the type of sequence. Interestingly, directly integrating Doppler and gyroscope measurements performs the best from all the pipelines in the hard environments, and on par in the easy and medium cases. This highlights the value that even a 1DOF gyroscope brings to an estimation pipeline, which we have similarly noted in our previous work [26], [30]. An additional interesting finding is in the large improvement in performance between the two baselines. Compared to the results from [19], we see a large improvement in odometry when compared to Doppler compensation based on the ego-vehicle velocity. It is hypothesized that the improvement in performance is owed to the added difficulty of running ICP on pointclouds with alternating positive and negative Doppler shifts. If all points are shifted in the same direction, as was the case in [19], ICP seems to be almost unaffected.
5 Conclusion↩︎
This paper shows the feasibility of analytically extracting and making use of Doppler velocity measurements in a modern radar odometry pipeline. We test our proposed approach in four different, progressively more challenging environments: suburbs, highway, tunnel, and skyway. The use of these measurements allows a pipeline to perform on par in easy geometric environments, and to maintain a good level of performance in geometrically degenerate situations where the baseline completely fails. We show this in both an ICP-based, radar-only pipeline and in a fast ego-velocity estimation pipeline, where odometry results are generated by directly integrating Doppler-based linear velocity and a gyroscope.
Future extensions to the work presented here will include evaluating the impact of Doppler measurements on mapping and localization, outlier rejection, and object tracking.
References↩︎
arXiv:2302.07433, 2023.arXiv:2305.01135, 2023.arXiv:2310.04113, 2023.arXiv:2109.09669, 2021.arXiv:2402.06174, 2024.All authors are with the University of Toronto Institute for Aerospace Studies (UTIAS), 4925 Dufferin St, Ontario, Canada. {daniil.lisus, keenan.burnett, david.yoon, tim.barfoot}robotics.utias.utoronto.ca?↩︎
We plan to integrate a separate heading gyroscope in the future.↩︎