Abstract
Rapid advances in the field of Large Language Models (LLMs) have made LLM-based code generation an important area for investigation. An LLM-based code generator takes a prompt as input and produces code that implements the requirements specified in the prompt. Many software requirements include mathematical formulas that specify the expected behavior of the code to be generated. Given a code generation prompt that includes a mathematical formula, a reasonable expectation is that, if the formula is syntactically modified without changing its semantics, the generated code for the modified prompt should be semantically equivalent. We formalize this concept as syntactic robustness and investigate the syntactic robustness of GPT-3.5-Turbo and GPT-4 as code generators. To test syntactic robustness, we generate syntactically different but semantically equivalent versions of prompts using a set of mutators that only modify mathematical formulas in prompts. In this paper, we focus on prompts that ask for code that generates solutions to variables in an equation, when given coefficients of the equation as input. Our experimental evaluation demonstrates that GPT-3.5-Turbo and GPT-4 are not syntactically robust for this type of prompts. To improve syntactic robustness, we define a set of reductions that transform the formulas to a simplified form and use these reductions as a pre-processing step. Our experimental results indicate that the syntactic robustness of LLM-based code generation can be improved using our approach.
syntactic robustness, gpt, code generation, LLM models.
1 Introduction↩︎
Large language models (LLMs), especially ChatGPT, are becoming immensely popular for code generation. Astonishingly, the accuracy of GPT-4-based code generation techniques is as high as 96% for the HumanEval dataset [1]. Recent works have also argued for the potential use of LLMs for code generation of safety-critical software in order to “improve software safety and development efficiency” [2]. With its increasing adoption, there is a pressing need to evaluate the correctness and reliability of LLM-based code generation. The early adopters of ChatGPT as a code generation tool have already demonstrated this need [3].
One common approach for assessing reliability in machine learning systems is robustness; robustness for neural networks trained for classification is extensively studied but there is much less work on robustness for generative AI models. Robustness for classification models is measured by defining a neighborhood around an input which is expected to not change the classification and testing or formally verifying the classifications within that neighborhood [4]. However, this definition must be altered for a generative model, as an objectively accurate output may not exist for a given input. In this paper, we define a novel concept of robustness for LLM-based code generators, which are a subdomain of the generative models.
Prior works have demonstrated the necessity for achieving robustness in code generation with LLMs [2], [5]. As suggested in [6], robustness for code generation with LLMs is a degree to which similar prompts elicit semantically and syntactically similar codes. However, this definition does not capture the syntactic variations of generated code as it is possible to write multiple correct code solutions to a given problem. In this case, for a given code generation prompt, syntactically, there can be more than one way to generate the code that correctly answers the given prompt.
We propose a novel definition of robustness for LLM-based code generation called syntactic robustness. Informally, we define syntactic robustness as the degree to which the semantically equivalent prompts elicit semantically equivalent responses. In other words, code generation by an LLM is syntactically robust when, given two syntactically different but semantically equivalent prompts, the LLM responds with generating semantically equivalent programs. We introduce a formal definition of syntactic robustness in this paper (Section 3).
Numerical analysis plays a significant role in solving various computationally hard problems such as scientific simulations, operational research modeling, etc. The algorithms developed for numerical analysis often incorporate solving mathematical formulas [5]. These formulas serve as an excellent benchmark to evaluate our definition of syntactic robustness, as there can be syntactically more than one way to represent a mathematical formula. According to our definition of syntactic robustness, we expect the code generated by the LLMs to yield equivalent solutions for syntactically different representations of the same formula.
After showing examples that demonstrate that GPT-3.5-Turbo (hereafter called GPT-3.5) is not syntactically robust (Section 2), we present a prompt generation technique for evaluating the syntactic robustness of LLM-based code generation (Section 4). We focus on linear, quadratic, trigonometric, and logarithmic equations for our analysis based on the most commonly used mathematical formulas in numerical analysis. Further, we formally define syntactic transformations that generate syntactically different but semantically equivalent variations of the mathematical formulas. We use these variations, called mutations (Section 5), to evaluate the syntactic robustness of LLM-based code generators.
Once it is established that a given LLM used for code generation is not syntactically robust, we introduce an approach for prompt reduction as a pre-processing step to improve its syntactic robustness. Our prompt reduction technique uses syntactic transformations (called reductions) that continually reduce the formula size until a fixed point is reached (Section 6). We present an experimental evaluation that demonstrates that GPT-3.5 and GPT-4 are not syntactically robust, but they achieve 100% syntactic robustness when combined with a pre-processing step that generates reduced mathematical formulas. Our contributions in this paper can be summarized as follows:
A formal definition of syntactic robustness.
A prompt pre-processing technique that significantly improves the syntactic robustness of LLMs.
A set of code generation prompts based on linear, quadratic, trigonometric, and logarithmic equations, and a set of formula mutation rules that together can be used for syntactic robustness testing.
A workflow for testing and analysis of syntactic robustness of LLM-based code generators.
Empirical evaluation and analysis of syntactic robustness of GPT-3.5 and GPT-4.
2 Motivation and Overview↩︎
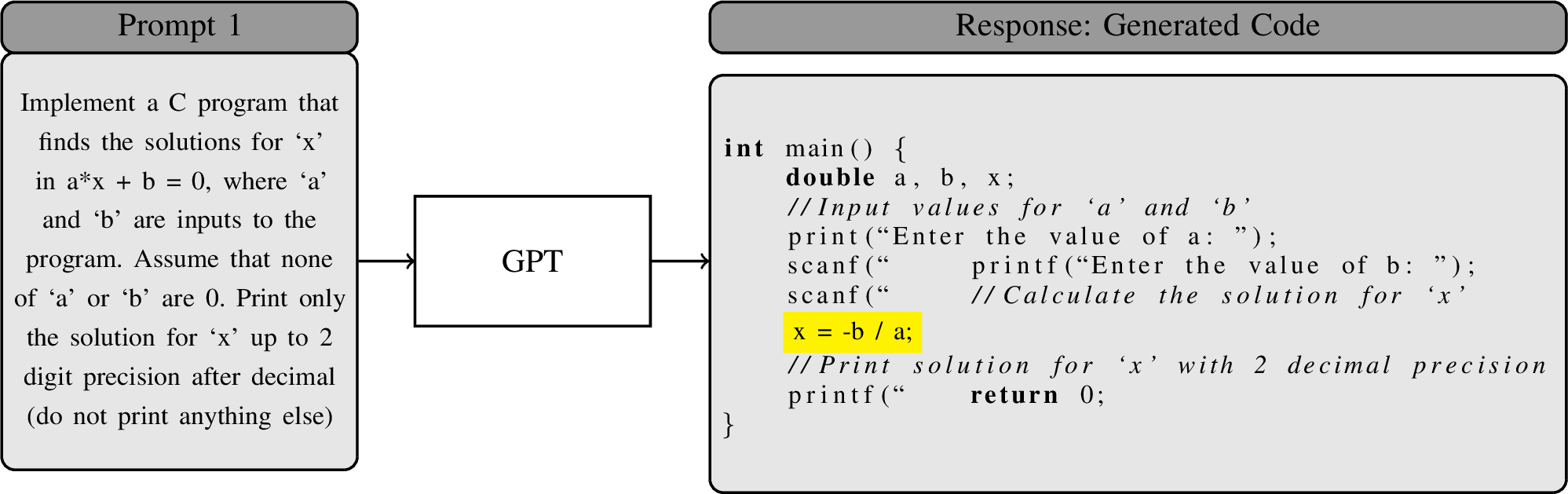
Figure 1: Prompt Example 1 and the generated code by the LLM-based code generator.
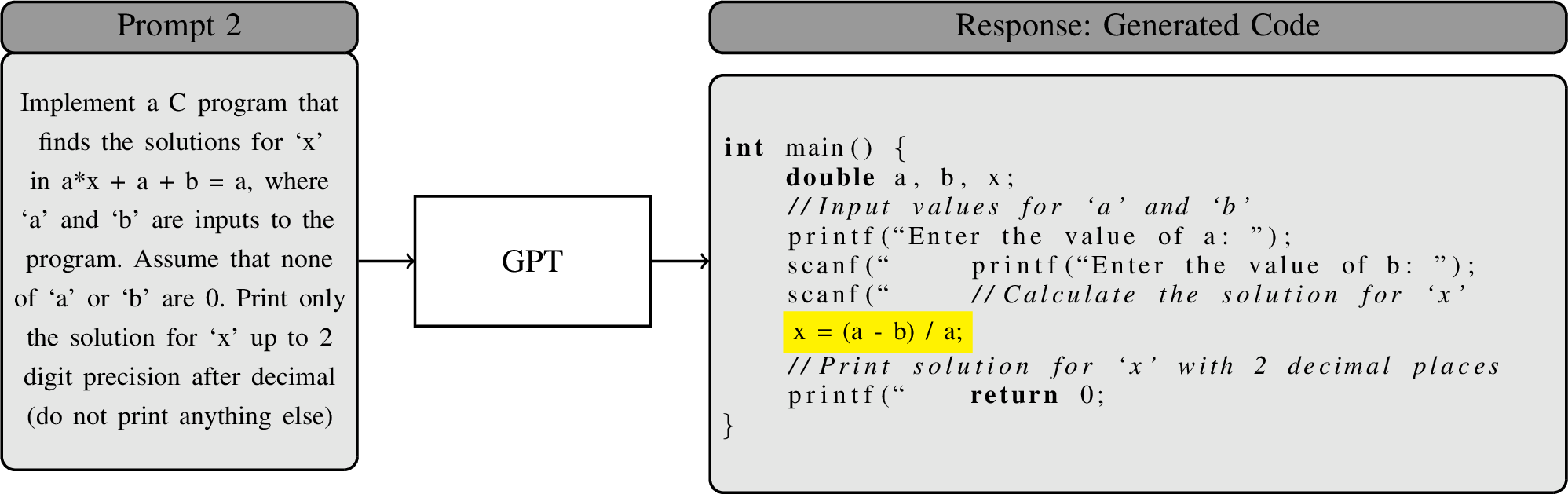
Figure 2: Prompt Example 2 and the code generated by the LLM-based code generator.
We start with a motivating example where we show a pair of semantically equivalent but syntactically different code generation prompts, and the output generated by the LLM-based code generator GPT-4 in response to these prompts. Figures 1 and 2 demonstrate two semantically equivalent prompts with syntactic differences and the code returned by the GPT-4 for these two prompts. Prompts 1 and 2 are given as two distinct queries to GPT-4 as shown in Figure 1 and Figure 2.
Both prompts contain the same English text with two syntactically different mathematical formulas. The mathematical formulas are \(a \times x + b = 0\) and \(a \times x + a + b = a\) which are both linear equations with coefficients \(a\) and \(b\). Even though they are syntactically different, they are semantically equivalent. This means that the solution for variable \(x\) remains the same in both formulas. Given the two prompts, we expect the LLM-based code generator to generate semantically equivalent code. However, it is evident from Figures 1 and 2 that the generated code are not semantically equivalent. The first code solves the values of \(x\) as \(-b/a\), whereas the second one solves it as \((a-b)/a\). In this case, it is easy to verify that only the first code yields the correct solution for \(x\). This example shows a case in which GPT-4 fails syntactic robustness even for a small syntactic change to the formula between the two queries.
To analyze the syntactic robustness of LLM-based code generation, our overall approach is to construct code generation prompts which only differ by the syntax of a mathematical formula present in the prompt (without modifying their sematics) and analyze the code generated in response to these prompts.
Similar to the prompts shown in Figures 1 and 2, we focus on linear, quadratic, trigonometric, and logarithmic equations for our analysis. We define mutation rules that syntactically modify a formula without changing its semantics, and check the syntactic robustness of LLM-based code generators using a set of mutants generated by applying mutations rules.
We use differential fuzzing to check the equivalence of generated code, and we use the results of differential fuzzing to assess the degree of syntactic robustness for an LLM-based code generator.
We propose a pre-processing step for prompt reduction in order to improve syntactic robustness. Pre-processing step syntactically modifies the formula in a prompt without changing its semantics. It uses reduction rules to simplify the formula by reducing its size. Our experimental evaluation shows that reducing the formula size is a good strategy for achieving high degree of syntactic robustness.
The rest of the paper is organized as follows. We provide a formal definition of syntactic robustness and related concepts in Section 3. Next, we detail our construction of code generation prompts in Section 4, explain our equation transformation procedure in Section 5, explain our pre-processing procedure in Section 6, and then explicate implementation details in Section 7. We then present our experimental evaluation in Section 8, discuss the related work in Section 9, and conclude our paper in Section 10.
3 Syntactic Robustness↩︎
In this section, we formalize the concept of syntactic robustnesss for LLM-based code generators. After defining LLM-based code generators and the type of code generation prompts we are focusing on, we define programs as functions, we define their equivalence, followed by our definition of syntactic robustness.
3.0.0.1 LLM-based Code Generators
We define an LLM-based code generator as follows:
Definition 1. An LLM-based code generator \(G\) takes a prompt \(P \in \cal P\) as input and generates code \(C \in \cal C\) denoted as: \(G: \cal P \rightarrow \cal C\), where \(\cal P\) is the set of prompts and \(\cal C\) is the set of programs.
In this paper, we focus on C code, i.e., \(\cal C\) denotes the set of C programs. Furthermore, we focus on prompts that contain both English text and mathematical formulas:
Definition 2. A prompt \(P \in \cal P\) consists of an English text \(T\) and a mathematical formula \(F\) denoted as a tuple \(P \langle T, F \rangle\).
When an LLM-based code generator generates code \(C\) for prompt \(P\langle T, F\rangle\), we denote it as: \(G (P\langle T, F\rangle) = C\).
3.0.0.2 Semantic Equivalence of Formulas
Two syntactically different formulas \(F_1\) and \(F_2\) can be semantically equivalent. We denote the semantic equivalence of two formulas \(F_1\) and \(F_2\) as: \[[\![ F_1 ]\!] \equiv [\![ F_2 ]\!]\] which means that all valuations that make formula \(F_1\) evaluate to true also make formula \(F_2\) evaluate to true and vice versa (i.e., the solution sets of \(F_1\) and \(F_2\) are the same).
For example, consider the two formulas \(F_1\) and \(F_2\): \[\begin{align} F_1&:& a \times x + b = 0 \\ F_2&:& a\times x + a + b = a \end{align}\] Note that although \(F_1\) and \(F_2\) are syntactically different formulas (i.e., \(F_1 \neq F_2\)) they are semantically equivalent: \([\![ F_1 ]\!] \equiv [\![ F_2 ]\!]\).
3.0.0.3 Programs as Functions
In this paper, we are focusing on programs that can be modeled as functions. For a given input, we assume that each execution of a program terminates and returns the same output. Formally:
Definition 3. A program \(C\) is a total function from the domain of inputs to the domain of outputs, \(C: I \rightarrow O\), where \(C(i) = o\) denotes that on input \(i \in I\), the output of \(C\) is \(o \in O\).
3.0.0.4 Program Equivalence
We define equivalence of programs based on their input-output behavior:
Definition 4. Given two programs \(C_1: I_1 \rightarrow O_1\) and \(C_2: I_2 \rightarrow O_2\) where \(I_1 = I_2\),
\(C_1\) and \(C_2\) are equivalent, denoted as \([\![ C_1 ]\!] \equiv [\![ C_2 ]\!]\), if and only if, \(\forall i \in I, C_1(i)= C_2(i)\).
\(C_1\) and \(C_2\) are non-equivalent, denoted as \([\![ C_1 ]\!] \not \equiv [\![ C_2 ]\!]\), if and only if, \(\exists i \in I, C_1(i) \neq C_2(i)\).
Note that different implementations of the same functionality are considered equivalent according to this definition as long as the input-output behavior is the same.
3.0.0.5 Syntactic Robustness
We can now define syntactic robustness for LLM-based code generators:
Definition 5. An LLM-based code generator \(G\) is syntactically robust, if and only if, given any two prompts \(P\langle T,F_1\rangle, P\langle T,F_2\rangle \in \cal P\) where \([\![ F_1 ]\!] \equiv [\![ F_2 ]\!]\), \([\![ G(P\langle T,F_1\rangle) ]\!] \equiv [\![ G(P\langle T,F_2\rangle) ]\!]\).
i.e., an LLM-based code generator is syntactically robust if it generates equivalent code for semantically equivalent but syntactically different prompts.
There are two issues with the above definition. First, note that, the above definition of syntactic robustness requires the LLM-based code generator to generate semantically equivalent programs for all semantically equivalent prompts. Even if the code generator generates semantically different code for only one syntactically different prompt while generating semantically equivalent code for all other prompts, it is not syntactically robust according to the above definition. So, one possibility is to extend the definition above to measure the syntactic robustness degree where Definition 5 corresponds to the highest degree of syntactic robustness.
Second, according to Definition 5, if an LLM-based code generator generates the same code for all prompts (semantically equivalent or not), it would be syntactically robust. i.e., an LLM-based code generator that for all prompts generates the same trivial code such as:
int main() {
printf("0\n");
return 0;
}would be syntactically robust. In order to address this problem, we introduce the concept of a reference code for each prompt as follows:
Definition 6. Given a prompt \(P \langle T, F \rangle\) we call \(R(P\langle T, F\rangle) = C^R_F\) the reference code for the prompt \(P \langle T, F \rangle\), where \(C^R_F\) is a correct implementation of the requirements specified in the prompt \(P \langle T, F \rangle\).
Note that \(C^R_F\) can be written manually or can be generated by a code generator and validated by other means (such as manual inspection, testing, or verification).
We now define syntactic robustness degree for an LLM-based code generator for a given prompt, its reference code, and its syntactic variations as follows:
Definition 7. Given an LLM-based code generator \(G\), a prompt \(P\langle T,F\rangle\), a reference code \(R(P\langle T, F\rangle) = C^R_F\) for prompt \(P\), and a set of formulas \({\cal F}_F\) containing syntactic variations of \(F\) where for each \(F' \in {\cal F}_F\), \([\![ F' ]\!] \equiv [\![ F ]\!]\), let \({\cal F}^{eq}_F \subseteq {\cal F}_F\) denote the set of formulas such that for each \(F' \in {\cal F}^{eq}_F\), \([\![ G(P\langle T,F'\rangle) ]\!] \equiv [\![ C^R_F ]\!]\). Then, the syntactic robustness degree of \(G\) with respect to \(P\) and \(\cal F_F\) is defined as: \[|{\cal F}^{eq}_F| / |{{\cal F}_F}|\] where \(|{\cal F}^{eq}_F|\) denotes the number of formulas in \({\cal F}^{eq}_F\) and \(|{\cal F}_F|\) denotes the number of formulas in \({\cal F}_F\).
We report the syntactic robustness degree as a percentage where 100% corresponds to the case where \({\cal F}^{eq}_F ={\cal F}_F\). Note that the syntactic robustness definition given in Definition 5 corresponds to syntactic robustness degree of 100% for all prompts and all semantically equivalent syntactic variations of prompts.
4 Code Generation Prompts for Equations↩︎
In order to investigate syntactic robustness of LLM-based code generators, we use code generation prompts based on a set of univariate equations. These prompts include an equation and ask for generation of code that takes coefficients of the equation as input and returns values of the variable that satisfy the equation as output, i.e., the generated code is required to solve the equation given a set of coefficients as input.
4.0.0.1 Equations
We use univariate polynomial, trigonometric and logarithmic equations. In particular, we have chosen the following equation categories:
Polynomial equations with degree 1 and 2
\(a \times x + b = 0\) (linear equation)
\(a \times x ^ 2 + b \times x + c = 0\) (quadratic equation)
Trigonometric equations
\(a \times \mathit{sin(x)} = b\)
\(a \times \mathit{cos(x)} =b\)
\(a \times \mathit{tan(x)} =b\)
Logarithmic equations with base 10 and e
\(a \times \mathit{log(x)} =b\)
\(a \times \mathit{ln(x)} =b\)
The context-free grammar shown in Figure 3 captures the formulas corresponding to univariate equations listed above and their variations, where \(F\) denotes the start symbol corresponding to the equation, \(E\) denotes expressions, \(U\) denotes unary functions, \(N\) denotes number literals, \(Q\) denotes coefficients, and \(V\) is the single variable.
None
Figure 3: Our context-free grammar for univariate polynomial, trigonometric and logarithmic equations.
4.0.0.2 Code Generation Prompts
Our prompts contain English text explaining the code generation task along with the mathematical formulas discussed above. Due to the mutations we apply to the mathematical formulas (which we discuss in the next section), the semantics of a formula can change if the values of the coefficients can be 0 (for example due to division by zero). Hence, we restrict the solution space to cases where coefficients are not 0 and we state this assumption in all of the prompts. Additionally, we provide specific instructions in the prompt on the input and output formats to make the prompt precise and avoid ambiguity in the English text containing code generation instructions. The following are the prompts we have used to investigate syntactic robustness based on univariate equations discussed above, where the part of the prompt that states the equation is replaced with the corresponding equation or one of its syntactic variants (generated by the mutations we discuss in the next section):
Prompt 1 “Implement a C program that finds the solutions for ‘x’ in linear equation, where ‘a’ and ‘b’ are inputs to the program. Assume that none of ‘a’ or ‘b’ are 0. Print only the solution for ‘x’ up to 2 digit precision after decimal (do not print anything else).”
Prompt 2 “Implement a C program that finds the solutions for ‘x’ in quadratic equation, where ‘a’, ‘b’ and ‘c’ are inputs to the program. Assume that none of ‘a’, ‘b’, or ‘c’ are 0. Print only the solution for ‘x’ up to 2 digit precision after decimal (do not print anything else). Print the solutions in comma separated form. If there are no real solutions then print ‘No real roots’.”
Prompt 3 “Implement a C program that finds the solutions for ‘x’ in trigonometric equation, where ‘a’ and ‘b’ are inputs to the program. Assume that none of ‘a’ or ‘b’ are 0. Print only one of the solutions for ‘x’ in radian format up to 6 digit precision after decimal (do not print anything else).”
Prompt 4 “Implement a C program that finds the solutions for ‘x’ in logarithmic equation, in base 10 (not base e), where ‘a’ and ‘b’ are inputs to the program. Assume that none of ‘a’ or ‘b’ are 0. Print only the solution for ‘x’ up to 2 digit precision after decimal(do not print anything else).”
Prompt 5 “Implement a C program that finds the solutions for ‘x’ in logarithmic equation, in base e (not base 10), where ‘a’ and ‘b’ are inputs to the program. Assume that none of ‘a’ or ‘b’ are 0. Print only the solution for ‘x’ up to 2 digit precision after decimal(do not print anything else).”
4.0.0.3 Reference Code
For each type of equation \(F\), we manually implemented a reference code \(C^R_F = R(P\langle T, F\rangle)\) making sure that \(C^R_F\) correctly implements the requirements specified in the prompt \(P\langle T, F\rangle\). Given the reference code \(C^R_F\) and a set of formulas \({\cal F}_F\) that are syntactically different but semantically equivalent to \(F\), syntactic robustness checking corresponds to checking for each \(F' \in {\cal F}_F\) if \([\![ G(P\langle T,F'\rangle) ]\!] \equiv [\![ C^R_F ]\!]\). In the next section we discuss how we generate the set of formulas \({\cal F}_F\) that are syntactic variations of a given equation \(F\).
5 Syntactic Transformations and Mutations for Equations↩︎

Figure 4: Mutation rules for equations.
We start this section by defining syntactic transformations and the sizes of formulas before we introduce mutations.
Definition 8. A syntactic transformation \(ST\) is a function that maps a formula to another formula that is semantically equivalent, i.e., \(ST: {\cal F} \rightarrow {\cal F}\) such that for any formula \(F \in {\cal F}\), \([\![ F ]\!] \equiv [\![ ST(F) ]\!]\), where \({\cal F}\) denotes the set of formulas.
Given a formula \(F\) its size, denoted as \(|F|\), is the number of terminal symbols in the formula according to the context free grammar shown in Figure 3. We define a mutation as a syntactic transformation that does not decrease, but can increase, the size of the formula:
Definition 9. A mutation \(M\) is a syntactic transformation where for each formula \(F \in {\cal F}\), \(|M(F)| \geq |F|\).
I.e., a mutation modifies the syntax of the formula without changing its semantics, while the size of the modified formula is either the same or larger than the size of the original formula.
We can apply mutation operations multiple times to the same formula \(M(F), M(M(F)), M(M(M(F))), \ldots\) to create multiple mutants of the formula \(F\). We use \(M^n(F)\) to denote the application of \(n\) mutations to formula \(F\) and we use \(M^+(F)\) to denote the application of one or mutations to formula \(F\).
We define five types of mutations for equations as described by the rules shown in Figure 4. These mutations are reasonably straightforward—M1 switches the sides of an equation, and M2–5 change each side of the equation by applying a constant value \(Q\) from the set of constants already in the equation to each side using the same mathematical operation. As the equations we use are joined with equality, and we assert that any constant in \(Q\) cannot be zero, all of these mutations must produce syntactically equivalent formulas. The specific constant chosen for \(Q\) in each mutation must already be present in the formula—we do not introduce new constants during these mutations.
Given a formula \(F\), we generate the set of syntactic mutations of \(F\), called \({\cal F}_F\) (as described in Definition 7) by repeatedly applying mutations defined in Figure 4 to \(F\). I.e., each \(F' \in {\cal F}_F\) is \(F' =M^+(F)\) for some sequence of mutations, and by definition of mutations, \([\![ F' ]\!] \equiv [\![ F ]\!]\) as required for \({\cal F}_F\) in Definition 7.
Our specification that each applied mutation must not decrease the size of the formula may fail if two mutations cancel each other out. To prevent this scenario, when we apply mutations as a sequence, we make sure that none of the mutations cancel each other out.
It is reasonable to assume that a formula \(F'\) which is the result of applying multiple syntactic transformations to an original formula \(F\) will appear more syntactically different with more transformations. In order to capture this notion, we define the syntactic distance of a mutated formula as follows:
Definition 10. Given a formula \(F\) and its syntactic mutant \(F'\), the syntactic distance of \(F\) and \(F'\) is \(n\) when \(F' = M^n(F)\).
I.e., the syntactic distance of \(F\) and its mutant \(F'\) is the number of mutations needed to mutate \(F\) to \(F'\).
We use syntactic distance in our experimental evaluation of the impact of the mutations on syntactic robustness as discussed in Section 8. As the syntactic distance of the original formula and the mutated formula increases, it is likely to become more difficult for the LLM-based code generator to achieve syntactic robustness. Our experimental evaluation presented in Section 8 demonstrates that this is indeed the case. In the next section we propose an approach to remedy this problem.
6 Prompt Pre-processing with Formula Reduction for Improving Syntactic Robustness↩︎

Figure 5: Reduction rules for equations.

Figure 6: Prompt pre-processing with formula reduction in order to improve syntactic robustness.
Our experimental evaluation (Section 8) indicates that the syntactic distance and syntactic robustness degree are inversely related, i.e., as the syntactic distance increases, syntactic robustness degree decreases. Note that the mutations increase the sizes of the formulas (Definition 9) and, therefore, our experiments indicate that as the sizes of the formulas increase the degree of syntactic robustness decreases.
These observations suggest an approach for improving the syntactic robustness of LLM-based code generation using a pre-processing step. In contrast to mutations, we can consider syntactic transformations that reduce the size of a given formula with the assumption that shorter formulas are simpler and prompts that contain shorter formulas are more likely to be processed correctly by an LLM-based code generator. We call such syntactic transformations reductions.
6.0.0.1 Reductions
We formally define reductions as a type of syntactic transformations as follows:
Definition 11. A reduction \(M\) is a syntactic transformation where for each formula \(F \in {\cal F}\), \(|M(F)| \leq |F|\).
I.e., a reduction modifies the syntax of the formula without changing its semantics, while the size of the modified formula is either the same or less than the size of the original formula.
We define five types of reductions for equations as described by the rules shown in Figure 5. Reduction rule R1 positions all nonzero elements of the equation on one side of the equality operator.
Reductions R2 and R3 show a series of possible applications for removing redundant additions and subtractions—specifically, the two final applications show removal of these redundant applications when a different additive or subtractive term intercedes the redundant application.
Reductions R4 and R5 show a series of possible applications for removing redundant divisions and multiplications—this is to show that this removal may not necessarily be from one singular \(E\) comprising the full side of the formula but may also be from each individual additive or subtractive term on that side.
It is worth noting that the reduction rules described in Figure 5 are opposite of the mutation rules described in Figure 4. As opposed to increasing the size of the formula, they decrease the size of the formula with the goal of simplifying it.
6.0.0.2 Prompt Pre-processing
Figure 6 shows the workflow for our pre-processing step based on prompt-reduction. Instead of feeding the prompts with mathematical formulas as-is, we introduce a pre-processing step and generate a reduced/simplified version of that formula by repeatedly appliying the reductions presented in Figure 5. Then the reduced prompts with the same English text and reduced mathematical formulas are fed to the LLM-based code generator to generate the target code.
All of our pre-processing begins with the application of a specialized reduction rule R1 as described in Figure 5, to position all nonzero elements of the equation on one side of the equality operator. Following this reduction, we apply rules R2–5 described in Figure 5 in a loop until no further changes can be made to the equation.
7 Implementation↩︎
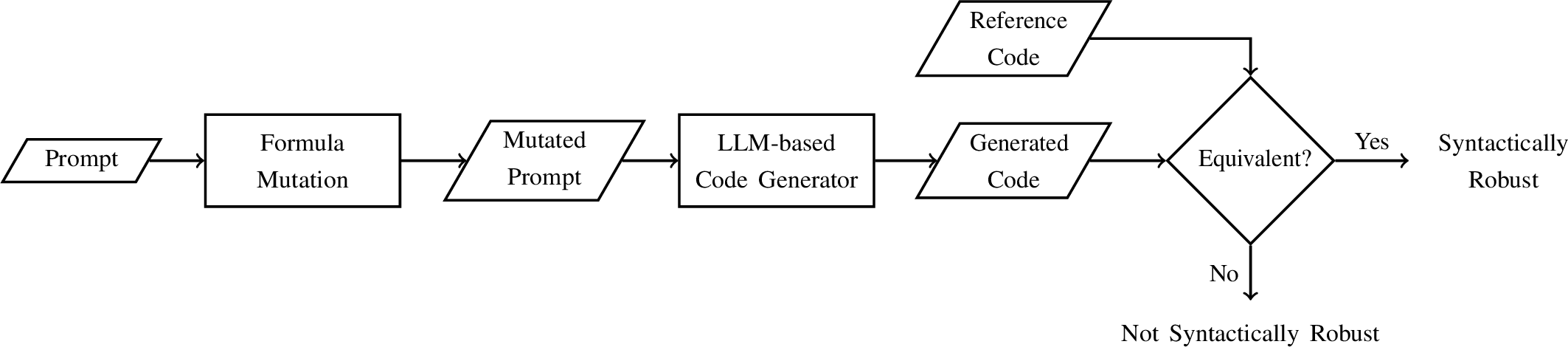
Figure 7: Syntactic robustness checking (this workflow is applied in a loop for multiple mutations).
Our syntactic robustness checking for LLM-based code generators contains several steps, as shown in Figure 7. A prompt with a query to generate code is passed on to the LLM-based code generator, providing us with the generated code as a response. The generated code is then compared with our reference code to evaluate its syntactic robustness. The implementation detail in each step is described below:
Mutated equation generation: The prompt is generated with English text and a mathematical formula, which is an equation. To measure the impact of the syntactic distances on the generated code, we have generated 20 variations per distance between 1 and 5. Even though we get 20 variations each for distances 2 to 5, the number of variations generated at distance 1 is less than 20, mainly due to the limited number of mutation rules and the constraint on not allowing the decrement of the size of the equation. We have generated a total of 627 variations for seven types of equations.
Post-processing of the GPT responses: The GPT responses contain English text explaining the code and the generated code when asked for a code. Our implementation takes the generated response from the GPT, eliminates the redundant texts, and finally converts it to a C file. The C files are then compiled into binaries using GCC [7], which is also automated in our pipeline. Any C code with syntactic errors will not be compiled into binaries due to the presence of errors and will be considered non-equivalent with respect to our reference code.
Non-determinism of GPTs: We are aware of the fact that GPTs are non-deterministic. To reduce the non-determinism, we used temperature and seed values of 0. We have also tested different setups with temperature, top_p, and seed values and chose the one that provides the most deterministic results. Moreover, we have asked GPT to provide code five times for the same prompt to analyze the impact of non-determinism. In our experiments, we queried both the GPTs with a total of 3135 queries (\(627\times5\)). Even though there are 627 equation variations, the final syntactic robustness degree is calculated by the number of equivalent programs out of these 3135 generated programs.
Code equivalence: We have implemented reference solutions for each of the chosen equations. We check the equivalence with the reference solutions using differential testing for each generated code by randomly generating 1000 input cases and comparing the outputs from the generated code with our reference solution. Even though specified in the prompt not to print anything except for the solution, the outputs can be in different formats like printing “solution is or x=”. So, we have also post-processed the outputs from the generated programs for equivalence analysis. Moreover, we have asked the GPT to provide the output in a specific format with 6-digit or 2-digit precision, not printing anything other than the result and printing only the real solutions. We only asked for 6-digit precision for trigonometric equations as the solutions of those equations can be very small.
To compare the float outputs from the generated programs and reference solutions, we considered them correct if they are within a defined epsilon value. For 2-digit precision, epsilon is 0.02; for 6-digit precision, it is 0.000002. We added the epsilon to reduce the impact of rounding errors for floating point outputs from the generated codes. This relaxes our Definition 4 of equivalence of two programs. Moreover, there are cases where, for example, when a logarithmic equation has variables multiple times, the rounding impact gets amplified, and it might provide non-equivalence even though the codes are equivalent.
For example, equation \(a \times log(x) = b\) gets mutated to \(b / a^{2} = \mathit{log}(x)/a\) which is calculated in the code as \(x = \mathit{pow}(10, b/ (a \times a) \times a)\) which is equivalent to \(x = \mathit{pow}(10, b/a)\) (non-equivalent case for inputs \(a=27, b=427\)). So, in the equivalent analysis of the codes where we get equivalent outputs for \(\geq\)90% of the cases, we manually check those programs to determine whether the reason is due to rounding impact or something else.
The inputs to the programs are the independent variables of the equations, which are randomly chosen between -1000 and 1000 for differential testing. For testing the trigonometric equations sine and cosine, we have only considered input parameters such that the value of \(\mathit{sin(x)}\), \(\mathit{cos(x)}\) remains within -1 and 1.
Syntactic robustness degree: For two input variables, the input domain is \(2^{32} \times 2^{32}\) for differential testing and for 3 variables it would be \(2^{32} \times 2^{32} \times 2^{32}\) considering the inputs are in 32-bit representation. As we are unable to test that many inputs (which would be required to verify full equivalence), we test the program equivalence with a subset of the input domain (1000 inputs). This, by necessity, means we calculate the syntactic robustness degree with respect to a subset of the input domain. We used Python to implement the full pipeline and Python’s sympy [8] module to implement mutation and reduction rules. The working pipeline is available at Link.
8 Experimental Evaluation↩︎
In our experimental evaluation, we address four key research questions:
RQ1: Does GPT-based code generation have syntactic robustness?
RQ2: Does a larger number of mutations to an equation yield lower syntactic robustness?
RQ3: Do different types of mutations affect syntactic robustness differently?
RQ4: Does prompt pre-processing with formula reduction improve the syntactic robustness of code generation?
8.1 Experimental Setup↩︎
We experimented with GPT-3.5-turbo and GPT-4 as our LLM-code generator and used APIs to get the generated codes. We ran our experiments on a machine with a 13th Gen Intel Core i9-13900K CPU at 3.00GHz and 192 GB of RAM running Ubuntu 22.04.4 LTS. We have used the same equation variations to test the GPT-3.5 and GPT-4.
8.2 Experimental Results↩︎
In this section, we present the results of our experiments and discuss the four research questions we are addressing.
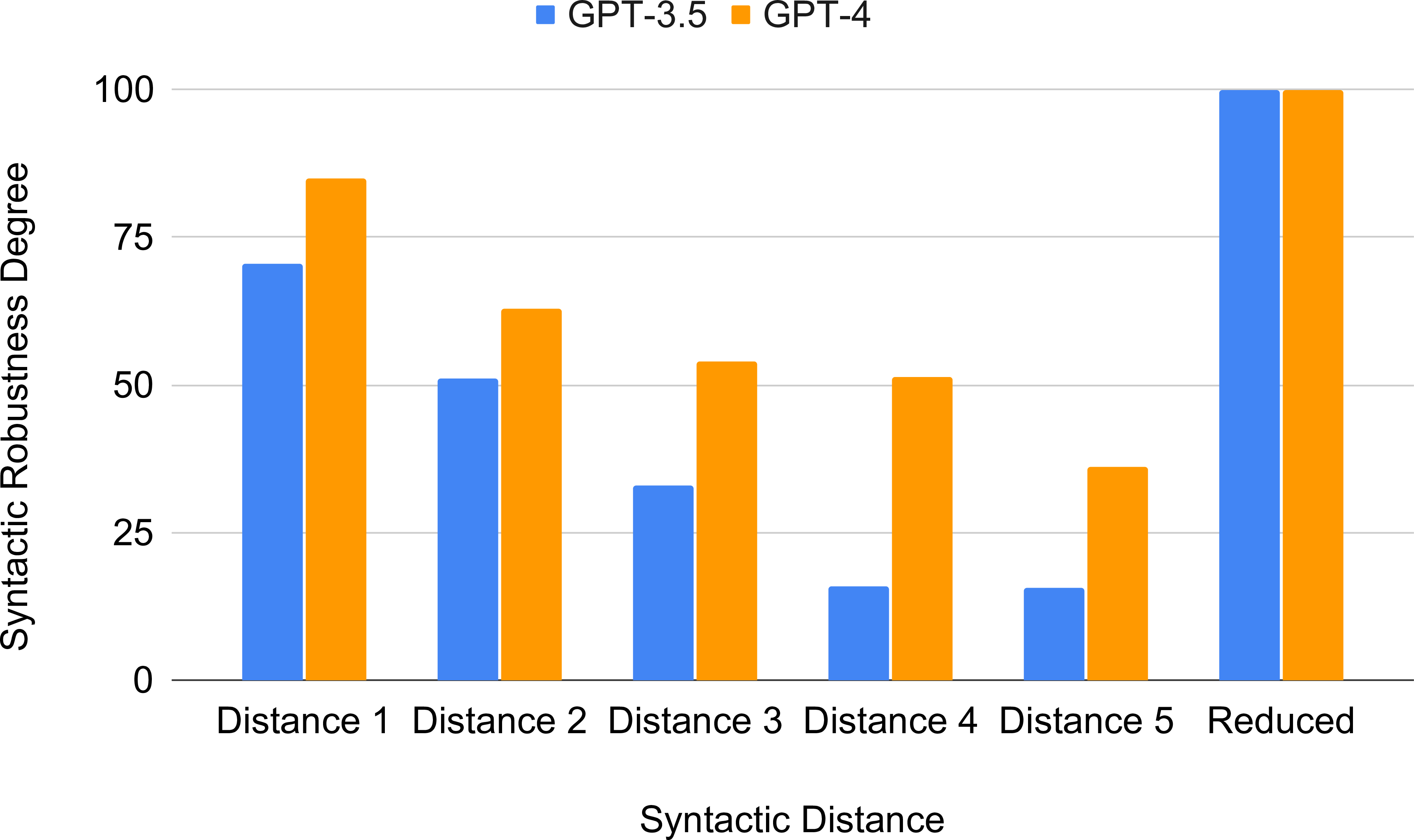
Figure 8: Syntactic Robustness Degree Vs. Distance
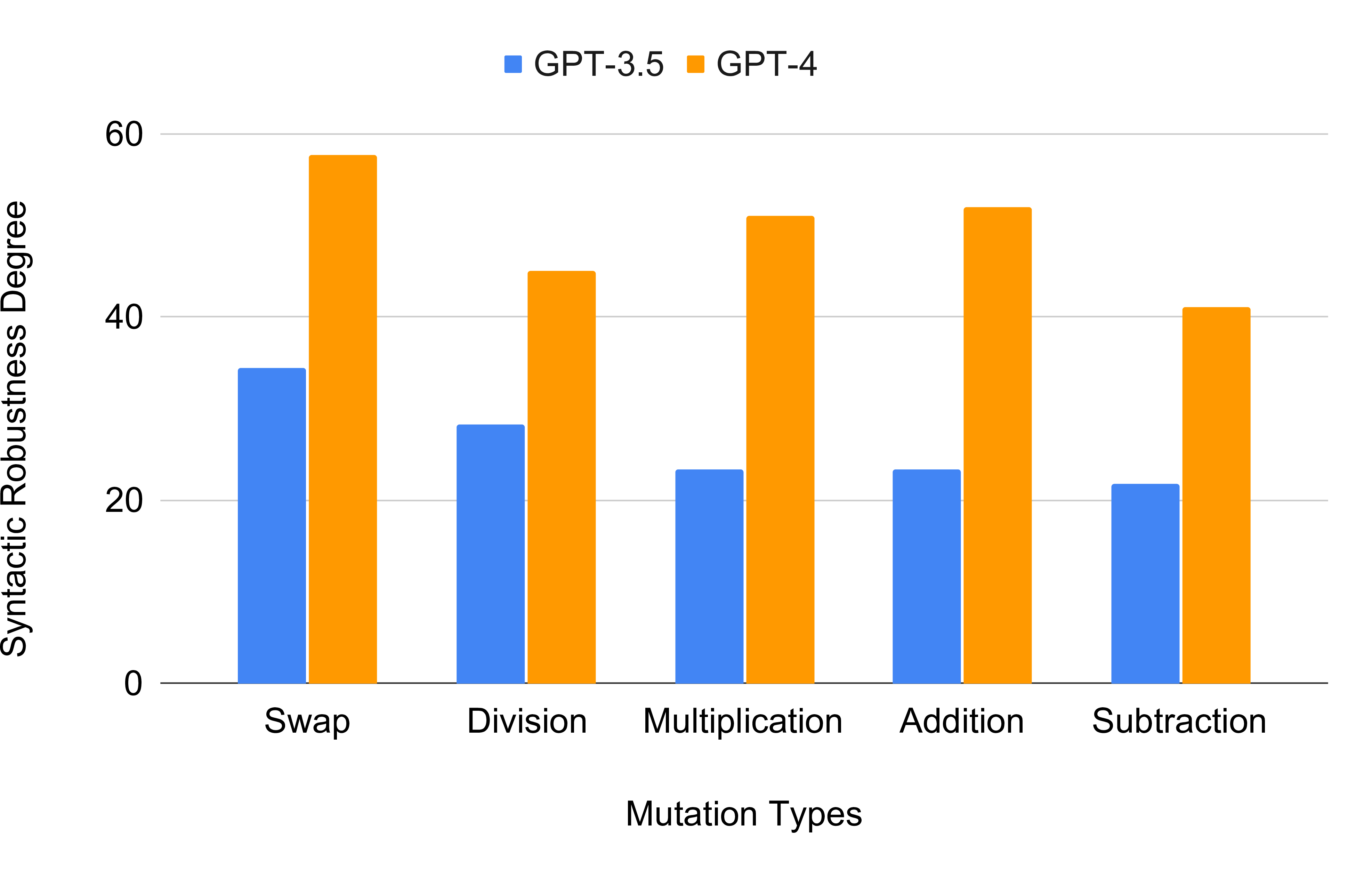
Figure 9: Syntactic Robustness Degree Vs. Mutation types
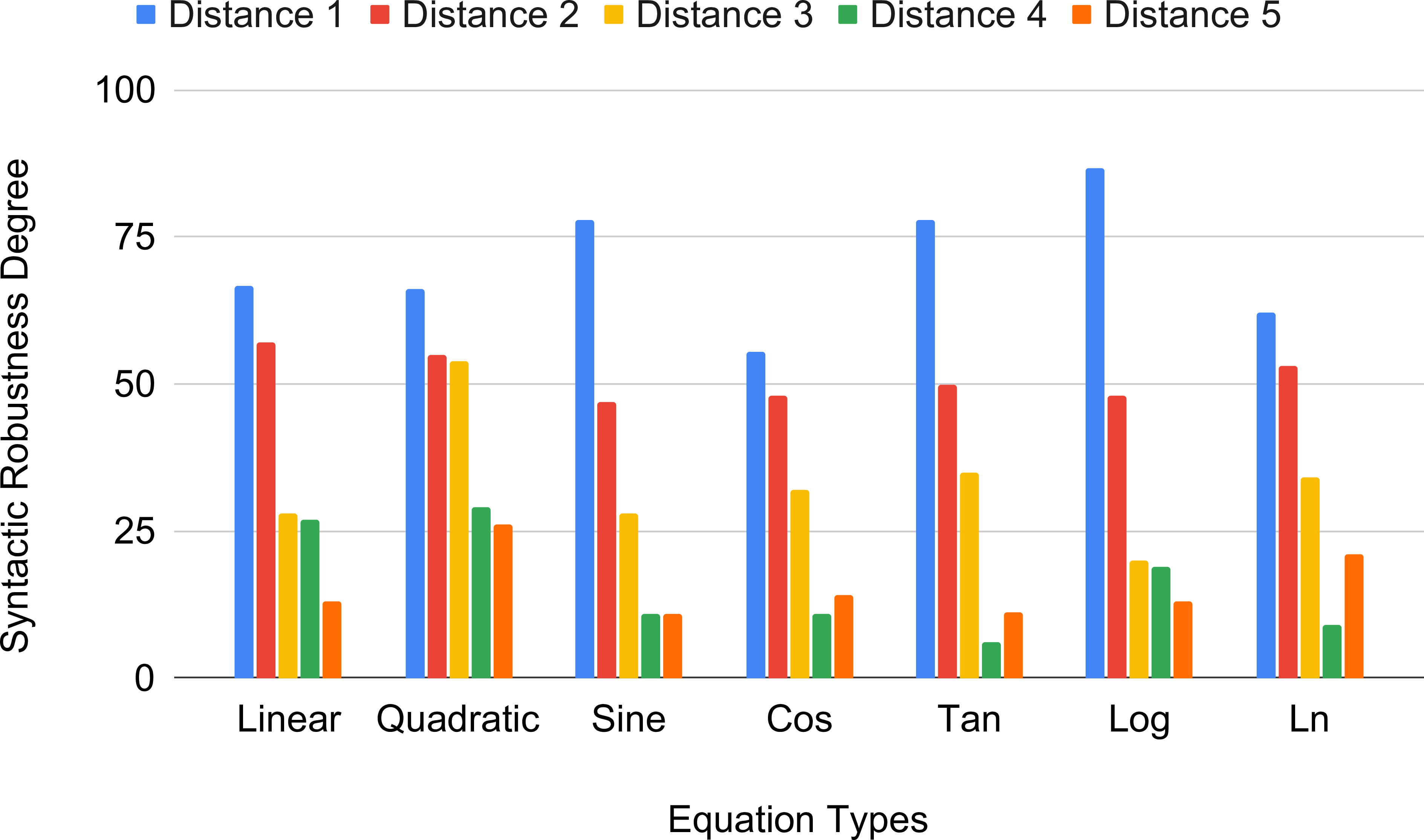
Figure 10: GPT-3.5: Syntactic robustness degree for equations
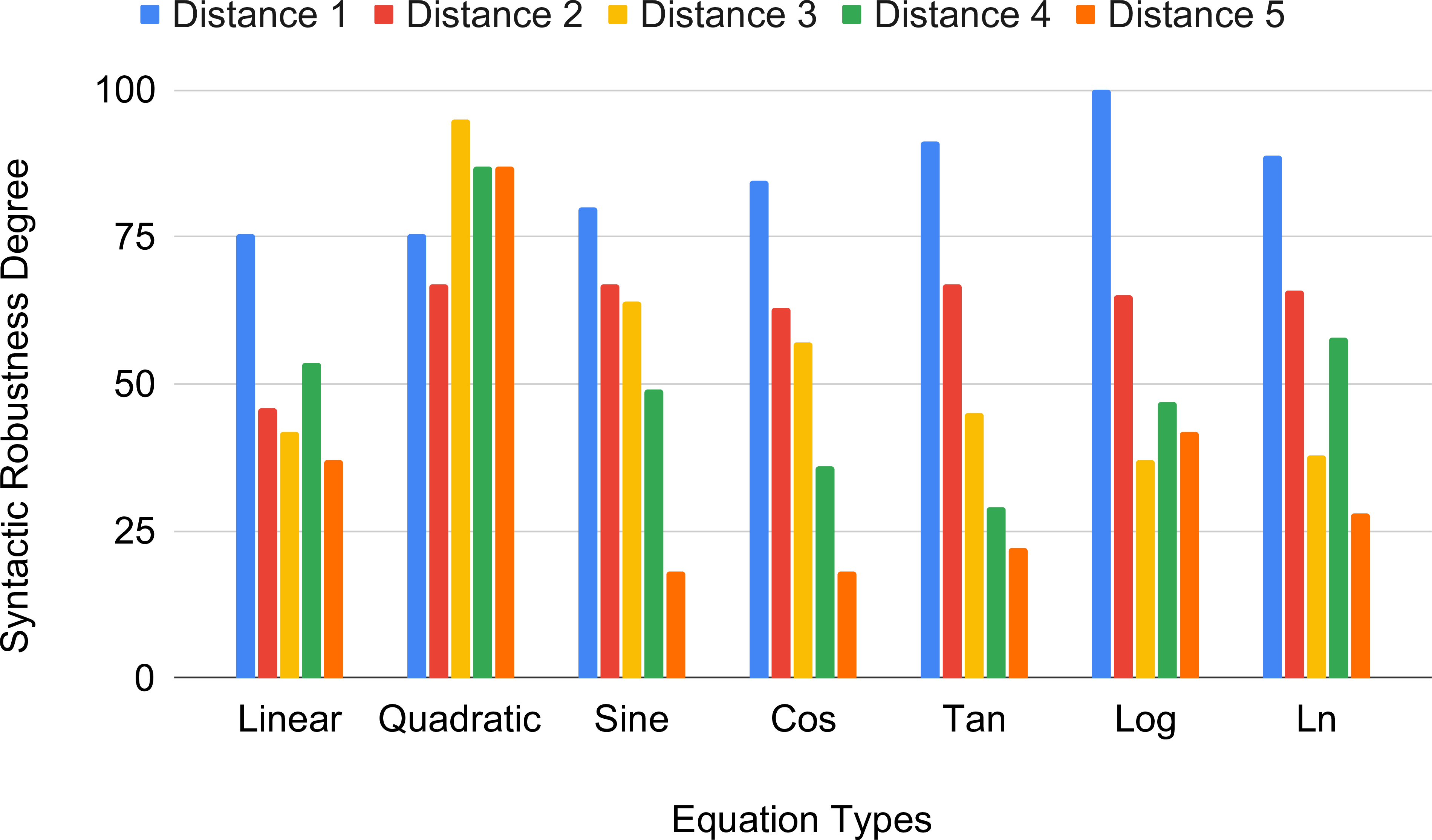
Figure 11: GPT-4: Syntactic robustness degree for equations
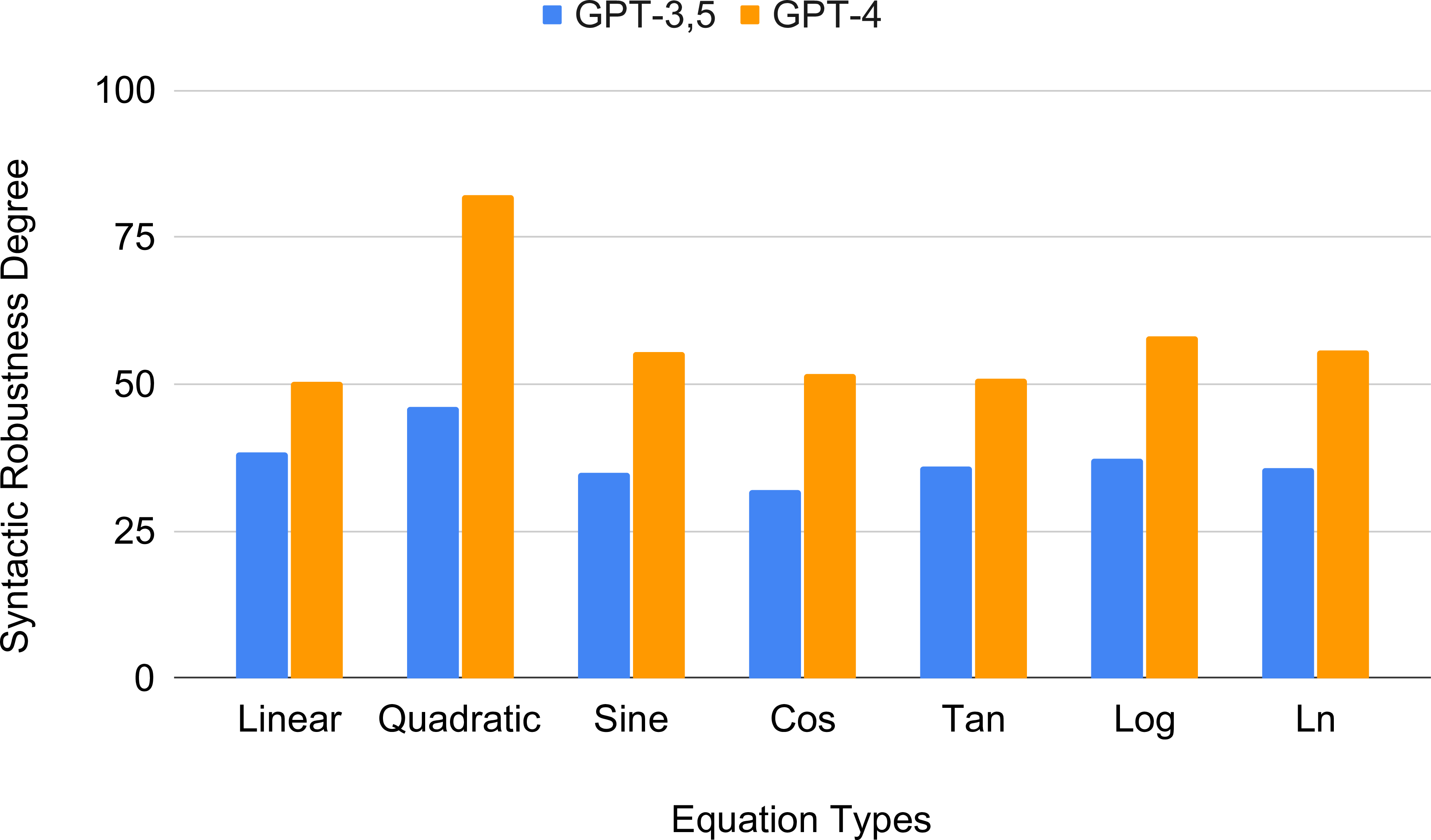
Figure 12: Syntactic Robustness Degree Vs. Equation types
RQ1: Does GPT-based code generation have syntactic robustness? From the results showcased in Figure 10 and 11, it is evident that the syntactic robustness degree is reduced for both of the GPTs with the increased syntactic distance. Figure 8 shows the percentage syntactic robustness degrees for GPT-3.5 and GPT-4 for different syntactic distances by averaging the syntactic robustness degrees for all equations; importantly, all of these are less than 100%. From aggregate results, it is noticeable that for all the cases from syntactic distance 1 to 5, GPT-4 has a higher syntactic robustness degree than GPT-3.5, which is expected as we know GPT-4 is a larger model with more extensive training [9]. Even though GPT-4 has performed 1.55 times better than GPT-3.5, both of them have low syntactic robustness for mutated prompts. Note that syntactic distance 1 has only one mutation applied to our equations, and still, both GPT-3.5 and GPT-4 have failed to reach the maximum syntactic robustness degree. So, we can conclude that GPT-3.5 and GPT-4 do not have syntactic robustness.
RQ2: Does a larger number of mutations to an equation yield lower syntactic robustness? Figure 8 shows the average syntactic robustness degree for each syntactic distance for GPT-3.5 and GPT-4. The average syntactic robustness degrees for syntactic distances 1, 2, 3, 4, and 5 are 85.05%, 63%, 54%, 51.37%, and 36% respectively, in GPT-4. Similarly, the syntactic robustness degrees are 70.40%, 51%, 33%, 16%, and 15.59% on average for distances 1 to 5 in GPT-3.5. Observe that for both GPT-3.5 and GPT-4, the syntactic robustness degree decreases with the increase of syntactic distance following a negative correlation between them, i.e., more mutations to an equation create more confusion for the GPTs.
Figures 10 and 11 show the syntactic robustness degree and its relationship with syntactic distances for our seven equation types in GPT-3.5 and GPT-4, respectively. It is evident from these figures that in almost all cases, the syntactic distance of 1 (only a single mutation to the equation) is the least confusing one for the GPTs achieving the highest syntactic robustness degree. However, only the quadratic equation in GPT-4 in Figure 11 does not exhibit this pattern of negative correlation between the syntactic robustness degree and the syntactic distance and yields the highest syntactic robustness degree at a syntactic distance of 3.
We have further investigated cases where GPTs provide incorrect results with lower syntactic distances. For example, with syntactic distance 1, one of our mutated quadratic equations becomes \(a \times x^{2} +b \times x = -c\), and when generating the code, GPT-4 calculates the discriminant as \(b^{2} - 4 \times a \times (-c)\) instead of \(b^{2} - 4 \times a \times c\). Surprisingly, for higher syntactic distances, it can generate the correct code without making such incorrect interpretations. Even though the quadratic equation has the noisiest relationship between the syntactic robustness degree and the syntactic distances, especially in GPT-4, it is interesting that the quadratic equation achieves the maximum syntactic robustness degree with 82.28% in GPT-4 and 46.33% in GPT-3.5 (see Figure 12). The rest of the equation types have almost similar syntactic robustness degrees for each of GPT-3.5 and GPT-4. Although the results in Figure 10 and 11 show a few deviations from the pattern of negative correlation between syntactic robustness degree and syntactic distance per equation as different mutations may have different levels of impact, we can conclude from our aggregated result in Figure 8 that more mutations yield lower syntactic robustness.
RQ3: Do different types of mutations affect syntactic robustness differently? We have experimented with 5 different types of mutation rules for generating our mutated prompts. Figure 9 shows the impact of mutation types in the syntactic robustness degrees for GPT-3.5 and GPT-4. Swapping sides creates the least confusion for both GPTs and thus have the highest syntactic robustness degree with 34.37% and 57.77% in GPT-3.5 and GPT-4, respectively. On the other hand, subtraction has the lowest syntactic robustness degree in both, with 21.82% and 41.21% each. Division as a mutation confuses GPT-4 more than addition and multiplication. On the other hand, addition and multiplication have more impact than division in decreasing GPT-3.5’s robustness. The syntactic robustness with respect to multiplication and addition is almost similar, with 23.41% and 23.4% in GPT-3.5 and 51.06% and 51.99% in GPT-4. Overall, GPT-4 is less impacted by the applied mutations than GPT-3.5, but the individual mutations show a similar impact.
RQ4: Does prompt pre-processing with formula reduction improve the syntactic robustness of code generation? We have applied our reduction rules before asking the GPT-code generator for all the mutated variations generated from our seven equations. The last column of Figure 8 shows that the reduced form generated by our approach has successfully increased the syntactic robustness to 100%. For example, the reduced forms generated from all the mutated linear equations are in the forms of \(a \times x +b =0\) and \(-a \times x -b =0\). That means the reduced forms are actually the simplified forms of the mutated equations. Our observation is that an increment in the syntactic distance, which implies increasing the number of operators or having expressions on both sides of the equations, creates confusion for the GPT-code generator. A simple change in the equation can also produce semantically non-equivalent codes as shown in the example Figures 1, 2 and also in the example of RQ2. However, our reduction rules have successfully pre-processed the prompts, and our experimental results confirm that with our pre-processing step to reduce the equation to a simplified form, 100% syntactic robustness can be achieved.
8.3 Threats to Validity↩︎
We discuss possible internal and external threats to validity and the efforts we have made to mitigate them.
8.3.0.1 Internal
There are a few possible internal threats to validity within our experimental design. First, there is the possibility that the GPT API may be learning from prior requests we send and finding the patterns in our repeated prompts, which could skew the accuracy of results. We believe this is not the case, as we have switched APIs during these experiments multiple times and found no observable difference between code returned from a previously-used API and code returned from a fresh one. Second, we note that differential testing cannot prove equivalence and along the same vein the epsilon value we use in testing may not be perfect for each formula’s situation, both of which may artificially cause generated code to be marked as equivalent when it is not. This is a possible risk of any testing-based evaluation procedure, and we work to mitigate it by choosing a high number of samples in our differential testing (1000 per generated code) and a low epsilon value, but it is necessary to acknowledge for any cases where testing is involved that a lack of nonequivalent/failing tests is not a guarantee of correctness.
8.3.0.2 External
We analyze a small set of equations with a limited number of possible mutations, which we recognize may not be representative of all possible equations and mutations given to LLMs for code generation. We recognize this possibility but believe that our findings show promise for extending to the larger domain of all possible formulas and syntactically equivalent representations of those formulas.
9 Related Work↩︎
There have been many significant prior works in the domain of code generation by LLMs [10]–[12]. Authors in [10] released an evaluation set named HumanEval to obtain functional correctness of the generated program. Authors in [11], found components to obtain reliable code generation performance. The authors of [12] released Codegen that can perform program synthesis. There have also been many works in the recent past that perform studies on code generation abilities of these LLMs [13]–[20]. The authors of [13] explore the importance of prompts in the code generation capabilities of ChatGPT by using chain-of-thought strategy. The authors of [14] conducted an empirical study on the non-determinism of the codes generated from the ChatGPT. The authors of [16] performed a systematic evaluation of various code generation models. Paper [20] has worked on developing a framework to evaluate the performance of code generation from LLMs in a systematic manner. However, none of these studies focus on the syntactic robustness of LLM-based code generation.
Some works have also focused on improving the code generation with the help of prompt engineering [18], [21]–[27]. Our work can be considered as related to prompt engineering. However, we only modify the mathematical formula part of the prompt; the rest of the prompt remains static. The following works have performed scientific evaluation of LLMs for code generation [28]–[31]. Most of these works deal with the correctness of GPT and try to improve upon its correctness. Our definition subsumes correctness and expects a semantically equivalent response.
There have been work done on robustness evaluation of LLMs for code generation specificially [32], [33]. Authors of [32] perform a robustness study on copilot. However, they evaluate the robustness by asking the LLM with the original prompt to generate the code. Based on the generated code, Coco adds the program features such as loop as an instruction in the prompt. This should not change the second response as the requirement was already satisfied. Notice that this robustness definition is widely different from syntactic robustness defined in this paper. Paper [33] is also an empirical study that explores the robustness of the code with different semantically equivalent natural language descriptors. While they concentrated on mutating English texts, which often contain ambiguity, we emphasized mathematical formulas. Moreover, we have also proposed an approach to transform them into simplified forms to improve syntactic robustness.
As we briefly mentioned in Section 1, robustness has been studied in-depth in the realm of neural networks used for classification or numerical output tasks. These approaches include symbolic reasoning [34]–[39], abstraction [4], [40]–[42], and testing/fuzzing [43], [44]. The techniques available for these tasks, however, do not always translate easily to the domain of generative AI as the methods for modifying queries, as well as the assessment of whether or not a given result is correct, need adjustment. In addition, analysis of published generative AI tools must necessarily be black-box, which limits the techniques available for analysis. Moreover, the techniques used in our paper have similarities to a known testing technique known as Metamorphic testing [45]. Metapmorphic testing is a property based technique that uses known equality of specific output values from input relations. Metamorphic testing has been applied to LLMs [46], [47] in a different manner.
10 Conclusion↩︎
Use of LLM-based code generation is increasing. In this paper we demonstrated that GPT-4 and GPT-3.5 are unable to correctly generate code for prompts containing mathematical formulas, if simple semantic preserving mutations are applied to the formulas. We formalized this concept as syntactic robustness. We experimented with seven different equations in our prompts and asked GPTs for codes to generate solutions for those equations. We applied five mutation rules to mutate the mathematical equations and analyzed the syntactic robustness of GPTs with them. To improve syntactic robustness, we defined a set of reductions that transform the formulas to a simplified form and used these reductions as a pre-processing step. Our experimental results indicate that syntactic robustness can be significantly improved using our approach.
References↩︎
This material is based on research supported by National Science Foundation, Award #2124039, National Science Foundation, Award #2008660, National Science Foundation, Award #1901098.↩︎