Graphs without a \(3\)-connected subgraph are \(4\)-colourable
February 09, 2024
Abstract
In 1972, Mader showed that every graph without a \(3\)-connected subgraph is \(4\)-degenerate and thus \(5\)-colourable. We show that the number \(5\) of colours can be replaced by \(4\), which is best possible.
1 Introduction↩︎
Throughout the paper all graphs are finite and simple, and we only use standard notions and notation. We recall that a graph is \(k\)-connected if it has at least \(k+1\) vertices and no vertex cutset with at most \(k-1\) vertices. In 1972, Mader [1] proved the following theorem.
Theorem 1. For every integer \(k\geq 1\), every graph with average degree at least \(4k\) contains a \((k + 1)\)-connected subgraph.
Focusing on the case \(k = 2\) of 1, we call a graph fragile if it has no 3-connected subgraph. From 1, every non-null fragile graph has a vertex of degree at most 7. By restricting the proof of Mader to the case \(k=2\), it is easy to show that all fragile graphs \(G\) on at least four vertices satisfy \(|E(G)|\leq 2.5|V(G)| -5\) (we supply the proof in Section 3 for the sake of completeness). So the average degree of \(G\) is smaller than \(5\). Thus every fragile graph contains a vertex of degree at most 4, and this is best possible as shown by the graph in Figure [f:4]. Every fragile graph is therefore 5-colourable.
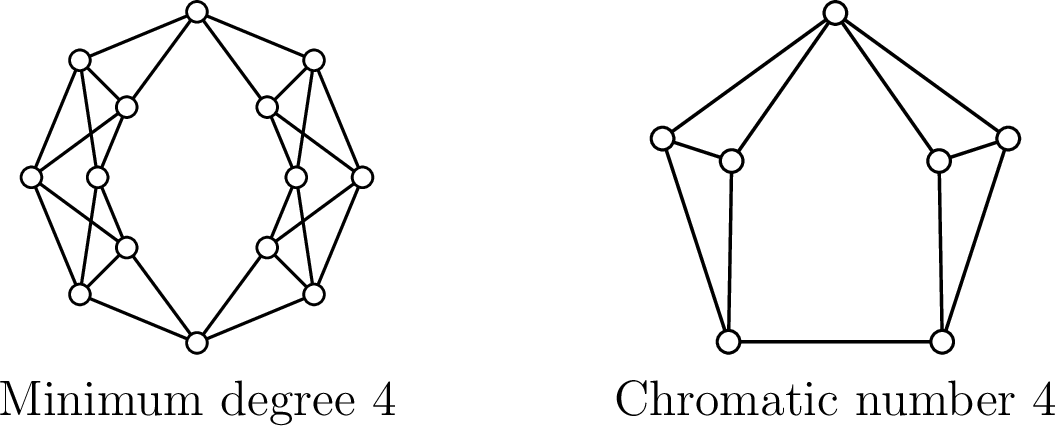
Figure 1: Graphs with no 3-connected subgraph.
Despite recent progress on related questions, there is no available proof that the number \(5\) of colours can be improved. The objective of this paper is to prove the following theorem that implies that every fragile graph is 4-colourable. It was announced without proof in [2] (which also contains a thorough literature review) and was independently rediscovered by the first two and last two authors of this article.
Theorem 2. For all \(m\geq 4\), every graph with chromatic number at least \(m+1\) has a 3-connected subgraph with chromatic number at least \(m\).
Theorem 2 is best possible as shown by the graph in Figure [f:wheel]. The proof of Theorem 2 is given in Section 2. Several remarks and open questions are presented in Section 3.
2 Proof of Theorem 2↩︎
For every integer \(m\geq 4\), a graph \(G\) is \(m\)-fragile if all 3-connected subgraphs of \(G\) are \((m-1)\)-colourable. Observe that a fragile graph is \(m\)-fragile for all \(m\geq 4\). 2 can be rephrased as: for all \(m\geq 4\), every \(m\)-fragile graph is \(m\)-colourable. To prove 2, we shall establish the following stronger statement. By a \(k\)-colouring of a graph \(G\), we mean a function \(c\) that associates to each vertex of \(G\) an integer in \(\{1, \dots, k\}\) and such that for all edges \(xy\) of \(G\), \(c(x)\neq c(y)\).
Theorem 3. For every integer \(m\geq 4\), every \(m\)-fragile graph \(G\) satisfies the following four conditions.
For all non-adjacent \(x, y\in V(G)\), \(G\) admits an \(m\)-colouring \(c\) such that \(c(x) = c(y)\).
For all distinct \(x, y \in V(G)\), \(G\) admits an \(m\)-colouring \(c\) such that \(c(x) \neq c(y)\).
For all distinct \(x, y, z \in V(G)\), \(G\) admits an \(m\)-colouring \(c\) such that \(c(x) \notin \{c(y), c(z)\}\).
For all distinct \(x, y, z \in V(G)\) that are not all pairwise adjacent, \(G\) admits an \(m\)-colouring \(c\) such that \(|\{c(x), c(y), c(z)\}| = 2\).
Proof. We proceed by induction on \(|V(G)|\). If \(|V(G)| \leq 3\), then \(G\) obviously satisfies conditions [c1]–3. For the induction step, suppose \(|V(G)|\geq 4\) and that the statement holds for every graph with fewer vertices than \(G\).
If \(G\) is 3-connected, then \(G\) satisfies conditions [c1]–3 because by assumption \(G\) is \((m-1)\)-colourable. So \(G\) can be coloured with colours 1 to \(m-1\), and colour \(m\) is available to satisfy any of the conditions [c1]–3 (for instance \(x\) and \(y\) can be recoloured with colour \(m\) to satisfy [c1]). Hence we may assume from here on that \(G\) is not 3-connected.
Since \(G\) is not 3-connected, there exist two induced subgraphs \(G_1, G_2\) of \(G\) such that \(V(G) = V(G_1) \cup V(G_2)\), \(E(G) = E(G_1) \cup E(G_2)\), \(V(G_1) \setminus V(G_2) \neq \emptyset\), \(V(G_2) \setminus V(G_1) \neq \emptyset\), and \(S = V(G_1) \cap V(G_2)\) has size at most 2. Moreover, since \(G\) is \(m\)-fragile, \(G_1\) and \(G_2\) are also \(m\)-fragile and, as \(|V(G_1)|, |V(G_2)| < |V(G)|\), we may apply the induction hypothesis to both \(G_1\) and \(G_2\).
If \(S= \emptyset\), the induction step is obvious and we omit the details. So we may set \(S = \{u, v\}\) (possibly \(u =v\)). We have to prove that for each of the precolouring conditions \(C\) among [c1]–3 on any given set \(X \subseteq V(G)\) (namely, \(X=\{x, y\}\) for conditions [c1] and [c2] and \(X=\{x, y, z\}\) for conditions [c3] and 3) some appropriate 4-colouring exists. Suppose first that \(X\subseteq V(G_1)\). Then, by the induction hypothesis, \(G_1\) admits a colouring \(c_1\) that satisfies \(C\). By applying [c1] or [c2] to the vertices \(u\) and \(v\) of \(G_2\) (or trivially if \(u=v\)), and up to a relabeling of the colours, we can force a colouring \(c_2\) of \(G_2\) such that \(c_2(u) = c_1(u)\) and \(c_2(v) = c_1(v)\). Note that the case when \(uv\) is an edge corresponds to the usual amalgamation of two colourings on a clique cutset. Hence, \(c_1 \cup c_2\) is a colouring of \(G\) that satisfies \(C\). The proof is similar when \(X \subseteq V(G_2)\). Hence, from here on, we may assume that \[\text{X intersects both V(G_1) \setminus V(G_2) and V(G_2) \setminus V(G_1). }\]
We now prove four claims, from which Theorem [thm:main2] trivially follows. Their proofs are easy when \(u=v\), so we omit this case and assume \(u\neq v\). Note that, unless specified otherwise, we shall make no assumption on whether \(u\) and \(v\) are adjacent.
Claim 1. The graph \(G\) satisfies [c1].
Proof. By (\(\star\)), we may assume that \(x\in V(G_1)\setminus V(G_2)\) and \(y\in V(G_2)\setminus V(G_1)\). We build three colourings \(a_1\), \(b_1\) and \(c_1\) of \(G_1\) and three colourings \(a_2\), \(b_2\) and \(c_2\) of \(G_2\) that are represented in Figure [f:c1] for the reader’s convenience.
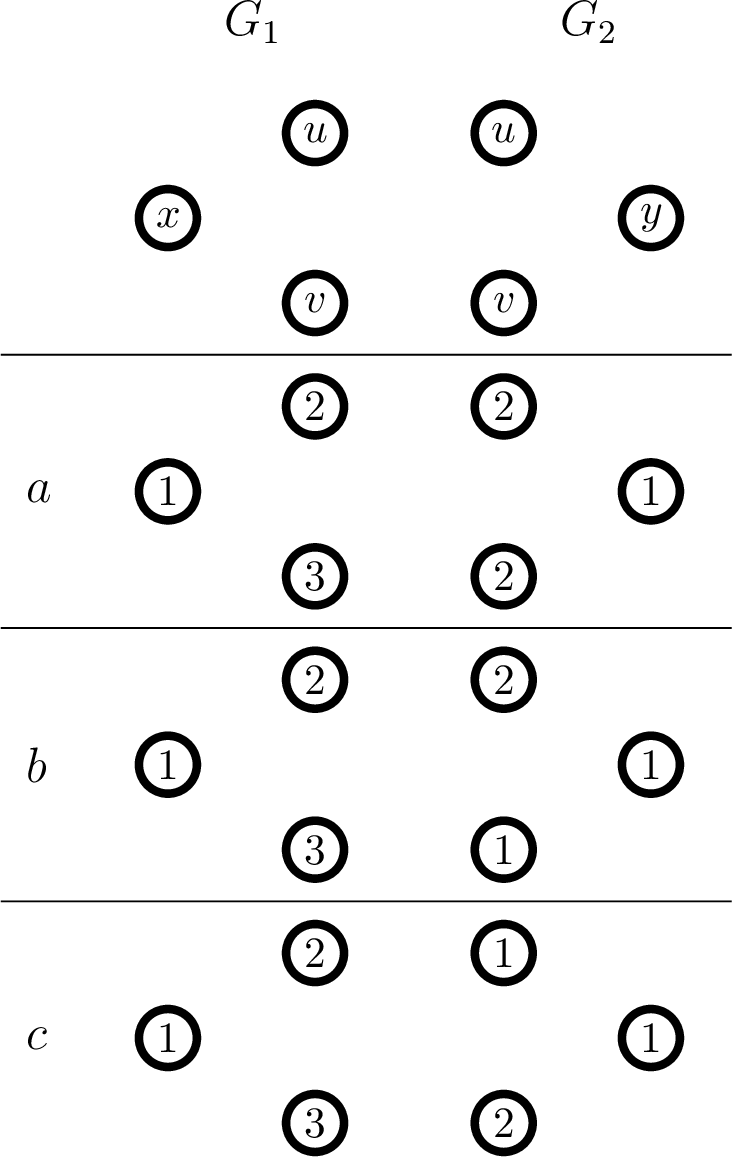
Figure 2: Colourings obtained in the proof of 1.
By [c3] applied to \(x, u, v\) (in this order) in \(G_1\), we obtain a colouring \(a_1\) of \(G_1\) such that \(a_1(x) \notin \{a_2(u), a_2(v)\}\). Similarly, we obtain a colouring \(a_2\) of \(G_2\) such that \(a_2(y) \notin \{a_2(u), a_2(v)\}\). Up to a relabeling, we may assume that \(a_1(x) = a_2(y) = 1\), \(a_1(u) = a_2(u) = 2\) and \(a_1(v), a_2(v) \in \{2, 3\}\). If \(a_1(v) = a_2(v)\), then \(a_1 \cup a_2\) is a colouring of \(G\) that satisfies [c1]. Hence, up to symmetry, we may assume that \(a_1(v) = 3\) and \(a_2(v) = 2\).
By [c3] applied to \(u, x, v\) in \(G_1\), we obtain a colouring \(b_1\) of \(G_1\) such that \(b_1(u) \notin \{b_1(x), b_1(v)\}\). Similarly, we obtain a colouring \(b_2\) of \(G_2\) such that \(b_2(u) \notin \{b_2(y), b_2(v)\}\). Up to a relabeling, we may assume that \(b_1(x) = b_2(y) = 1\), \(b_1(u) = b_2(u) = 2\) and \(b_1(v), b_2(v) \in \{1, 3\}\). If \(b_1(v) = b_2(v)\), then \(b_1 \cup b_2\) is a colouring of \(G\) that satisfies [c1]. Hence, we may assume that \(b_1(v) \neq b_2(v)\). If \(b_2(v) = 3\), then \(a_1 \cup b_2\) is a colouring of \(G\) that satisfies [c1]. Hence, we may assume that \(b_1(v) = 3\) and \(b_2(v) = 1\).
By [c3] applied to \(v, x, u\) in \(G_1\), we obtain a colouring \(c_1\) of \(G_1\) such that \(c_1(v) \notin \{c_1(x), c_1(u)\}\). Similarly, we obtain a colouring \(c_2\) of \(G_2\) such that \(c_2(v) \notin \{c_2(y), c_2(u)\}\). Up to a relabeling, we may assume that \(c_1(x) = 1\) and either \(c_1(u) = 1\) and \(c_1(v) = 2\) or \(c_1(u) = 2\) and \(c_1(v) = 3\). Up to a relabeling, we may also assume that \(c_2(y) = 1\) and either \(c_2(u) = 1\) and \(c_2(v) = 2\) or \(c_2(u) = 2\) and \(c_2(v) = 3\). If \(c_1(u) = c_2(u)\), then \(c_1 \cup c_2\) is a colouring of \(G\) that satisfies [c1]. Hence, we may assume that \(c_1(u) \neq c_2(u)\). If \(c_2(u) = 2\) (and so \(c_2(v) = 3\)), then \(a_1 \cup c_2\) is a colouring of \(G\) that satisfies [c1]. Hence, we may assume that \(c_1(u) = 2\), \(c_1(v) = 3\), \(c_2(u) = 1\) and \(c_2(v) = 2\).
By 3 applied to \(x, u, v\) in \(G_1\), we obtain a colouring \(d_1\) of \(G_1\) such that \(|\{d_1(x), d_1(u), d_1(v)\}| = 2\) (note that \(x\), \(u\) and \(v\) are not pairwise adjacent because \(a_2(u)=a_2(v)\) implies \(uv\notin E(G)\)). Up to a relabeling, we may assume that \(d_1(x) = 1\) and \(\{d_1(x), d_1(u), d_1(v)\} = \{1, 2\}\). If \(d_1(u) = 1\) and \(d_1(v) = 2\), then \(d_1 \cup c_2\) satisfies [c1]. And if \(d_1(u) = 2\) and \(d_1(v) = 1\), then \(d_1 \cup b_2\) satisfies [c1]. Finally, if \(d_1(u) = 2\) and \(d_1(v) = 2\), then \(d_1 \cup a_2\) satisfies [c1]. The claim is proved. ◻
Claim 2. The graph \(G\) satisfies [c3].
Proof. If \(x\in \{u, v\}\) (say \(x=u\) up to symmetry), then by (\(\star\)) we may assume that \(y\in V(G_1) \setminus V(G_2)\) and \(z \in V(G_2) \setminus V(G_1)\). By [c3] applied separately to \(x\), \(v\) and \(y\) in \(G_1\) and to \(x\), \(v\) and \(z\) in \(G_2\), we obtain up to a relabeling a colouring \(a_1\) of \(G_1\) and a colouring \(a_2\) of \(G_2\) such that \(a_1(x)=a_2(x) = 1\), \(a_1(v)=a_2(v) = 2\), \(a_1(y)\neq 1\) and \(a_2(z)\neq 1\). Hence, \(a_1\cup a_2\) is a colouring of \(G\) that satisfies \(\ref{c3}\). We may therefore assume that \(x\notin \{u, v\}\), and so up to symmetry that \(x\in V(G_1) \setminus V(G_2)\).
Hence, by (\(\star\)) and up to symmetry, we may restrict our attention to the following two cases.
Case 1: \(x\in V(G_1) \setminus V(G_2)\) and \(y, z \in V(G_2)\).
If \(uv\in E(G)\), then by [c3] applied to \(x\), \(u\) and \(v\) and up to a relabeling, there exists a colouring \(a_1\) of \(G_1\) such that \(a_1(x) = 1\), \(a_1(u)=2\), and \(a_1(v)=3\). We claim that there exists a colouring \(a_2\) of \(G_2\) that requires at most \(m-1\) colours for \(u\), \(v\), \(y\), \(z\). If \(m\geq 5\), this is trivial, so suppose \(m=4\). Then the graph induced by \(u\), \(v\), \(y\) and \(z\) is not a complete graph on four vertices, because such a graph is 3-connected with chromatic number 4 and would imply that \(G\) is not \(m\)-fragile. Hence, either \(|\{u, v, y, z\}|\leq 3\) or there are non-adjacent vertices among \(u\), \(v\), \(y\) and \(z\). In either case, there exists a colouring \(a_2\) of \(G_2\) that requires at most \(m-1=3\) colours for \(u\), \(v\), \(y\), \(z\) (trivially if \(|\{u, v, y, z\}|\leq 3\) or by applying [c1] to a non-edge otherwise). This proves our claim. Up to a relabeling, we may assume that \(a_2(u)=2\), \(a_2(v)=3\) and \(\{a_2(y), a_2(z)\} \subseteq \{2, \dots, m\}\). Hence, \(a_1\cup a_2\) is a colouring of \(G\) satisfying [c3]. We may therefore assume from here on that \(uv\notin E(G)\).
Suppose that there exists a colouring \(a_1\) of \(G_1\) such that \(a_1(x) \neq a_1(u) = a_1(v)\). So, up to a relabeling, we may assume \(a_1(x)=1\) and \(a_1(u)=a_1(v)=2\). Then by [c1] applied to \(u\) and \(v\) in \(G_2\), there exists a colouring \(a_2\) of \(G_2\) such that \(a_2(u)=a_2(v)\). Hence, \(|\{a_2(u), a_2(v), a_2(y), a_2(z)\}|\leq 3\). So, up to a relabeling, we may assume that \(a_2(u) = a_2(v) = 2\) and \(\{a_2(y), a_2(z)\} \subseteq \{2, 3, 4\}\). So \(a_1 \cup a_2\) is a colouring of \(G\) that satisfies [c3]. We may therefore assume that no colouring as \(a_1\) exists.
Hence, when applying [c3] to \(x\), \(u\) and \(v\), up to a relabeling, we obtain a colouring \(b_1\) of \(G_1\) such that \(b_1(x) =1\), \(b_1(u)=2\) and \(b_1(v)=3\). And when applying 3 to \(x\), \(u\) and \(v\) (which is allowed since \(uv\notin E(G)\)), up to a relabeling and to the symmetry between \(u\) and \(v\), we obtain a colouring \(c_1\) of \(G_1\) such that \(c_1 (x)=1\), \(c_1 (u)=1\) and \(c_1 (v)=2\).
By [c2] applied to \(u\) and \(v\), there exists a colouring \(d_2\) of \(G_2\) such that \(d_2(u)\neq d_2(v)\). If \(|\{d_2(u), d_2(v), d_2(y), d_2(z)\}| \leq 3\), then up to a relabeling, we may assume that \(d_2(u)=2\), \(d_2(v)=3\) and \(\{d_2(y), d_2(z)\}\subseteq \{2, 3, 4\}\), So \(b_1 \cup d_2\) is a colouring of \(G\) that satisfies [c3]. And if \(|\{d_2(u), d_2(v), d_2(y), d_2(z)\}| = 4\), then we may assume up to a relabeling that \(d_2(u)=1\), \(d_2(v)=2\), \(d_2(y)=3\) and \(d_2(z)=4\), so \(c_1\cup d_2\) is a colouring that satisfies [c3].
Case 2: \(x, y\in V(G_1) \setminus V(G_2)\) and \(z \in V(G_2) \setminus V(G_1)\).
By [c3] applied to \(x\), \(y\) and \(u\), up to a relabeling, we obtain a colouring \(a_1\) of \(G_1\) such that \(a_1(x) =1\), \(a_1(y)=2\) and \(a_1(u)\in \{2, 3\}\). If \(a_1(v)\neq 1\), then colour 1 is not used on \(u\) or \(v\) under \(a_1\). By [c1] or [c2] applied to \(u\) and \(v\), we obtain up to a relabeling a colouring \(a_2\) of \(G_2\) such that \(a_2(u)=a_1(u)\) and \(a_2(v)=a_1(v)\). Thus, colour 1 is not used on \(u\) or \(v\) under \(a_2\) either and so, up to a relabeling, we may assume that \(a_2(z) \neq 1\). Hence \(a_1 \cup a_2\) is a colouring of \(G\) that satisfies [c3]. We may therefore assume that \(a_1(v)=1\).
By [c3] applied to \(v\), \(u\) and \(z\), up to a relabeling, we obtain a colouring \(b_2\) of \(G_2\) such that \(b_2(v) =1\), \(b_2(u)= a_1(u)\) and \(b_2(z)\neq 1\). Hence \(a_1 \cup\,b_2\) is a colouring of \(G\) that satisfies [c3]. ◻
Claim 3. The graph \(G\) satisfies [c2].
Proof. By Claim 2, we may apply [c3] to \(x\), \(y\) and any vertex of \(G\). We obtain a colouring of \(G\) that satisfies [c2]. ◻
Claim 4. The graph \(G\) satisfies 3.
Proof. By (\(\star\)), we may assume that \(x\in V(G_1)\setminus V(G_2)\) and \(y \in V(G_2)\setminus \{u\}\) and \(z\in V(G_2) \setminus V(G_1)\).
Suppose that \(uv\in E(G)\). Then by [c3] applied to \(x\), \(u\) and \(v\) and up to a relabeling, there exists a colouring \(a_1\) of \(G_1\) such that \(a_1(x)=1\), \(a_1(u)=2\) and \(a_1(v)=3\). By [c3] applied to \(u\), \(y\) and \(z\) (that are distinct since \(y\neq u\) and \(z\in V(G_2) \setminus V(G_1)\)) and up to a relabeling, we obtain a colouring \(a_2\) of \(G_2\) such that \(a_1(u)=2\), \(a_1(v)=3\) and \(\{a_2(y), a_2(z)\}\) is either \(\{3, 1\}\), \(\{3\}\) or \(\{4\}\). In either case, \(a_1\cup a_2\) is a colouring of \(G\) satisfying 3. We may therefore assume from here on that \(uv\notin E(G)\).
Suppose that there exists a colouring \(a_1\) of \(G_1\) such that \(a_1(x) \neq a_1(u) = a_1(v)\). Then up to a relabeling we may assume that \(a_1(x)=1\) and \(a_1(u)=a_1(v) = 2\). By [c1] applied to \(u\) and \(v\) in \(G_2\), there exists up to a relabeling a colouring \(a_2\) of \(G_2\) such that \(a_2(u)=a_2(v) =2\). If \(a_2(y)=a_2(z)\), then up to relabeling, we may assume that \(a_2(y)=a_2(z)\neq 1\), so 3 is satisfied by \(a_1 \cup a_2\). And if \(a_2(y)\neq a_2(z)\), then up to a relabeling, we may assume \(a_2(y) = 1\) or \(a_2(z) = 1\), and 3 is again satisfied by \(a_1\cup a_2\). We may therefore assume that no colouring as \(a_1\) exists.
Hence, when applying [c3] to \(x\), \(u\) and \(v\), up to a relabeling, we obtain a colouring \(b_1\) of \(G_1\) such that \(b_1(x) =1\), \(b_1(u)=2\) and \(b_1(v)=3\). And when applying 3 to \(x\), \(u\) and \(v\) (which is allowed since \(uv\notin E(G)\)), up to a relabeling and to the symmetry between \(u\) and \(v\), we obtain a colouring \(c_1\) of \(G_1\) such that \(c_1 (x)=1\), \(c_1 (u)=1\) and \(c_1 (v)=2\).
On the other hand, by [c2] applied to \(u\) and \(v\), there exists a colouring \(d_2\) of \(G_2\) such that \(d_2(u)\neq d_2(v)\). If \(d_2(y)= d_2(z)\), then up to a relabeling, we may assume that \(d_2(u)=2\), \(d_2(v)=3\) and \(d_2(y) \neq 1\). Thus, \(b_1\cup d_2\) is a colouring that satisfies 3. Hence, from here on, we may assume that \(d_2(y) \neq d_2(z)\).
If \(|\{d_2(u), d_2(v), d_2(y), d_2(z)\}| \geq 3\), then we may assume up to a relabeling that \(d_2(u)=2\), \(d_2(v)=3\) and \(1\in \{d_2(y), d_2(z)\}\), so \(b_1\cup d_2\) is a colouring that satisfies 3. If \(|\{d_2(u), d_2(v), d_2(y), d_2(z)\}| = 2\), then up to a relabeling, we may assume that \(d_2(u)=1\), \(d_2(v)=2\), so that \(\{d_2(y), d_2(z)\} = \{1, 2\}\). So \(c_1 \cup d_2\) is a colouring of \(G\) that satisfies 3. ◻
3 Conclusion and open questions↩︎
We collect here several remarks and open questions.
3.1 Fragile graphs have average degree less than 5↩︎
As announced in the introduction, we recall the proof that every fragile graph \(G\) on at least four vertices satisfies \(|E(G)| \leq 2.5 |V(G)| -5\). When \(G\) has 4 vertices, the inequality holds since the graph on 4 vertices and 6 edges is a complete graph and is 3-connected. For the induction step, we decompose \(G\) into \(G_1\) and \(G_2\) as in the previous section. If \(|V(G_1)| \leq 3\), then \(G\) contains a vertex \(x\) of degree at most 2. Hence, \[|E(G)| \leq |E(G\setminus x)| + 2 \leq 2.5|V(G\setminus x)| - 5 + 2 = 2.5(|V(G)| -1) -3 \leq 2.5|V(G)| -5.\] We may therefore assume that \(|V(G_1)| \geq 4\) and symmetrically \(|V(G_2)| \geq 4\). Hence the induction hypothesis can be applied to both \(G_1\) and \(G_2\) so that the result follows from these inequalities:
\[\begin{align} |E(G)| &\leq |E(G_1)| + |E(G_2)| \\ &\leq 2.5|V(G_1)| - 5 + 2.5|V(G_2)| - 5 \\ &= 2.5(|V(G_1)| + |V(G_2)|) - 10 \\ &\leq 2.5 (|V(G)| +2) -10 \\ &= 2.5 |V(G)| - 5. \end{align}\]
3.2 Girth conditions↩︎
It is easy to prove by induction that every fragile graph of girth at least 4 on at least 3 vertices satisfies \(|E(G)| \leq 2 |V(G)| - 4\) (the proof is as in 3.1). This implies that every fragile graph with girth at least 4 contains a vertex of degree at most 3, so is 4-colourable. We tried to improve this bound, but we instead found a fragile graph with girth 4 and chromatic number 4, as we now present.
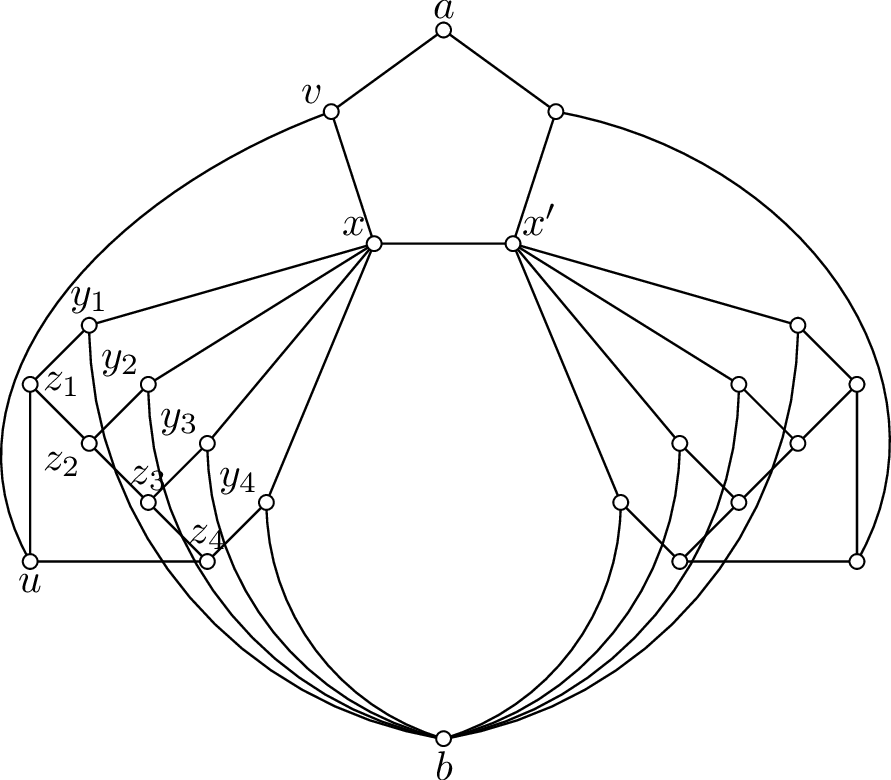
Figure 3: The graph \(G_1\).
Let \(G_1\) be the graph represented in Figure 3. It has girth 4 and is 2-degenerate; so in particular it is fragile and has chromatic number at most 3. For all 3-colourings of \(G_1\), vertices \(a\) and \(b\) receive different colours. Indeed, suppose for a contradiction that for some 3-colouring of \(G_1\), \(a\) and \(b\) receive the same colour, say colour 1. Then, one of \(x\) and \(x'\), say \(x\) up to symmetry, must receive a colour different from 1, say colour 2. So, the vertices \(y_1\), …, \(y_4\) must all receive the same colour, say colour 3. It follows that the vertices \(z_1, \dots, z_4\) are coloured with colour 1 and 2 alternately. Hence, \(u\) receives colour 3. Now, \(v\) has three neighbors, namely \(a\), \(x\) and \(u\) that are coloured with colours 1, 2 and 3 respectively, a contradiction.
It follows that the triangle-free graph \(G_2\) represented in Figure 4 is not 3-colourable, but it is fragile since \(\{a',b'\}\) is a cutset, and \(G_1\) is 2-degenerate even if two vertices adjacent to \(a\) and \(b\) are added.
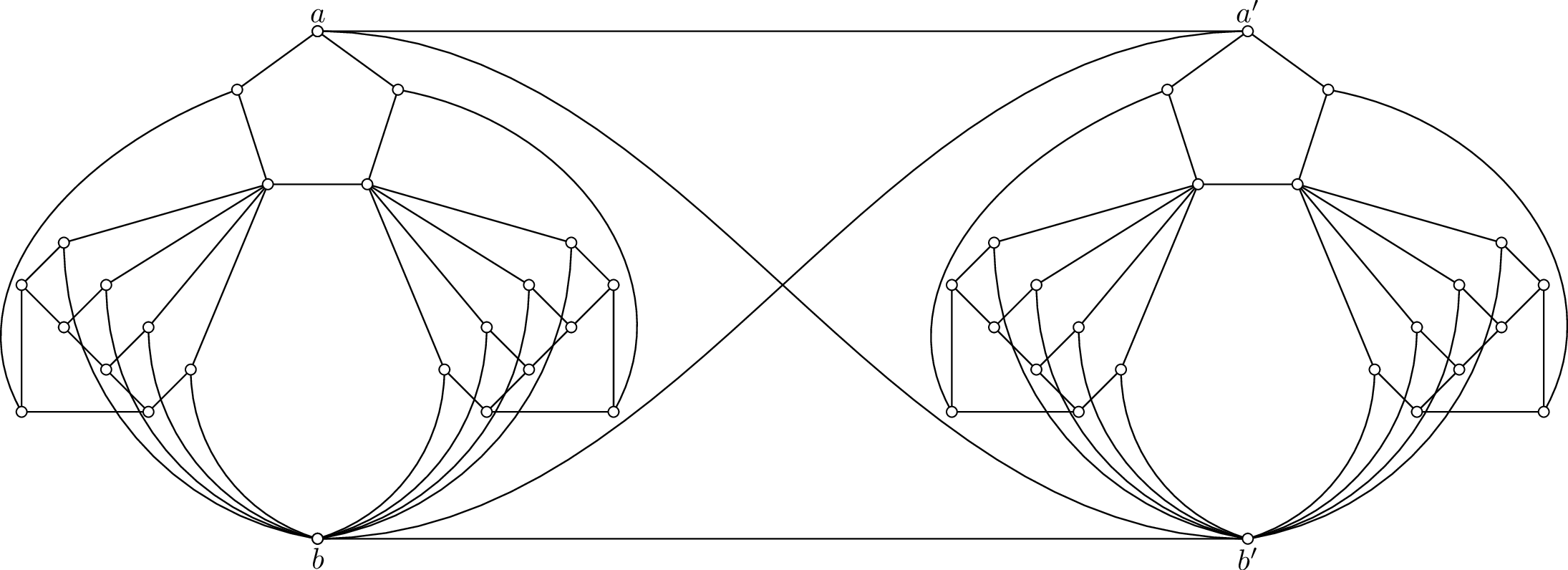
Figure 4: The graph \(G_2\).
We could also obtain a fragile graph with no cycle of length 4 and chromatic number 4, see Figure 5.

Figure 5: A fragile graph with no cycle of length 4 and chromatic number 4.
This raises the following question: Is there a finite girth that makes fragile graphs 3-colourable? A possible approach could be to prove that if the girth of a fragile graph is large enough, then the graph is 2-degenerate. But this approach fails because of the following construction. Consider an integer \(g\geq 3\) and a connected cubic graph \(G\) of girth \(g\) (this exists, see for instance [3]). Remove an edge \(uv\) of \(G\). This yields a 2-degenerate, and therefore fragile graph. Consider a copy \(G'\) of \(G\setminus uv\), with the vertices \(u'\) and \(v'\) corresponding to \(u\) and \(v\) respectively. Now add an edge \(uu'\) and an edge \(vv'\). The obtained graph is fragile, cubic and has girth \(g\).
Trivially, a graph \(G\) is fragile if and only if every subgraph \(H\) of \(G\) is either on at most 3 vertices or admits a cutset of size at most 2. In fragile graphs of girth at least 4, one can further impose the cutset to be an independent set.
Lemma 1. A graph \(G\) with girth at least 4 is fragile if and only if every subgraph \(H\) of \(G\) is either on at most 2 vertices or admits an independent cutset of size at most 2.
Proof. We prove the statement by induction on \(|V(G)|\). The equivalence can be checked to hold on graphs of up to 3 vertices. If \(|V(G)|\geq 4\), then since \(G\) is not 3-connected, it admits a cutset \(S\) of size at most 2. Suppose that \(S\) is not independent, so \(S=\{u, v\}\) and \(uv\in E(G)\). Let \(C\) be a connected component of \(G\setminus S\). Since \(G\) has girth at least 4, no vertex of \(C\) is adjacent to both \(u\) and \(v\). Hence, if \(|C| = 1\), \(G\) admits a cutset of size 1 (and therefore independent). So we may assume that \(|C| \geq 2\). So, by the induction hypothesis, \(G[S \cup C]\) admits an independent cutset \(S'\). It is easy to check that \(S'\) is also a cutset of \(G\). ◻
3.3 Algorithms↩︎
By subdividing twice every edge of any graph \(G\), a fragile graph \(G'\) is obtained. Poljak [4] proved that \(\alpha(G') = \alpha(G) + |E(G)|\). It follows that a polynomial-time algorithm that computes a maximum independent set for any fragile graph would yield a similar algorithm for all graphs. This proves that computing a maximum independent set in a fragile graph is NP-hard.
We also observe that, in \(G'\), every edge \(uv\) becomes a path \(ux_{uv}y_{uv}v\). Consider the graph \(G''\) obtained from \(G'\) by adding, for every vertex \(x_{uv}\), a new vertex \(x'_{uv}\) adjacent to \(u\), \(x_{uv}\) and \(y_{uv}\). It is easy to check that \(G''\) is fragile and for all 3-colourings of \(G''\) and all edges \(uv\) of \(G\), \(u\) and \(v\) have different colours (in \(G''\)). It follows that if \(G''\) is 3-colourable, then so is \(G\). Conversely it is easy to check that if \(G\) is 3-colourable, so is \(G''\). This proves that deciding whether a fragile graph is 3-colourable is NP-complete. By the same kind of argument, we can prove that deciding whether a graph is 3-colourable stays NP-complete even when we restrict ourselves to fragile triangle-free graphs. To see this, pick any graph \(G\), remove all edges \(uv\), and replace them by a copy of the graph \(G_1\) from Figure 3 with \(a\) identified to \(u\) and \(b\) identified to \(v\). This yields a triangle-free fragile graph that is 3-colourable if and only if \(G\) is 3-colourable.
Our proof that every fragile graph is 4-colourable yields an algorithm that actually computes a 4-colouring. A crude implementation of this algorithm would run in exponential time, but it is easy to turn it into a polynomial time algorithm by maintaining for each 2-tuples and 3-tuples \(X\) of vertices of the input graph, a colouring satisfying the constraints [c1]–3 when applicable to \(X\).
Acknowledgements↩︎
Édouard Bonnet, Carl Feghali, Stéphan Thomassé and Nicolas Trotignon are partially supported by the French National Research Agency under research grant ANR DIGRAPHS ANR-19-CE48-0013-01, ANR Twin-width ANR-21-CE48-0014-01 and the LABEX MILYON (ANR-10-LABX-0070) of Université de Lyon, within the program Investissements d’Avenir (ANR-11-IDEX-0007) operated by the French National Research Agency (ANR). Tung Nguyen and Paul Seymour are partially supported by AFOSR grants A9550-19-1-0187 and FA9550-22-1-0234, and by NSF grants DMS-1800053 and DMS-2154169. Alex Scott is supported by EPSRC grant EP/X013642/1. Part of this work was done when Nicolas Trotignon visited Princeton University with generous support of the H2020-MSCA-RISE project CoSP- GA No. 823748.