Electromagnetic Counterparts Powered by Kicked Remnants of Black Hole Binary Mergers in AGN Disks
November 17, 2023
Abstract
The disk of an active galactic nucleus (AGN) is widely regarded as a prominent formation channel of binary black hole (BBH) mergers that can be detected through gravitational waves (GWs). Besides, the presence of dense environmental gas offers the potential for an embedded BBH merger to produce electromagnetic (EM) counterparts. In this paper, we investigate EM emission powered by the kicked remnant of a BBH merger occurring within the AGN disk. The remnant BH will launch a jet via accreting magnetized medium as it traverses the disk. The resulting jet will decelerate and dissipate energy into a lateral cocoon during its propagation. We explore three radiation mechanisms of the jet-cocoon system: jet breakout emission, disk cocoon cooling emission, and jet cocoon cooling emission, and find that the jet cocoon cooling emission is more likely to be detected in its own frequency bands. We predict a soft X-ray transient, lasting for \(O(10^3)\text{ s}\), to serve as an EM counterpart, of which the time delay \(O(10)~days\) after the GW trigger contributes to follow-up observations. Consequently, BBH mergers in the AGN disk represent a novel multimessenger source. In the future, enhanced precision in measuring and localizing GWs, coupled with diligent searches for such associated EM signal, will effectively validate or restrict the origin of BBH mergers in the AGN disk.
1 Introduction↩︎
Since the first observation of gravitational wave (GW) by the advanced LIGO/Virgo GW detectors [1], binary black hole (BBH) mergers are emerging as a predominant category of GW sources [2]–[4]. Future GW detectors are expected to detect a substantial number (e.g., \(\sim 10^4-10^5\) events per year) of BBH mergers [5], [6]. Various formation channels have been proposed to account for BBH mergers ([7], [8]; see [9] for a list). Among these channels, the disk of an active galactic nucleus (AGN) is garnering significant attention in recent studies, as the BBH merger event GW190521 [10], along with a plausible electromagnetic (EM) counterpart ZTF19abanrhr [11], indicates an AGN disk environment origin.
Black hole binaries are expected to widely exist in the AGN disk [12]–[19]. Several mechanisms, e.g., gas torque [20]–[24], binary-single interaction [16], [25], [26], and GW radiation [27], can induce orbital hardening, ultimately leading to BBH mergers. Due to the unique nature of an AGN (strong gravity from a central supermassive black hole, high stellar density in the nuclear cluster, and the presence of an accretion disk), BBH mergers in the AGN disk exhibits several peculiarities, such as hierarchical mergers [28], [29] or eccentric mergers [26], [30]. The merger rate of BBH with an AGN disk origin ranges from \(O(10^{-3})\) to \(O(10^2)~\rm{Gpc}^{-3}~\rm{yr}^{-1}\) (see Table 1 in Arca?, Sedda23?). Despite significant uncertainty, these mergers can make a substantial contribution to the overall population with the inferred redshift-dependent merger rate \(17.9-44~\rm{Gpc}^{-3}~\rm{yr}^{-1}\) [31]. Therefore, the AGN disk formation channel demonstrates great importance in the era of GW astronomy.
In addition to the distinctive GW signals, the gas-rich environment of AGN disk provides an opportunity for the embedded BBHs to generate electromagnetic (EM) emission, elevating these BBHs to multimessenger sources. In turn, the identification of an EM counterpart would strongly support the AGN disk formation channel [32], [33]. Preliminarily, in terms of energy, EM emission from the binaries is potentially observable, as the total power of energy release during the BBH accretion process exceeds the AGN background luminosity [12], [13]. Various specific emission processes have been proposed to predict the EM counterparts [11], [34]–[39], with diverse emission properties across different models. Though several candidates are reported [40], no EM counterpart to BBH mergers in the AGN disk has been confirmed so far, thus preventing a test of existing models and leaving room for new ones.
In this paper, we investigate a plausible emission process by concretely considering the accretion of BHs both during the inspiral phase and post-merger. In our model, a jet launched by the kicked merger remnant BH acts as an emission source. We study the propagation of the jet within AGN disk and the subsequent emergence of resulting emission, with a specific focus on its detectability.1 This paper is organized as follows. In Section 2, we discuss the circum-binary environment of an embedded BBH merger and the properties of GW recoil kick impacted on the remnant. We investigate the formation and propagation of a jet driven by the kicked remnant in Section 3. We next explore three emission processes of the jet-cocoon system in Section 4. Several discussions are presented in Section 5, particularly involving the detectability of associated EM counterparts in Section 5.1. We summarize our conclusions in Section 6. Symbols \(c\) and \(G\) in this paper denotes the speed of light and the gravitational constant, respectively.
2 BBH merges and kicked in AGN disk environment↩︎
The AGN disk can be described as a viscous accretion disk with three parameters, i.e., the SMBH mass \(M\), the mass inflow rate \(\dot{M}\), and the viscosity parameter \(\alpha\) [41]; meanwhile, the outer region of the AGN disk is gravitationally unstable to impact the disk structure [42]. Many plausible theoretical models have been proposed to construct a quasi-stationary self-gravitating accretion disk e.g. [43], [44], [45], [46] et al., among which we adopt the widely used SG [43] model and TQM [44] model in this work, and we refer to Equation (26)-(29) of [47] for disk equations.
2.1 Circum-binary environment of a BBH merger↩︎
As the gas in an AGN disk is differentially rotating and its density is high, a circularized disk would form around the embedded BH with initial mass inflow rate greatly exceeding the Eddington accretion rate, \(\dot{M}_{\rm{Edd}}=L_{\rm{Edd}} c^2 / \eta\), where we set the radiation efficiency \(\eta=0.1\) and \(L_{\rm{Edd}}=4\pi G m m_pc/\sigma_T=1.26\times10^{40}m_2\; \rm{erg\,s}^{-1}\) [48]–[50]. Similarly, a circum-binary disk would form around the embedded binary black hole. In addition, two circum-BH disks severally form around the two components (the accreting structure is visible in recent numerical simulations, e.g. [20], [51], [52]). We employ the Bondi-Holye-Lyttleton (BHL) formulation [53], \(\dot{M}_{\rm{BHL}}=4 \pi G^2 m_{\rm{bin}}^2 \rho_{\rm{AGN}} /(v_{\rm{rel}}^{2}+c_{\rm{s,AGN}}^{2} )^{3/2}\), where \(m_{\rm{bin}}\) is the total mass of the BBH, \(\rho_{\rm{AGN}}\) and \(c_{\rm{s,AGN}}\) are the density and sound speed of AGN disk, \(v_{\rm{rel}}\) is the relative velocity between the BBH center of mass and the ambient gas, to estimate the mass captured rate of the BBH system and the initial mass inflow rate of the circum-binary disk. For the case of the binary separation \(a_{\rm{bin}}\) being much smaller than the outer boundary of the circum-binary disk \(r_{\rm{obd}}\), the BBH can be approximated as a point source and the circum-binary disk would evolve akin to a circum-single disk [35], though the mass rate would be reduced and evolve over time in the BBH system [22].
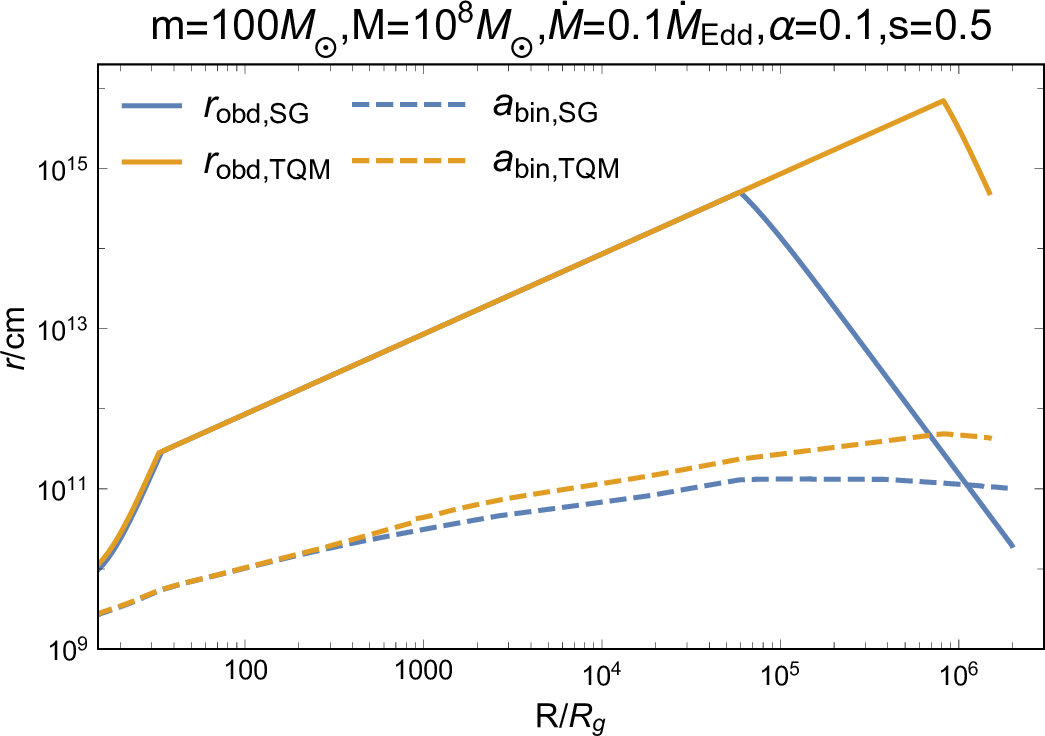
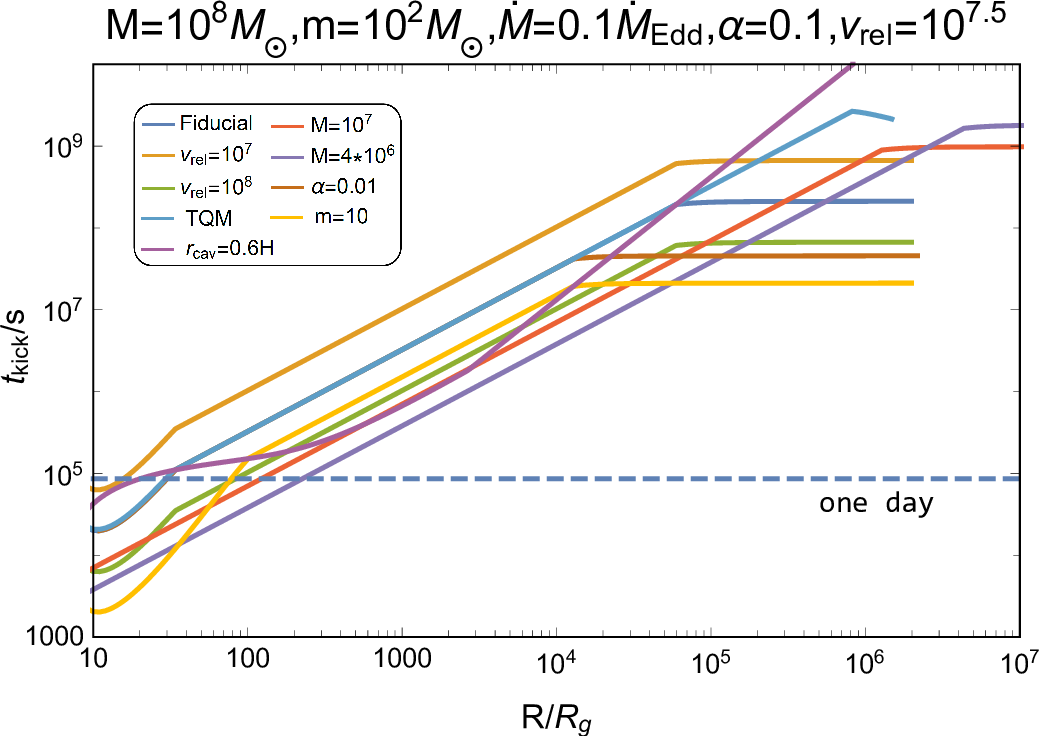
Figure 1: Properties of binary accretion and merger. The left panel shows the outer boundary radius of circum-binary disk \(r_{\rm{obd}}\), of which the calculations adopt [50], considering both the circularization due to angular momentum conservation of the BBH-captured AGN disk gas and the disk truncation by the heated outflow, and the critical binary separation \(a_{\rm{bin,cr}}\) as a function of AGN radius \(R\), scaled by gravitational radius \(R_{\rm{g}}=G M/c^2\); the fiducial parameters are \(m_{\rm{bin}}=100\rm{M}_{\odot}\), \(M=10^{8}\rm{M}_{\odot}\), \(\dot{M}=0.1 \dot{\rm{M}}_{\rm{Edd}}\), \(\alpha=0.1\), \(s=0.5\), where \(s\) is the power-law index of the radius-dependent circum-binary disk mass inflow rate. The blue and golden lines represent the AGN disk adopting SG and TQM model, respectively. We change all these parameters and find that the relative size between \(r_{\rm{obd}}\) and \(a_{\rm{bin,cr}}\) are preserved, i.e., \(a_{\rm{bin,cr}} \ll r_{\rm{obd}}\); so, for simplicity, only the fiducial case is shown. The right panel represents the timescale of a kicked merger remnant crossing the cavity, \(t_{\rm{kick}}\), under various system parameters (as shown in the inset); the fiducial case is the same, with \(v_{\rm{rel}} \sim v_{\rm{k}} = 10^{2.5}\rm{~km~s}^{-1}\) (\(\rm{cm~s}^{-1}\) in graph legend) adopting SG model. The blue dashed line represents the time equaling to one day..
As shown by [50], a hyper-Eddington circum-BH disk would launch powerful outflow to push out the surrounding gas, generating a low-density cavity to intermittently choke the effective accretion; in the same way, the embedded BBH would go through similar accretion processes. Meanwhile, the binary separation hardens due to GW radiation within the inspiral timescale [27], \[t_{\rm{GW}}=\frac{5}{128} \frac{c^{5} a_{\rm{bin}}^{4}}{G^{3} m_{\rm{bin}}^{3}}.\] We compare \(t_{\rm{GW}}\) with the cavity persistence timescale \(\sim t_{\rm{ref}}\), Equation (32) in [50], of each recurrent accretion process. For a BH binary system with an initial separation \(a_{\rm{bin}}\) satisfying \(t_{\rm{GW}}(a_{\rm{bin}})>t_{\rm{ref}}\), the BBH would not merge within one accretion episode, but continuously hardens via various mechanisms [16]; then, when \(a_{\rm{bin}}<a_{\rm{bin,cr}}\), where \(t_{\rm{GW}}(a_{\rm{bin,cr}})=t_{\rm{ref}}\), the BBH would undergo inspiral to merger just within one recurrent accretion process. As shown in Figure 1, the critical binary separation \(a_{\rm{bin,cr}}\) is much smaller than \(r_{\rm{obd}}\), thus, the binary can be treated as a single object and the whole accretion-feedback process is valid. Also, since \(a_{\rm{bin,cr}}\lesssim O(10^{11})\text{ cm}\), the BBH hardening is dominated by GW radiation, the other mechanisms, e.g., gas dynamical friction, binary–single interaction and torque from the circum-binary disk, can be ignored [16].
For a BBH merger occurring within one recurrent accretion process, the cavity persistence timescale is much longer than the timescale of outflow formation to open a cavity, which is estimated by the viscous timescale of the circularized circum-binary disk, \(t_{\rm{vis}}\), where \(t_{\rm{vis}}\lesssim0.1t_{\rm{ref}}\) [50]. Consequently, it is more probable for the merging BBH to reside in a low-density cavity rather than being surrounded by AGN disk gas. However, prior to the GW dominates over BBH hardening, binary-single interactions are frequent [16], leading to an appreciable probability of the BH binary undergoing a 3-body merger [26], i.e., the temporary BH binary merges in the chaotic 3-body system due to high binary orbital eccentricity decreasing the inspiral time. No work has been done to investigate the accretion process of such 3-body system. Although unproven, we propose that a stable circum-binary disk and outflow would not persist under the perturbation of a chaotic third companion, preventing the formation of a large-scale cavity in the 3-body system, and thereby the merger remnant would be encompassed by the AGN disk gas. Moreover, the study of accretion-induced outflow feedback relies on BH (BBH) systems that are co-rotating with the AGN disk [35], [50], [54], if the BH binary has a large velocity relative to the ambient gas, it remains unclear whether a stable circum-binary disk can form to open a cavity. Therefore, further exploration is required to elucidate the specific feedback mechanism.
In brief, at the time of a BBH merger via GW radiation in the AGN disk, the circum-binary environment could be either the AGN disk or the cavity, depending on whether a stable disk forms around the inspiral BH binary and an accretion-induced strong outflow is successfully generated.
2.2 GW kick on a BBH merger remnant↩︎
For a BBH binary with asymmetric components, the merger remnant would receive a recoil kick via anisotropic gravitational radiation during the final inspiral stage, where the kick velocity \(v_{\rm{k}}\) depends on the binary mass ratio and the BHs’ spin [55]–[58]. The velocity component caused by the mass unequal is [59] \[v_{\rm{m}}=A \frac{q^{2}(1-q)}{(1+q)^{5}}\left[1+B \frac{q}{(1+q)^{2}}\right],\] where \(q\) is the mass ratio of the lighter to the heavier BH, and \(A=1.2 \times 10^4 \rm{~km~s}^{-1}\), \(B=-0.93\). For the LIGO/Virgo detected events [2]–[4], \(v_{\rm{m}}\) of BBH mergers ranges from \(43\rm{~km~s}^{-1}\) to \(175\rm{~km~s}^{-1}\), with an average value \(109\rm{~km~s}^{-1}\). Also, the amplitude of \(v_{\rm{k}}\) demonstrates remarkable sensitivity to the BH spin and can scale up to \(O(10^3)\rm{~km~s}^{-1}\) [59], e.g., for the event GW190521 [10], \(v_{m}\sim 70 \rm{~km~s}^{-1}\) but \(v_{\rm{k}} > 200 \rm{~km~s}^{-1}\) when taking the effects of BH spin into account [60]. Since the components of the embedded BBH would inherently possess low spin [61], or spin rapidly, but of which the individual spin directions are misaligned with the binary orbital angular momentum [9], we set three values of \(v_{\rm{k}}= 10^2, 10^{2.5}, 10^3\rm{~km~s}^{-1}\) to study the kicked merger remnants of BBH with various mass ratio, spin magnitude and direction.
As demonstrated above, a BBH merger would take place in a low-density cavity provided that a stable circum-binary accretion disk exists during the binary inspiral phase; subsequently, the kicked merger remnant need traverse the cavity to re-enter the AGN disk environment. The radius of the cavity, \(r_{\rm{cav}}\), is determined by the specific properties of the accretion-induced outflow, which is about the order of BBH gravity radius [35], [50], i.e., min\(\left\lbrace r_{\rm{BHL}},r_{\rm{Hill}}\right\rbrace\), where \(r_{\rm{BHL}}\simeq G m_{\rm{bin}}/(v_{\rm{rel}}^{2}+c_{\rm{s,AGN}}^{2})\) is the BHL radius, and \(r_{\rm{Hill}}=(m_{\rm{bin}}/3M)^{1/3}R\) is the Hill radius, or is approximated to \(0.6H\) [54], where \(H\) denotes the vertical scale height of the disk. We estimate the timescale of a kicked remnant crossing the cavity as \[t_{\rm{kick}}=r_{\rm{cav}}/v_{\rm{k}}\simeq 37~days \left(\frac{r_{\rm{cav}}}{10^{14}\text{ cm}}\right) \left(\frac{v_{\rm{k}}}{10^{7.5}\text{ cm}\text{ s}^{-1}}\right)^{-1}.\] As shown in Figure 1, \(t_{\rm{kick}}\) increases with the binary location \(R\), which would enlarge the time delay between a BH merger and its associated EM emission, since the BH needs to interact with the dense AGN disk gas to efficiently release energy (see below). However, given the uncertain existence and size of a cavity surrounding the merging BBH, we assume that the remnant is directly kicked into the AGN disk environment, and discuss the potential time delay caused by cavity in Section 4.4.
3 Interaction between kicked remnant and AGN disk environment — jet and cocoon↩︎
3.1 Formation and power of BH-driven jet↩︎
After the embedded BBH merger, the kicked remnant moving through the AGN disk with \(v_{\rm{k}}\) would accrete the ambient gas with a mass inflow rate \(\dot{M}_{\rm{BHL,k}}\), \[\dot{M}_{\rm{BHL,k}}=\frac{4 \pi G^2 m_{\rm{bin}}^2 \rho_{\rm{AGN}}}{(v_{\rm{k}}^{2}+c_{\rm{s,AGN}}^{2} )^{3/2}} \simeq1.6 \times 10^7 \dot{M}_{\rm{Edd}} \left(\frac{m_{\rm{bin}}}{100 M_\odot}\right) \left(\frac{\rho_{\rm{AGN}}}{10^{-10}\,{\rm g\,cm^{-3}}}\right) \left(\frac{v_{\rm{k}}}{10^{7}\,{\text{ cm}\text{ s}^{-1}}}\right)^{-3}.\] where in the second equality, only \(v_{\rm{k}}\) is considered for an intuitive order of magnitude estimation, while in the subsequent specific calculation of \(\dot{M}_{\rm{BHL,k}}\), both \(v_{\rm{k}}\) and \(c_{\rm{s,AGN}}\) are taken into account. The hyper-Eddington accretion is realizable, since for BHL accretion, the inflow is highly quasi-spherical El?, Mellah15? and the released gravitational energy is advected inward with gas [62]. Meanwhile, the AGN disk would be magnetized, of which the ratio of ambient gas to magnetic pressure \(\beta \lesssim 10-100\) [63]–[65]. Recent numerical simulations indicate that the ambient magnetic fields are frozen and flow inward with gas, resulting in their accumulation to saturation near the BH [65], [66]. Due to a large spin of the merger remnant [67], [68], a jet would be generated via the Blandford-Znajek (BZ) mechanism [69], of which the power can be estimated as \[L_{\rm{jet}}=f \dot{M}_{\rm{BHL,k}} c^2,\] where \(f \sim 0.1\) for \(\beta \lesssim 10-100\) (according to Figure 3 in [65]), containing effects of both the jet efficiency and the reduction of accretion rate.
As shown in Figure 2, overall, the power of the BH-driven jet surpasses the bolometric luminosity of AGN disks, \(L_{\rm{bol,AGN}}\), across an extensive range of \(R\), thereby rendering the jet potentially observable for efficient specific radiation processes. Some cases possess weak jets with \(L_{\rm{jet}}<L_{\rm{bol,AGN}}\), thus unfavorable for observations, e.g., the \(v_{\rm{k}} = 10^{3}\rm{~km~s}^{-1}\) and \(m_{\rm{bin}}=10\rm{M}_{\odot}\) case due to a lower \(\dot{M}_{\rm{BHL,k}}\), and the \(\rm{TQM}\) case due to a lower disk density compared with the SG model. Also, we reduce \(f\) to \(0.01\) on account of the captured AGN disk gas likely carrying non-negligible angular momentum, which would potentially reduce the mass rate accreted onto BH, and find that though contracted, there is still a range of \(R\) for \(L_{\rm{jet}}>L_{\rm{bol,AGN}}\).
In addition, since the embedded BBH would undergo binary-single interaction to alter its direction of orbital angular momentum [16], [26], [70], and given that the direction of GW kick strongly relies on spin orientations [56], \(\vec{v}_{\rm{k}}\) may be randomized. Consequently, the minimum timescale for a merger remnant to exit the AGN disk is estimated as \(t_{\rm{k}}=H/v_{\rm{k}}\). Meanwhile, the jet formation requires at least a few accretion timescales \(t_{\rm{BHL}}\simeq r_{\rm{BHL}}/v_{\rm{k}} \sim G m_{\rm{bin}}/v_{\rm{k}}^3\) [65]. So the merger remnant is more feasible to launch jet within AGN disk when \(t_{\rm{BHL}}<t_{\rm{k}}\), which holds over large \(R\) regions, as shown in Figure 2.
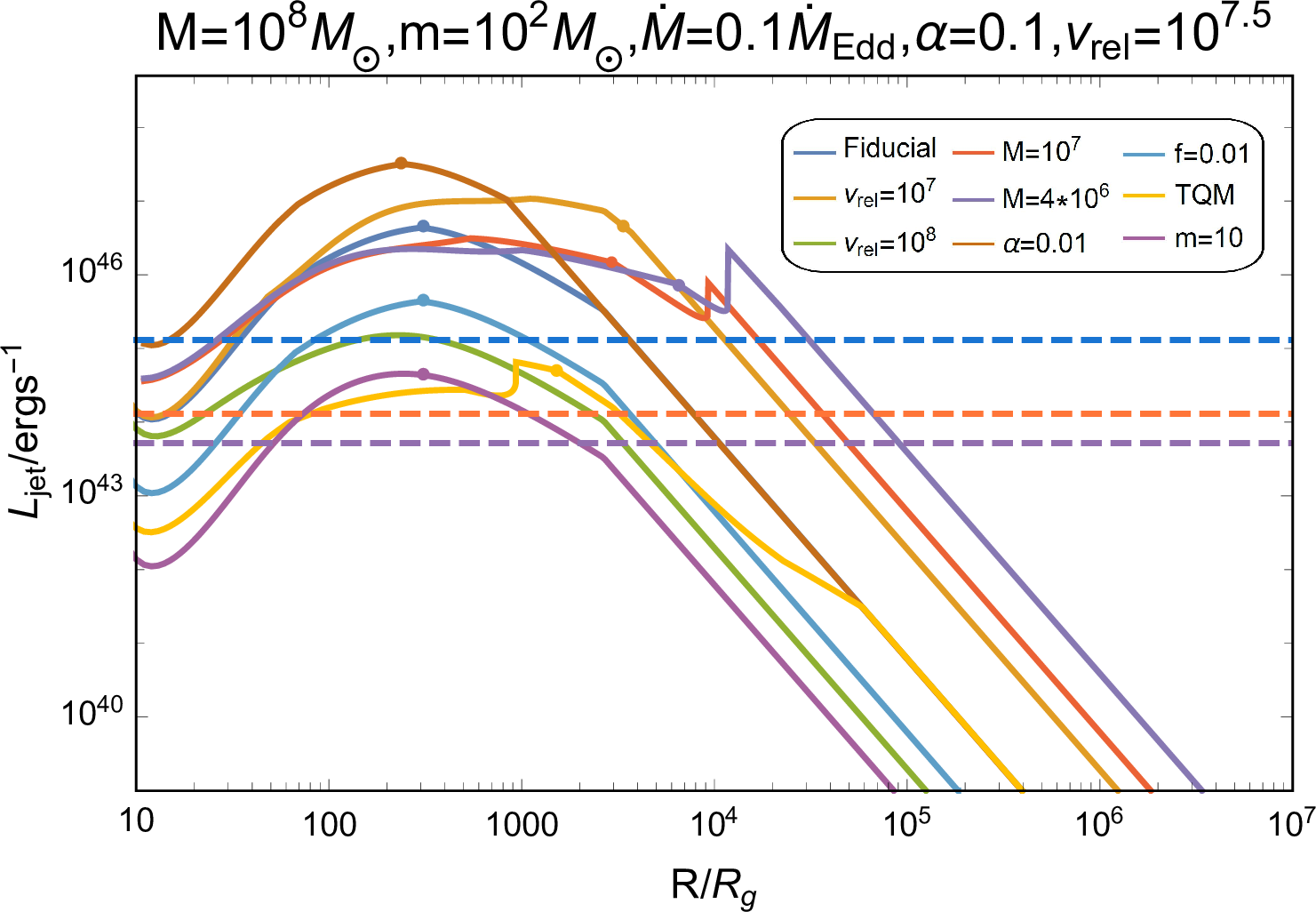
Figure 2: Power of a jet launched by a kicked merger remnant moving through the magnetized AGN disk environment with different system parameters (the inset shows these parameters). The blue, orange, and purple dashed lines represent the bolometric luminosity of AGN disk \(L_{\rm{bol,AGN}}=0.1 \dot{M} c^2\) with \(M=10^{8}, 10^{7}, 4\times10^{6}~\rm{M}_{\odot}\), respectively. The point laid on each curve represents \(t_{\rm{BHL}}=t_{\rm{k}}\) with the right side \(t_{\rm{BHL}}<t_{\rm{k}}\).
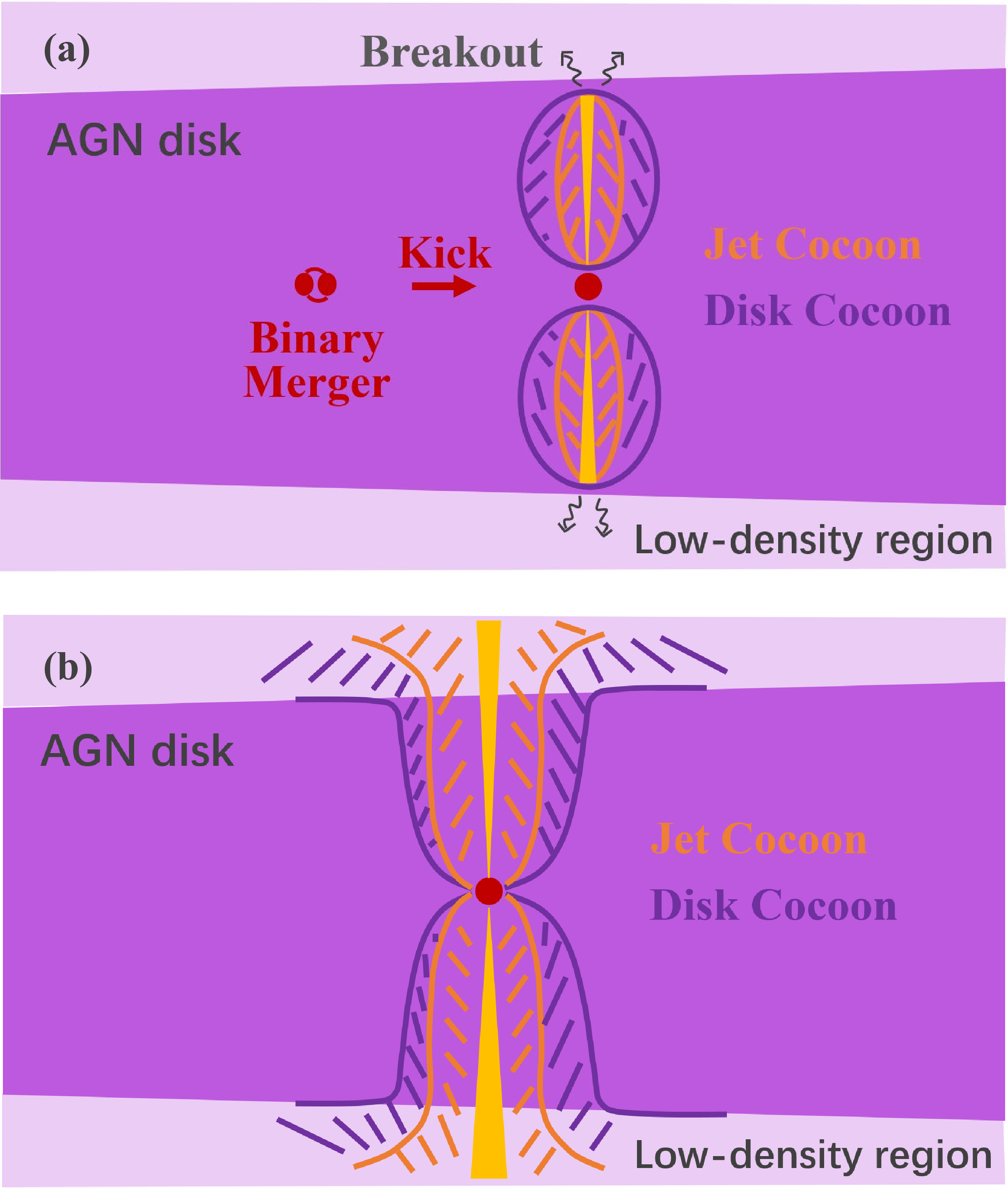
Figure 3: Schematic diagram illustrating the evolution of a jet and a cocoon driven by a kicked BBH merger remnant traversing the AGN disk. (a) The kicked remnant accretes ambient magnetized gas and launches a jet, which propagates through and interacts with the AGN disk to generate a two-component cocoon; at the jet breakout, photons can diffuse out from the jet head to produce emission. (b) After the jet breakout, the jet cocoon and disk cocoon severally expands, cools, and produces emission.
3.2 Propagation and breakout of a jet within the AGN disk↩︎
We consider a representative scenario where a BBH merger occurs at the midplane of the AGN disk, and the remnant is kicked along the disk plane. Additionally, we assume that a jet driven by the BZ mechanism propagates vertically to the disk plane. A schematic diagram illustrating the evolution of a kicked BH and its associated jet is depicted in Figure 3. The jet interacts with the dense ambient medium during its propagation, forming a shocked structure at its head position and a lateral hot cocoon, which would in turn collimate the jet e.g. [71], [72]–[74]. The jet is initially Poynting flux dominated, but would behave as a baryon dominant one at large scale due to the early dissipation of magnetic fields [75]–[77]. For simplicity, therefore, we consider a hydrodynamic jet and investigate its propagation through the AGN disk.
We calculate the evolution of the jet and cocoon following the descriptions in [74]. Collision of the jet with the ambient AGN disk gas at its head generates a forward shock and a reverse shock, where the ram pressure balance sets the velocity of jet head as \[\label{vh} \beta_{\rm{h}}=\frac{\beta_{\rm{j}}}{1+\tilde{L}^{-1/2}},\tag{1}\] where the jet velocity \(\beta_{\rm{j}} \sim 1\), and the collimation parameter is \[\label{Lcol} \tilde{L}\equiv\frac{\rho_{\rm{j}} h_{\rm{j}}\Gamma_{\rm{j}}^2}{\rho_{\rm{AGN}}}\simeq\frac{L_{\rm{jet}}}{\Sigma_{\rm{j}}\rho_{\rm{AGN}}c^3},\tag{2}\] where \(\rho_{\rm{j}}\), \(h_{\rm{j}}\) and \(\Gamma_{\rm{j}}\) are density, specific enthalpy and Lorentz factor of the jet; the second equation holds as the total jet energy density \(\rho_{\rm{j}}h_{\rm{j}}\Gamma_{\rm{j}}^2-\rho_{\rm{j}}\Gamma_{\rm{j}}-p_{\rm{j}} \sim \rho_{\rm{j}}h_{\rm{j}}\Gamma_{\rm{j}}^2 =L_{\rm{jet}}/\Sigma_{\rm{j}}c^3\) [72], where \(p_{\rm{j}}\) and \(\Sigma_{\rm{j}}\) are pressure and cross-section of the jet. The gas flowing into the jet head through the shocks would then flows laterally to the cocoon, transferring energy from the head. Assuming the radiation loss is negligible since the AGN disk is highly opaque (see Appendix 7), the energy deposited into the cocoon is \(E_{\rm{c}} \simeq L_{\rm{jet}}(t-z_{\rm{h}}/c)\), where \(t\) is the duration of the jet propagation and \(z_{\rm{h}}= \beta_{\rm{h}} c t\) is the height of the jet head. Besides, a high \(\beta_{\rm{h}}\) would cause the shock and the energy flux being radiation dominated [78], so the cocoon’s pressure can be estimated as \[\label{Pc} P_{\rm{c}}=\frac{E_{\rm{c}}}{3V_{\rm{c}}}\simeq\frac{L_{\rm{jet}}(1-\beta_{\rm{h}})}{3\pi c^3\beta_{\rm{h}}\beta_{\rm{c}}^2t^2},\tag{3}\] where the cocoon is set as a cylinder with height \(z_{\rm{h}}\) and radius \(r_{\rm{c}}=\beta_{\rm{c}}t\), of which \(\beta_{\rm{c}} \sim \sqrt{P_{\rm{c}}/(\rho_{\rm{AGN}}c^2)}\) is its lateral expansion velocity. For a high \(P_{\rm{c}}\), the cocoon would collimate the jet, of which the cross-section is constrained to \[\label{sigma} \Sigma_{\rm{j}}\simeq\frac{L_{\rm{jet}}\theta_0^2}{4cP_{\rm{c}}},\tag{4}\] where \(\theta_0\) is the initial opening angle of the jet, which is set by a fiducial value of \(0.17 ~(10^\circ)\). Combining Equation (1 )-(4 ), \(\tilde{L}\) can be expressed by \[\label{Lcol2} \tilde{L} = \left(\frac{L_{\rm{jet}}}{\rho_{\rm{AGN}}t^2\theta_0^4c^5}\right)^{2/5}.\tag{5}\]
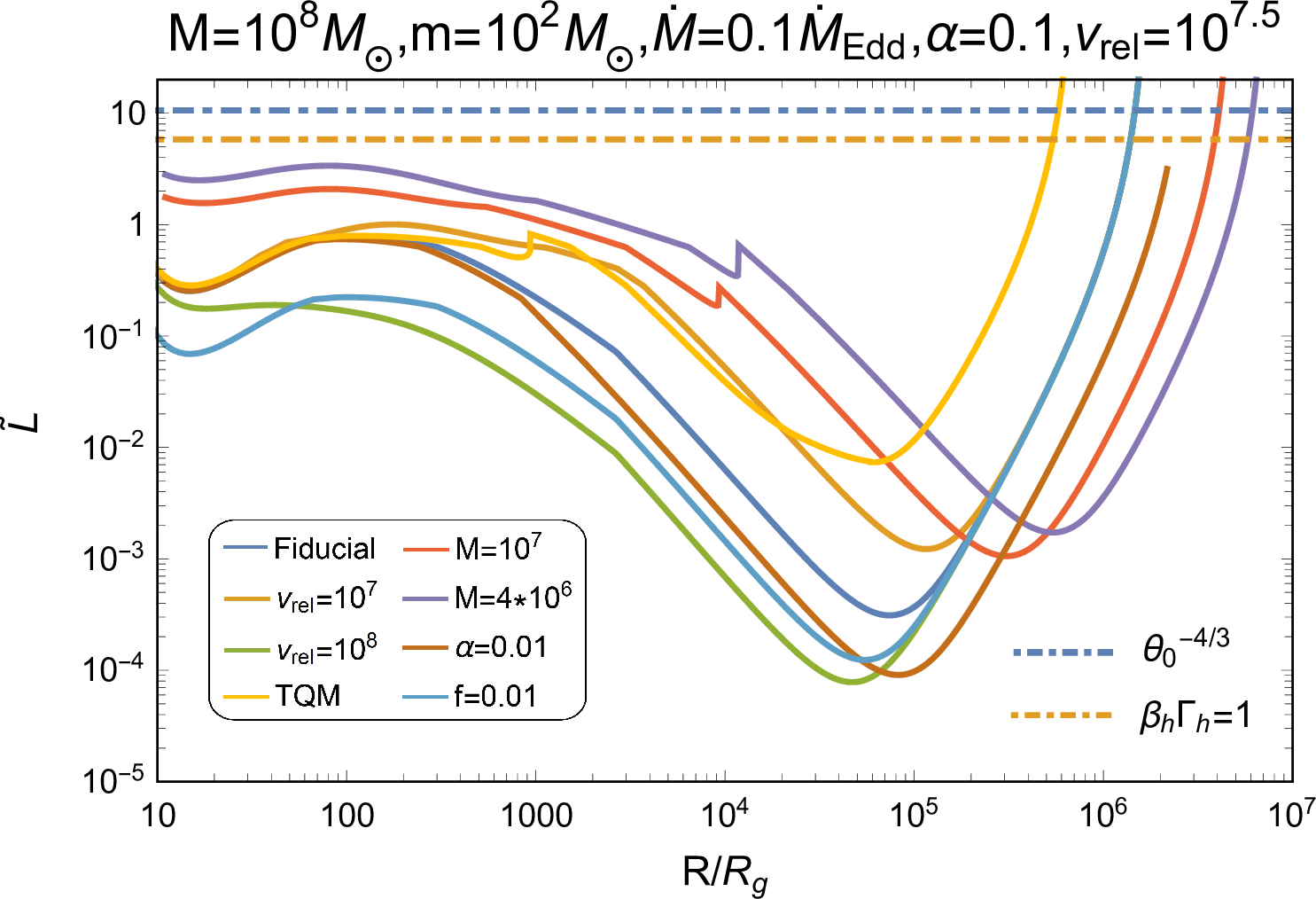
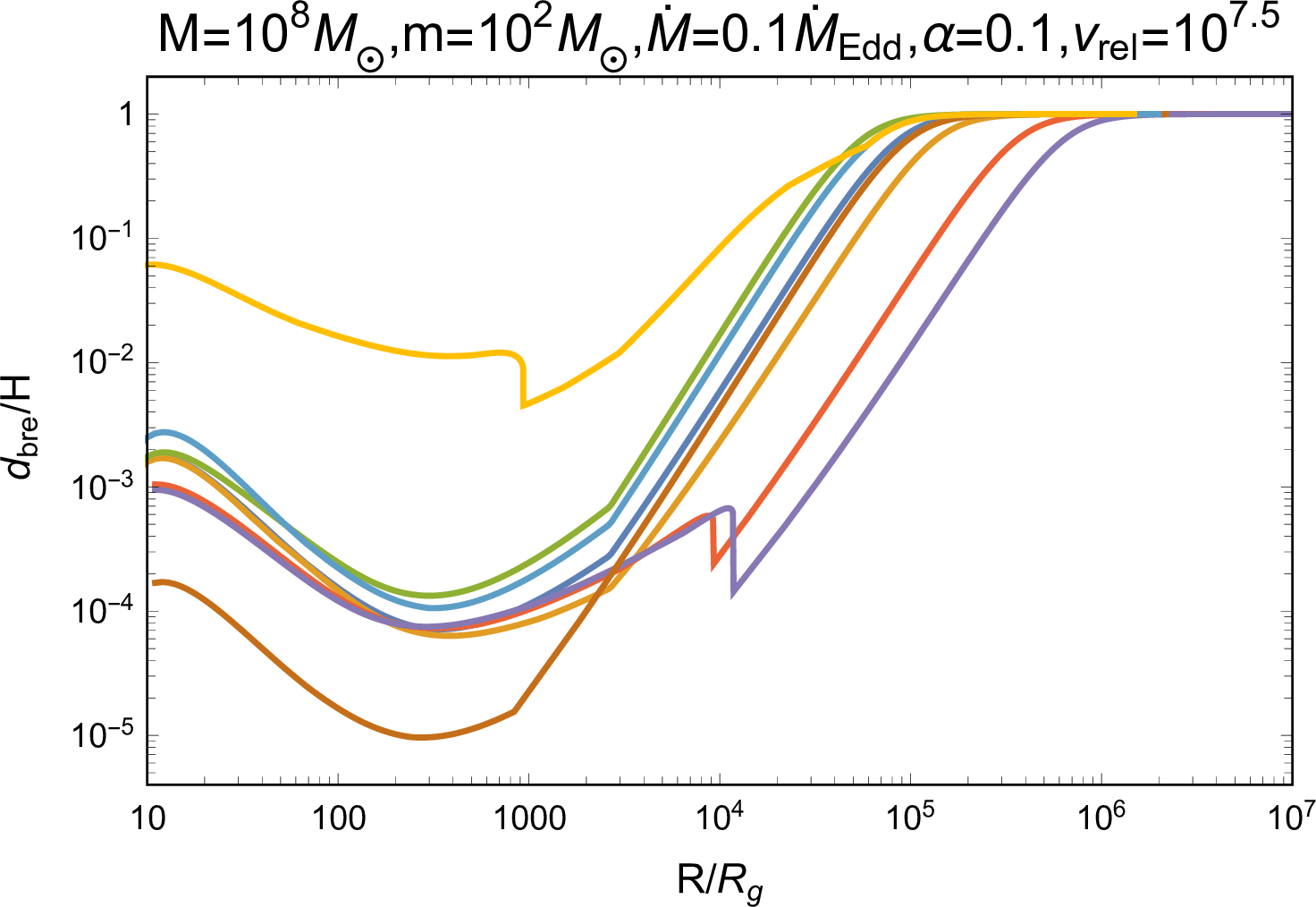
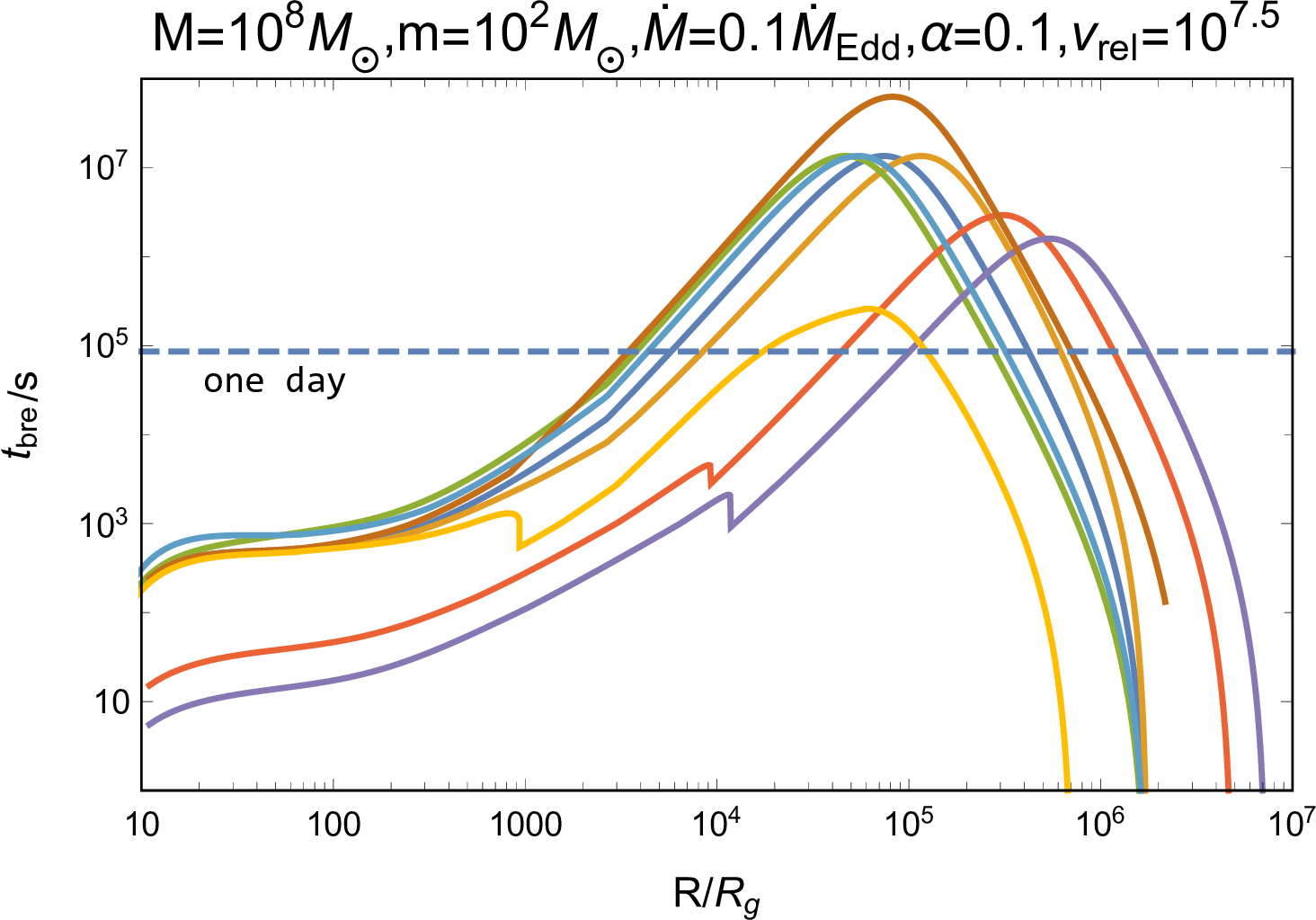
Figure 4: Various properties of the jet at its breakout, consisting of the jet collimation parameter \(\tilde{L}\), the thickness between the jet head and the AGN disk surface \(d_{\rm{bre}}\), and the time of jet propagation before the breakout \(t_{\rm{bre}}\). The blue and orange dot-dash lines in the \(\tilde{L}\) panel severally represents the criterion of collimation, of which the jet is uncollimated when \(\tilde{L}>\theta_0^{-4/3}\) [74], and the head’s motion being relativistic. The blue dashed line in the \(t_{\rm{bre}}\) panel represents the time equaling to one day..
As the jet approaches the AGN disk surface, photons behind the shock would diffuse faster than the jet head propagation, leading to the shock breakout. We set the distance between the jet head and the disk surface at breakout as \(d_{\rm{bre}}\), where the photon diffusion time, \(t_{\rm{diff,h}}\sim d_{\rm{bre}}^2\kappa_{\rm{AGN}}\rho_{\rm{AGN}}/c\), equals to the head dynamical timescale \(t_{\rm{dyn}}\sim d_{\rm{bre}}/\beta_{\rm{h}}c\), i.e., \[\label{dbre} d_{\rm{bre}}=\frac{1}{\kappa_{\rm{AGN}}\rho_{\rm{AGN}}\beta_{\rm{h}}},\tag{6}\] where we assume \(\kappa_{\rm{AGN}}=0.34\text{ cm}^2\text{ g}^{-1}\) for the Thompson scattering of ionized gas (a detailed discussion is shown in Appendix 7). We calculate \(\tilde{L}\) (i.e. \(\beta_{\rm{h}}\)) at the time of breakout \(t_{\rm{bre}}=(H-d_{\rm{bre}})/\beta_{\rm{h}}c\) via Equation (1 ), (5 ) and (6 ), where we ignore the case of the AGN disk being initially optically thin, i.e., \(\kappa_{\rm{AGN}}\rho_{\rm{AGN}} H<1\); the results are shown in Figure 4. First, for various system parameters, almost all jets are Newtonian and possess \(\tilde{L}<\theta_0^{-4/3}\), thereby are collimated by cocoons [74]; also, the head velocities are large enough to generate radiation-dominated shocks [78]. So, our calculations under the premise of collimation and radiation-domination are valid. Second, except for the outer AGN disk regions, the thickness \(d_{\rm{bre}}\ll H\), indicating that the jets adequately interact with the environment and the radiation just starts to escape near the disk surface. Conversely, in regions with large \(R\), the diffusion of photons from the shock at early stage can significantly impact the propagation of jets; fortunately, the jet’s power is weak at these radii, as shown in Figure 2, allowing us to disregard the resulting inaccuracies. Third, the values of \(t_{\rm{bre}}\) are distributed over a large range, depending mainly on the properties of AGN disk rather than the kick velocity \(v_{\rm{k}}\) and the feedback efficiency \(f\).
In addition, we can derive the cocoon’s properties at the jet breakout, i.e., the total energy in the cocoon \[\label{Ec} E_{\rm{c}} \simeq L_{\rm{jet}} t_{\rm{bre}} (1-\beta_{\rm{h}}(t_{\rm{bre}})),\tag{7}\] and the volume of the cocoon \[\label{Vc} V_{\rm{c}} \simeq \pi \beta_{\rm{h}}(t_{\rm{bre}}) \beta_{\rm{c}}(t_{\rm{bre}})^2 c^3 t_{\rm{bre}}^3.\tag{8}\] At the jet breakout, radiation losses at the head shock come into play, impeding effective energy transfer to the cocoon. Subsequently, the cocoon undergoes independent evolution driven by its initial energy and volume of Equation (7 ) and (8 ).
4 EM emission powered by a kicked remnant-driven jet↩︎
During the jet breakout phase with \(t_{\rm{diff,h}}<t_{\rm{dyn}}\), photons would escape from the head shock, thereby having the potential to produce detectable emission. Besides, during the propagation within the AGN disk, the jet deposits a huge amount of energy to the cocoon, which would thus be a competent emission source as well. The cocoon comprises two components (see panel (a) of Figure 3): the so-called disk and jet cocoon, composed of the AGN disk medium and the jet material crossing the head’s shock, respectively, separated by a contact discontinuity [74]. Both components are expected to generate emission during their expansion following breakout (see panel (b) of Figure 3).
Therefore, in what follows, we investigate the emission during jet breakout, as well as the cooling emission from both disk cocoon and jet cocoon, focusing on the observed properties, comprising luminosity, duration, and temperature, of the emission.
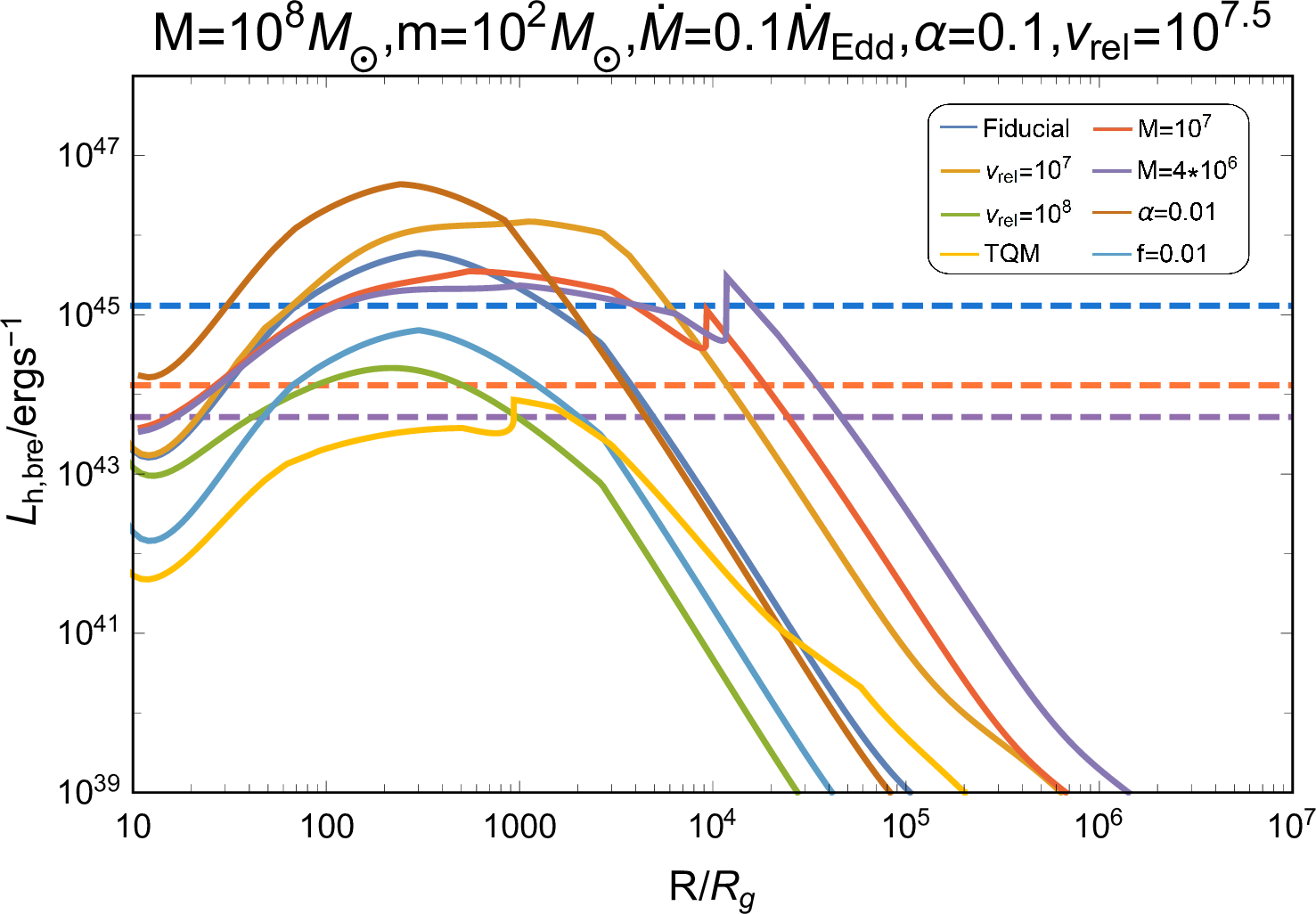
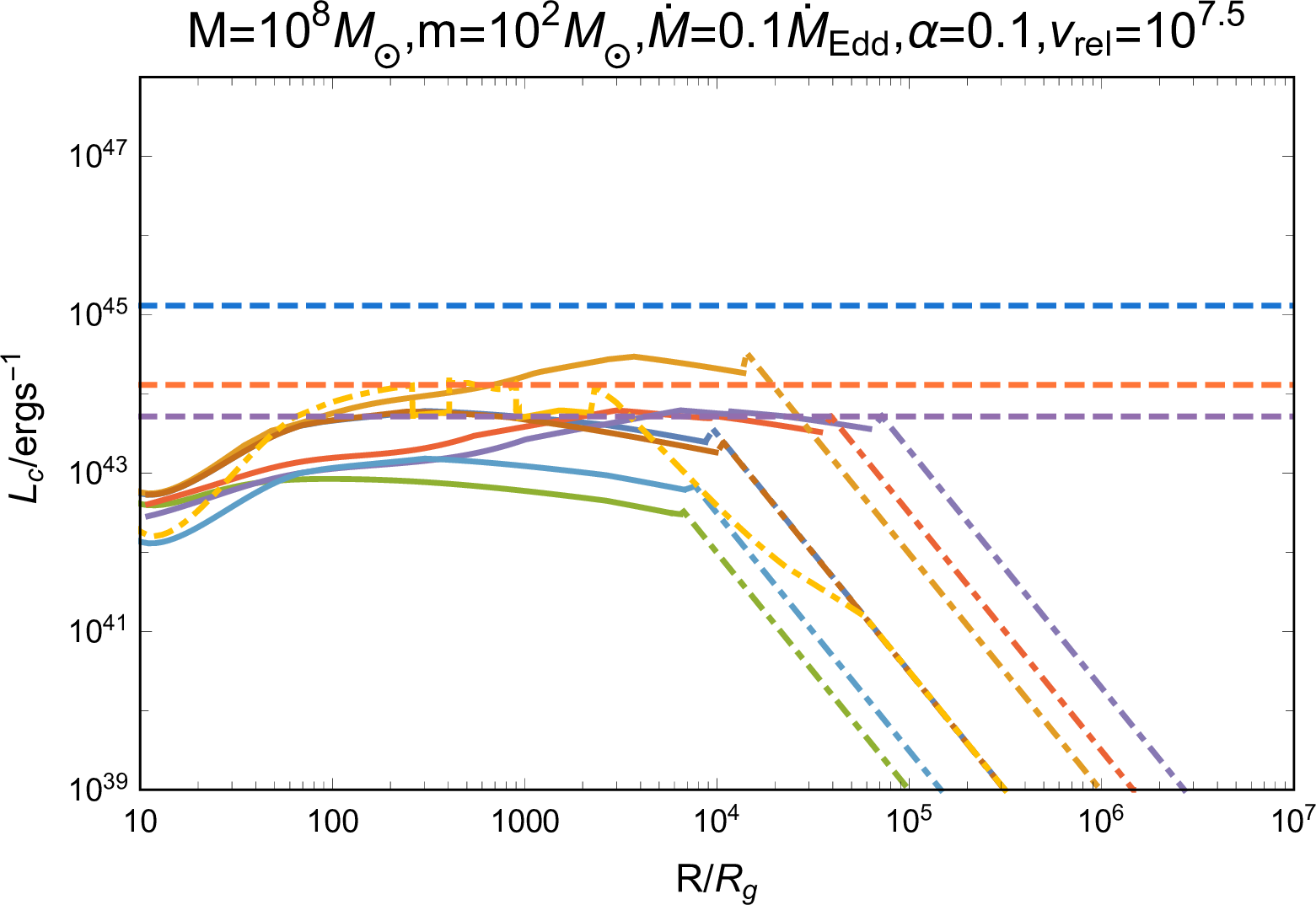

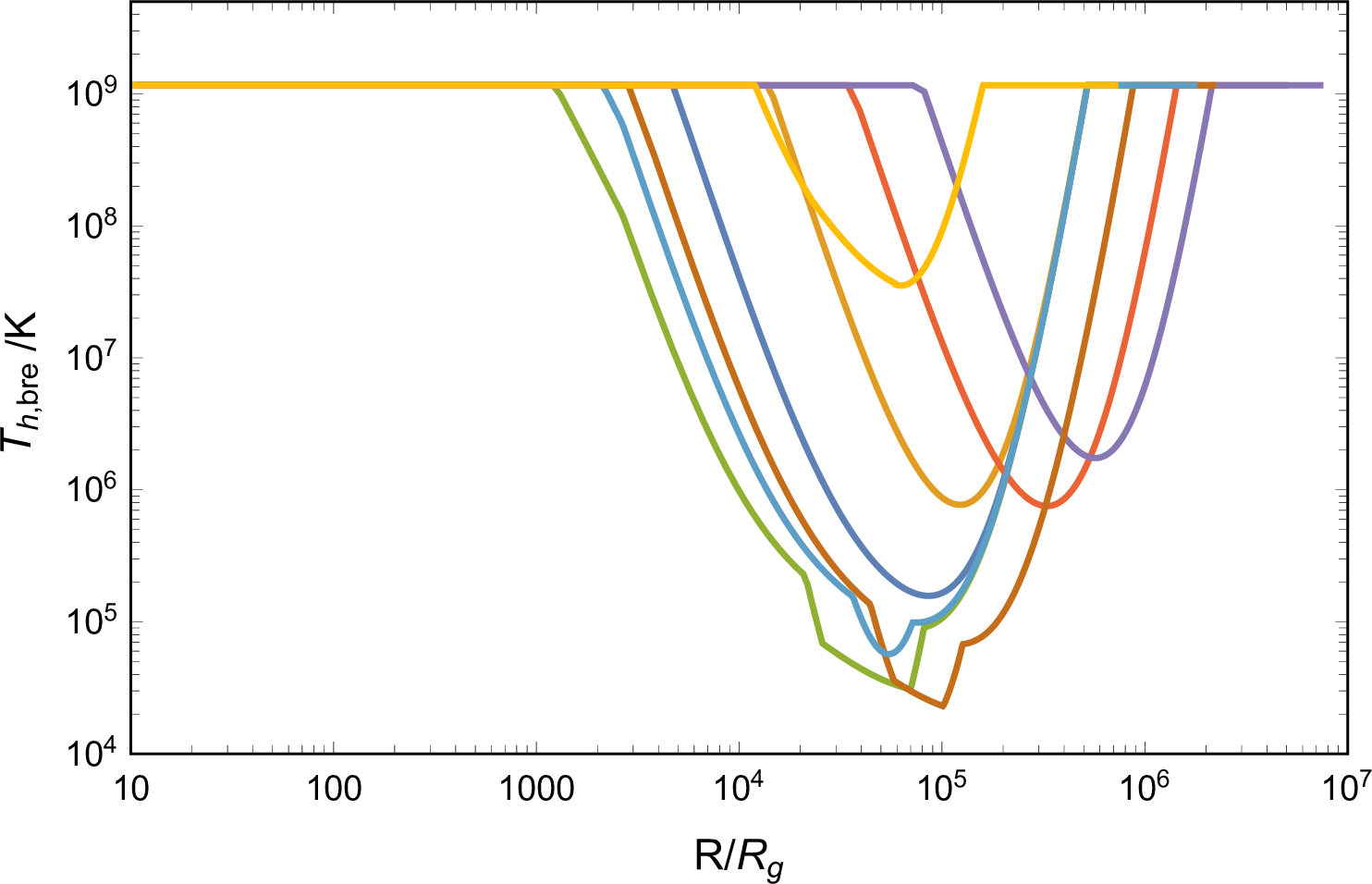
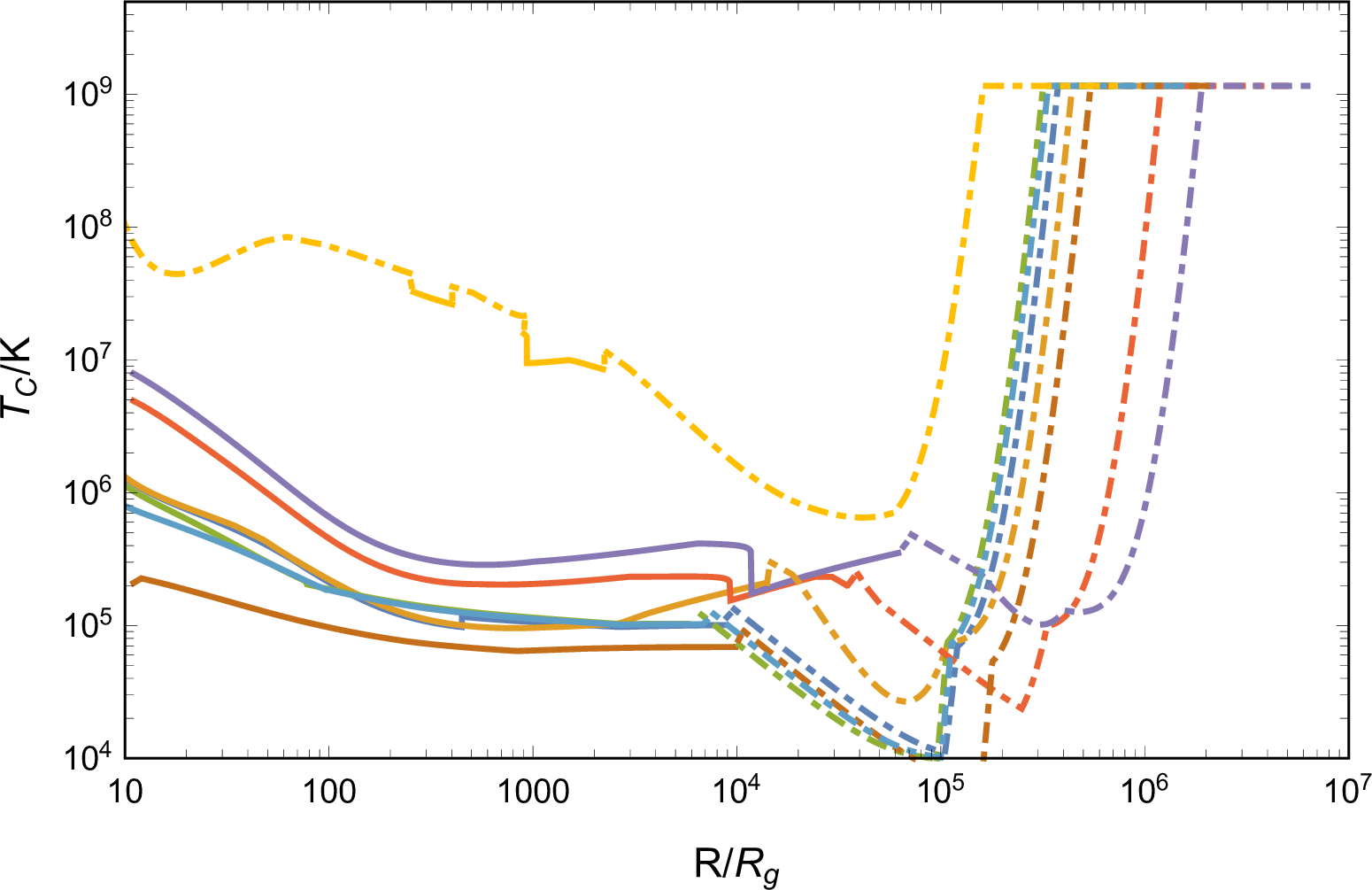
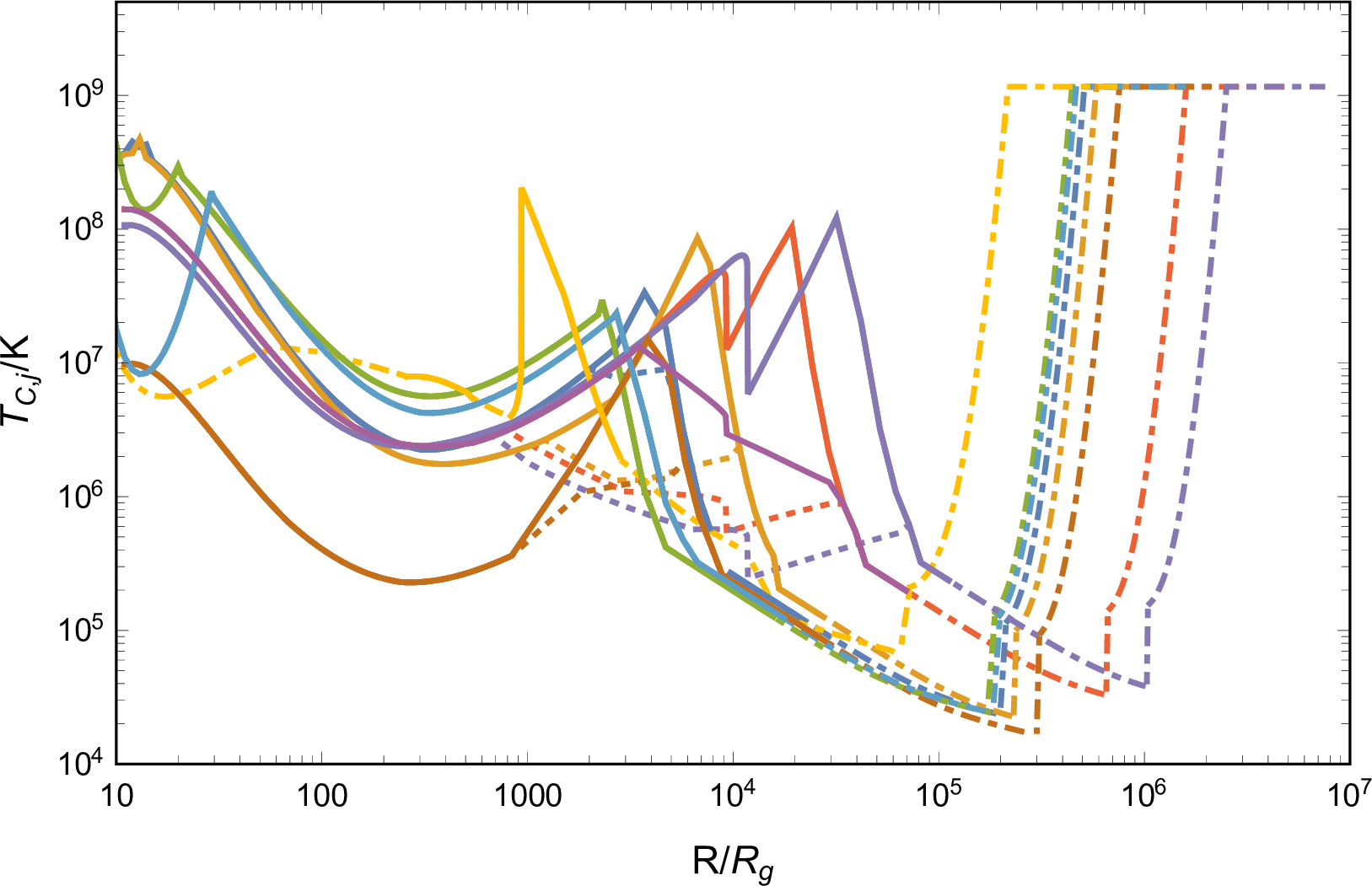
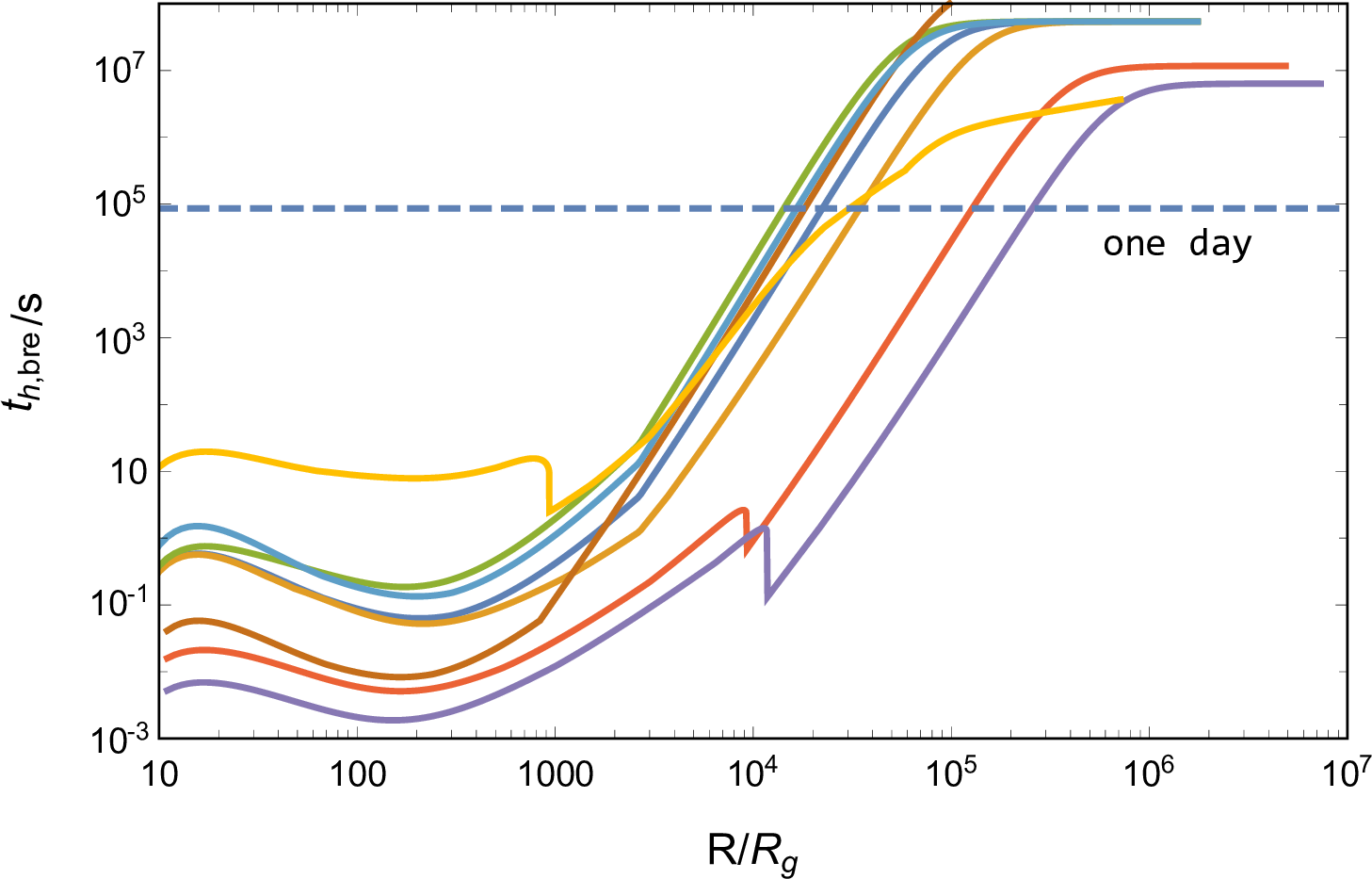
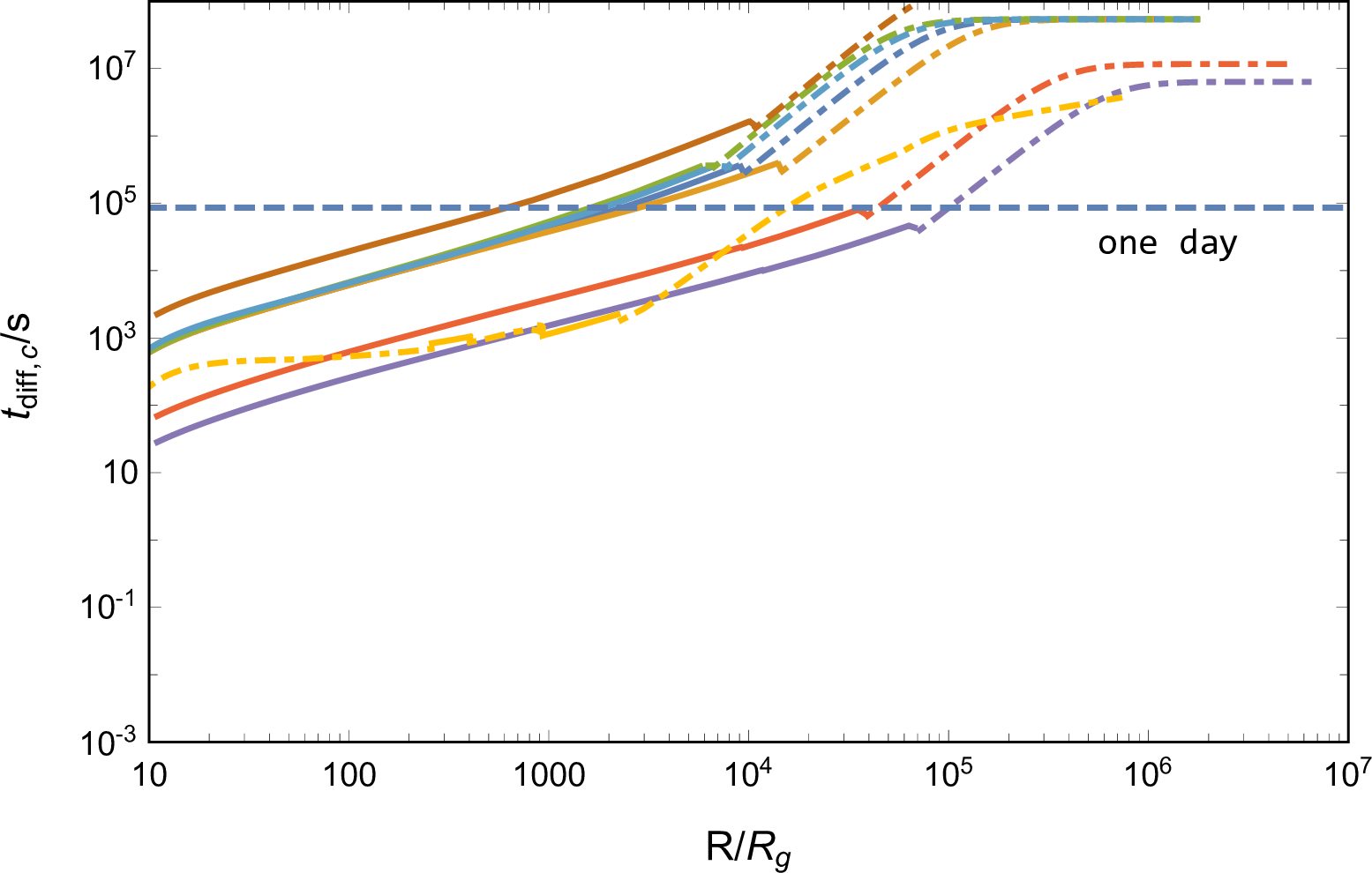
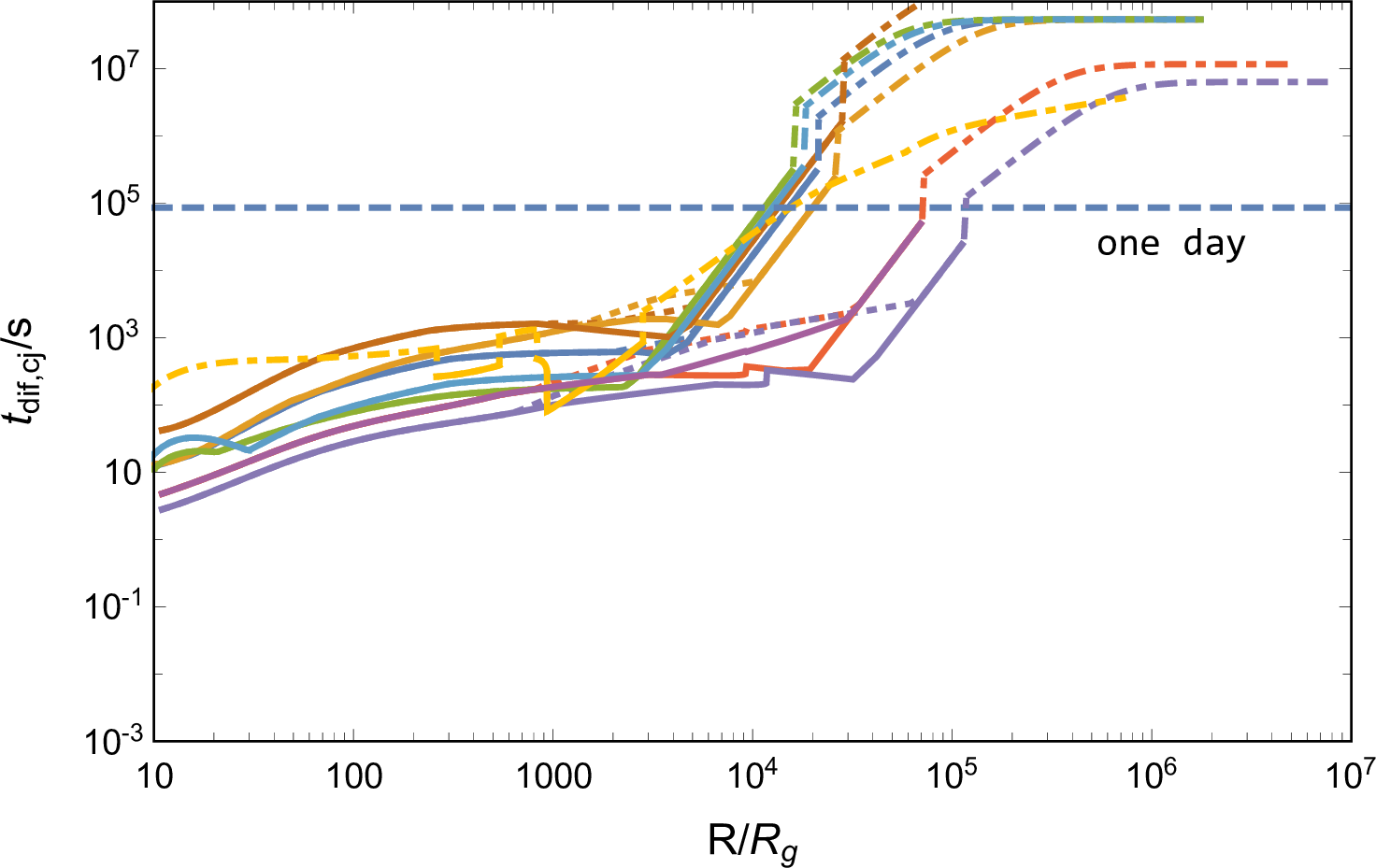
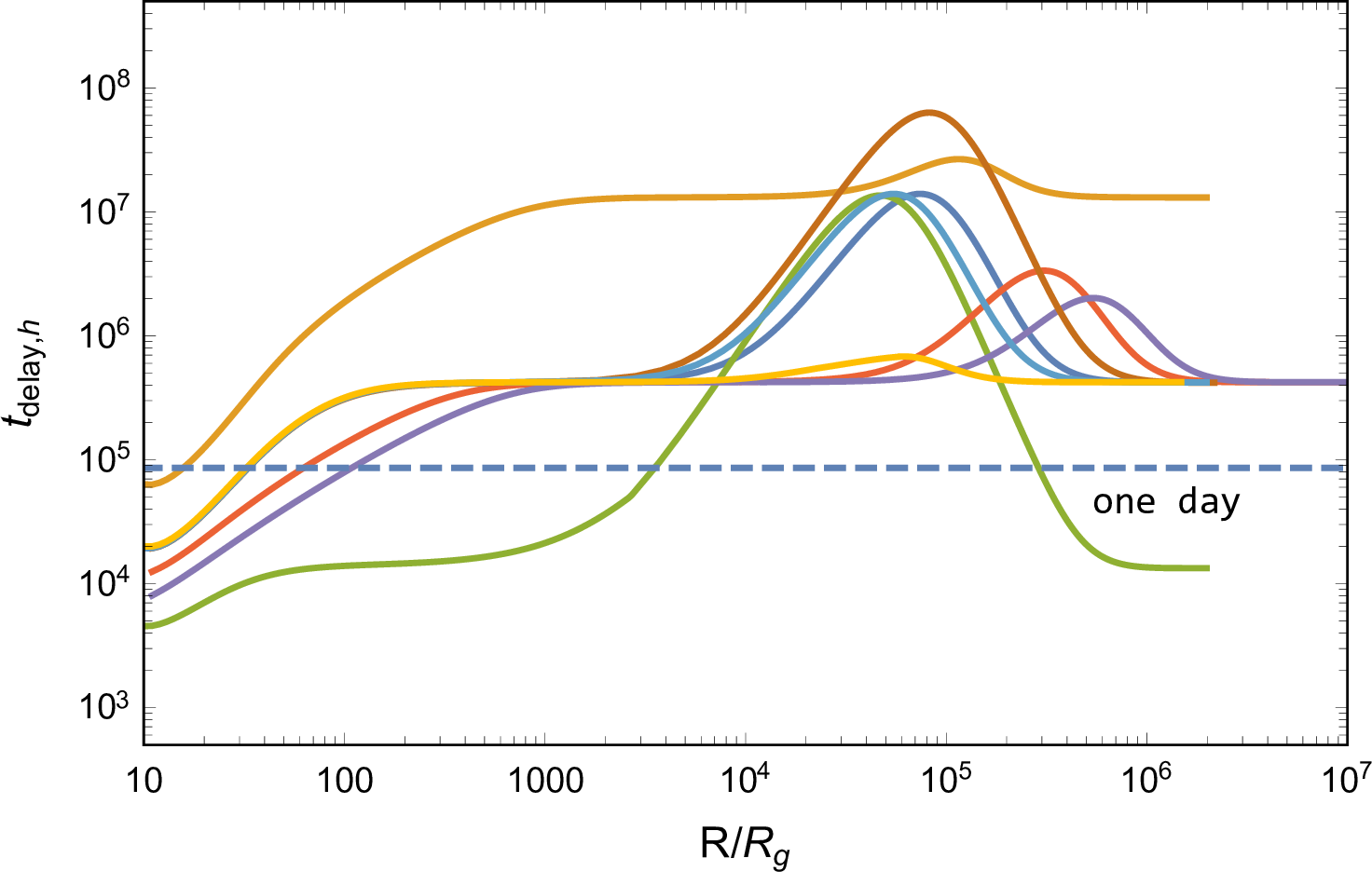
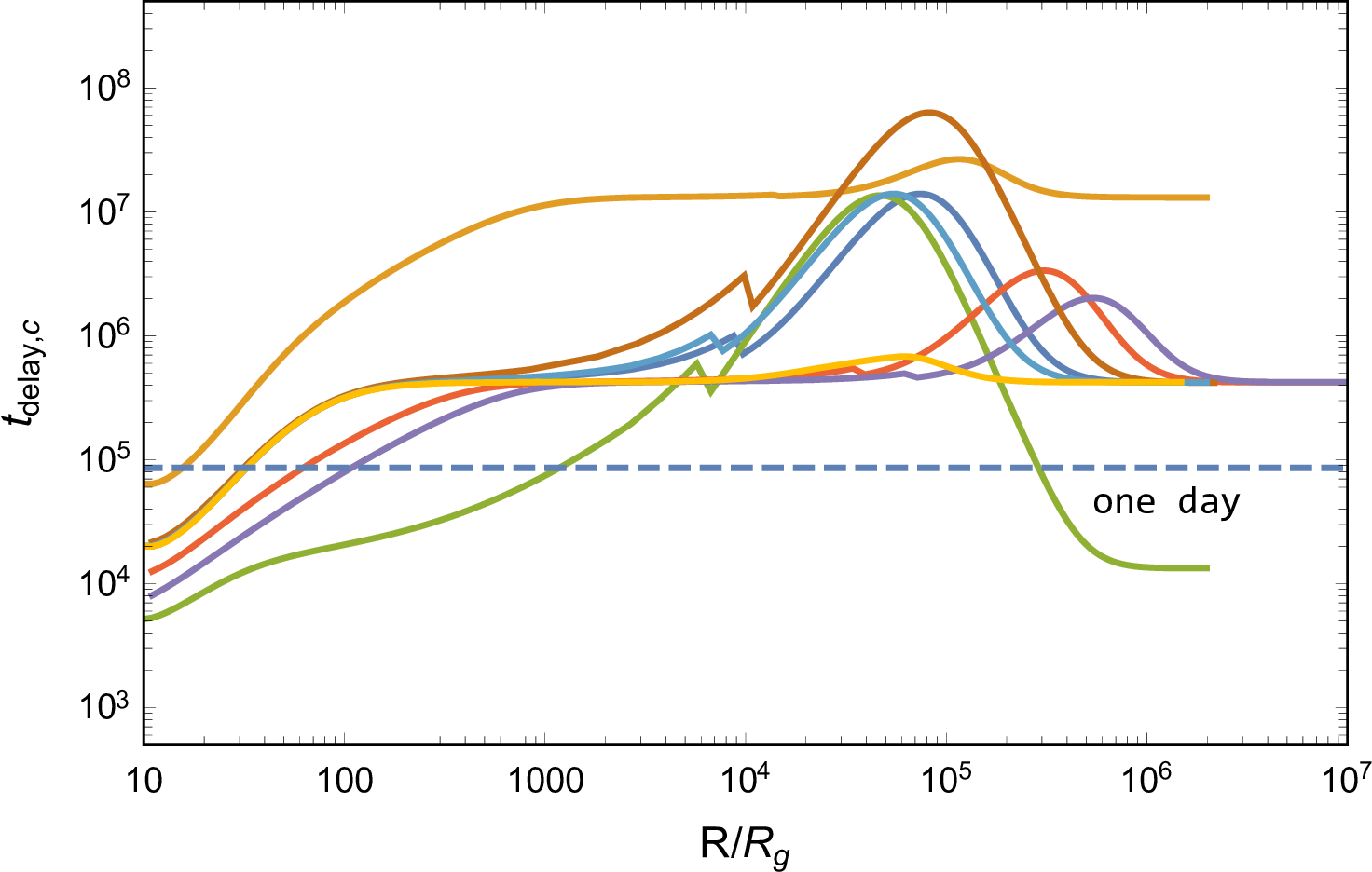
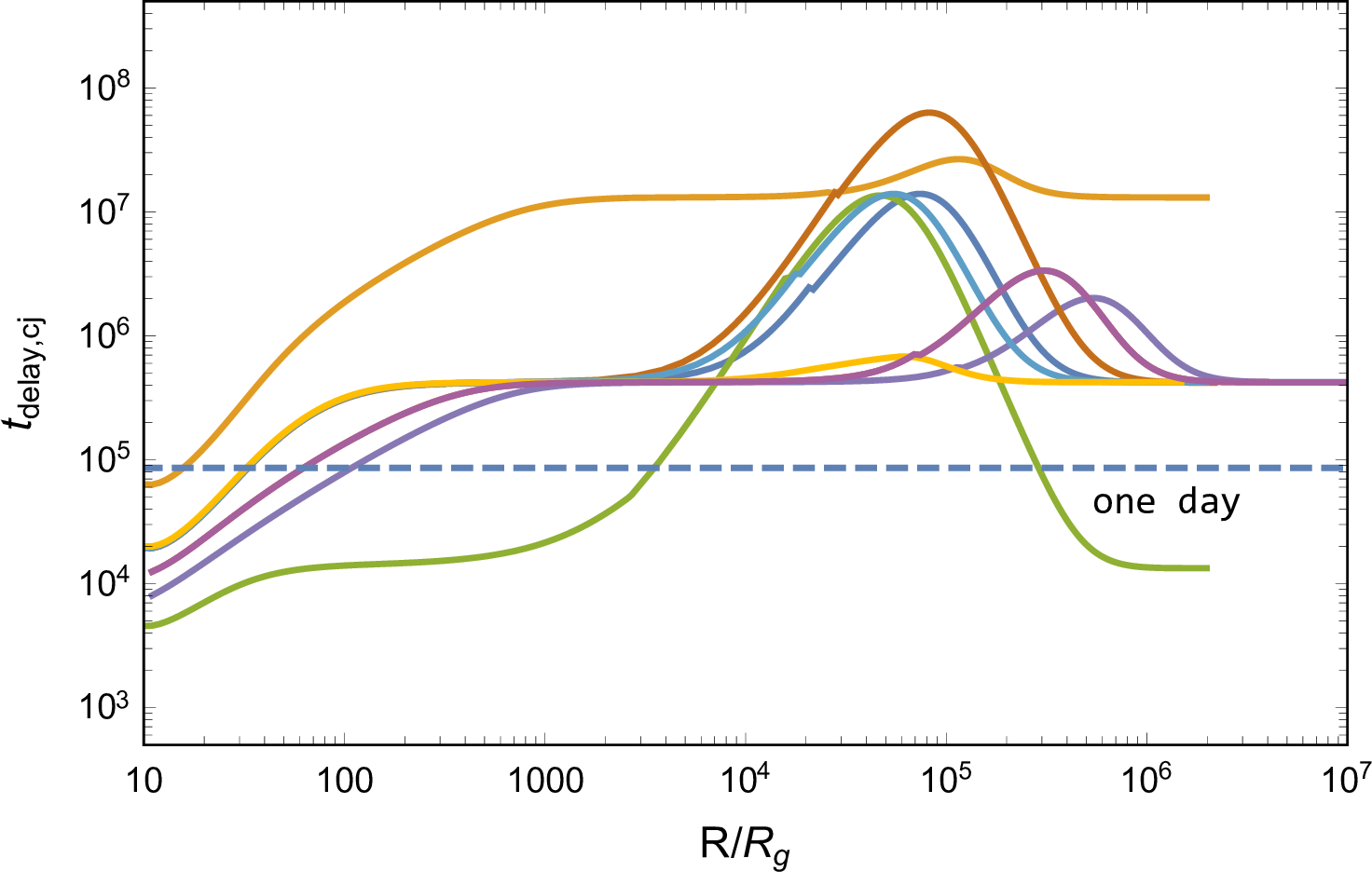
Figure 5: Observed properties of the emission during jet breakout (the first column), from cooling disk cocoon (the second column), and cooling jet cocoon (the third column), including luminosity, temperature, duration timescale, and time delay. The blue, orange, and purple dashed lines in the first row represent the bolometric luminosity of the AGN disk \(L_{\rm{bol,AGN}}=0.1 \dot{M} c^2\). The blue dashed lines in the third and forth row represent the time equaling to one day. The dot dash lines in the second and third columns show the \(R\) regions where photons can escape from the cocoons before the jet breakout, and thereby the jet evolution is inaccurate. In addition, in panels of \(T_{\rm{cj}}\) and \(t_{\rm{diff,cj}}\), the dotted lines represent the properties of emission with \(L_{\rm{cj}}=L_{\rm{bol,AGN}}\), i.e., nearly equaling to the AGN disk background radiation. In the third column we additionally consider the case with parameters \(M=10^{7}\rm{M}_{\odot}\) and \(\beta_{\rm{cj}}=5v_{\rm{c}}/c\), indicating the cooling emission of a jet cocoon, which is specifically mixed with the disk cocoon..
4.1 Emission during jet breakout↩︎
During jet breakout, the head continuously shocks the AGN disk medium, but at the moment, photons behind the radiation-dominant shock can diffuse out and take away most of the energy. Thus, the luminosity of the emission can be estimated as [37] \[L_{\rm{h,bre}} \simeq \Sigma_{\rm{j}} \rho_{\rm{AGN}} \beta_{\rm{h}}^3 c^3,\] and the duration can be estimated as the diffusion timescale, \[t_{\rm{h,bre}} \simeq t_{\rm{diff,h}} = \frac{1}{\kappa_{\rm{AGN}}\rho_{\rm{AGN}}\beta_{\rm{h}}^2c}.\]
We focus on the thermal emission. The thermal equilibrium temperature behind the shock can be calculated via the jumping condition for gas with the adiabatic index \(\gamma=4/3\) [79], i.e., \[T_{\rm{BB,hbre}} = \left(\frac{18}{7a}\rho_{\rm{AGN}}\beta_{\rm{h}}^2c^2\right)^{0.25},\] where \(a\) is the radiation constant. However, because the jet head’s velocity is high, as shown in Figure 4, radiation behind the shock may deviate from thermal equilibrium if an insufficient number of photons are generated by gas via free-free emission. In such a case, the shock would attain a thermal Compton equilibrium at temperature \(>T_{\rm{BB,hbre}}\). Moreover, for even higher temperatures, pair production processes will be invoked to restrict the temperature [80]–[83].
To determine the radiation temperature, we employ the methodology described in [82]. A thermal coupling coefficient can be utilized as an indicator of thermal equilibrium, i.e., \[\eta \equiv \frac{n_{\rm{BB}}\left(T_{\rm{BB,hbre}}\right)}{t_{\rm{h,bre}} \dot{n}_{\rm{ph},\rm{ff}}\left(T_{\rm{BB,hbre}}\right)},\] where \(n_{\rm{BB}}\sim aT_{\rm{BB}}^4/3kT_{\rm{BB}}\) is the photon number density required for thermal equilibrium, \(k\) is the Boltzmann constant, and \(\dot{n}_{\rm{ph},\rm{ff}} \approx 3.5\times 10^{36}\text{ s}^{-1}\text{ cm}^{-3} \rho_{\rm{AGN}}^2 T^{-1/2}\). For \(\eta<1\), the radiation can achieve thermal equilibrium with temperature \(T_{\rm{BB,hbre}}\). For \(\eta>1\), photons are starved to reach the blackbody, and electrons would be in Compton equilibrium with radiation at \(T \xi(T)^2=T_{\rm{BB}}\eta^2\), of which the Comptonization correction factor is \[\xi(T) \approx \max\left\{1,\frac{1}{2}\ln\left(y_{max}\right) \left[1.6+\ln\left(y_{max}\right)\right]\right\},\] where \(y_{max}=3~(\rho/10^{-9}\text{ g}\text{ cm}^{-3})^{-1/2} (T/100\text{ eV})^{\rm{9/4}}\). Moreover, pair production process limits the highest temperature, for which we set \(\sim 100~\rm{keV}\) [76]. Combining these analyses, the radiation temperature during the jet breakout can be determined by \[\label{Thbre} T_{\rm{h,bre}}=\min\left\{T_{\rm{h,Comp}}, 100~\rm{keV} \right\},\tag{9}\] where the Comptonization modified temperature is \[T_{\rm{h,Comp}}=T_{\rm{BB,hbre}} \begin{cases} \eta^2/\xi(T_{\rm{h,Comp}})^2 & \eta>1 \\ 1 & \eta<1. \end{cases}\]
The observed properties of the emission are shown in the first column of Figure 5. There exists a wide range of \(R\) that satisfies \(L_{\rm{h,bre}}>L_{\rm{bol,AGN}}\), with \(T_{\rm{h,bre}}\) generally exceeding \(O(10^6)\rm{K}\) at these regions, and consequently, the breakout emission can outshine the AGN disk background in X-ray bands. However, the observed emission typically exhibits a short duration with \(t_{\rm{h,bre}}<O(10^2)\text{ s}\), which is significantly shortened for a lighter AGN case, making the flare slightly hard to be detected. In addition, changing the system parameters, we find that the observable regions enlarge for the case with a smaller SMBH mass \(M\) or a lower kick velocity \(v_{\rm{k}}\), and the emission becomes more intense in the case of a smaller \(\alpha\) or a lower \(v_{\rm{k}}\), all of which facilitate the observation.
4.2 Emission from cooling disk cocoon↩︎
Given the resemblance, we investigate the emission produced by the expanding cocoon through an analogy with the cocoon’s radiation subsequent to the breakout of a gamma-ray burst jet from the star [76].
The energy deposited in the disk cocoon is \(E_{\rm{cd}} \approx E_{\rm{c}}/2\), primarily in the form of radiation. Same as the jet, the cocoon also undergoes a breakout from the AGN disk. For an opaque cocoon, following the breakout, the initial radiation energy is converted into the gas kinetic energy to drive its expansion. The terminal velocity of the disk cocoon material with mass, \(m_{\rm{c}}\simeq \rho_{\rm{AGN}} V_{\rm{c}}\), can be estimated as \(v_{\rm{c}}\simeq \sqrt{2 E_{\rm{cd}}/m_{\rm{c}}}\). Simplifying the expanding cocoon as a spherical shell with radius \(r_{\rm{c}}=V_{\rm{c}}^{1/3}+v_{\rm{c}}t_{\rm{exp}}\) at time \(t_{\rm{exp}}\) after the breakout, photons would diffuse out from the shell when its optical depth, \(\tau_{\rm{c}} \simeq \kappa m_{\rm{c}}/4 \pi r_{\rm{c}}^2\), roughly equals to \(c/v_{\rm{c}}\), the diffusion timescale is then given by \[\label{tdiffc} t_{\rm{diff,c}} \simeq \tau_{\rm{c}} \frac{r_{\rm{c}}}{c} =\left(\frac{\kappa m_{\rm{c}} }{4\pi v_{\rm{c}} c}\right)^{1/2},\tag{10}\] where \(\kappa=0.34\) for the ionized gas. Prior to photon effective diffusion, the cocoon undergoes adiabatic cooling, resulting in a reduction of internal radiation energy to \(E_{\rm{r,c}}\sim E_{\rm{cd}}V_{\rm{c}}^{\frac{1}{3}}/r_{\rm{c}}\), which is subsequently released over \(t_{\rm{diff,c}}\). Thereby, the luminosity of the disk cocoon cooling emission is \[\label{Lc} L_{\rm{c}}=\frac{E_{\rm{r,c}}}{t_{\rm{diff,c}}} \simeq\frac{2\pi c E_{\rm{c}}V_{\rm{c}}^{1/3}}{\kappa m_{\rm{c}}}.\tag{11}\]
The temperature of the disk cocoon at the breakout, \(T_{\rm{c,bre}}\), can be estimated similarly to Equation (9 ), where the thermal equilibrium temperature is modified to \[T_{\rm{BB,c}} = \left(\frac{E_{\rm{c}}}{2 a V_{\rm{c}}}\right)^{0.25},\] and the thermal coupling coefficient is changed to \[\eta_{\rm{c}} \equiv \frac{n_{\rm{BB}}\left(T_{\rm{BB,c}}\right)}{t_{\rm{bre}} \dot{n}_{\rm{ph},\rm{ff}}\left(T_{\rm{BB,c}}\right)} .\] After adiabatic cooling of radiation during the cocoon expansion, the temperature becomes \[\label{Tc} T_{\rm{c}}=T_{\rm{c,bre}}\frac{V_{\rm{c}}^{1/3}}{r_{\rm{c}}},\tag{12}\] which is, namely, the temperature of the disk cocoon cooling emission.
The above calculations are based on the assumption that \(\tau_{\rm{c}} \gg c/v_{\rm{c}}\) at the jet breakout, indicating that photons initially remain trapped within the disk cocoon. Conversely, when \(\tau_{\rm{c,bre}}\sim \kappa m_{\rm{c}}/4 \pi V_{\rm{c}}^{2/3} < c/v_{\rm{c}}\), photons would escape from the cocoon during the jet propagation within the AGN disk. In such a case, the failure of assuming an adiabatic cocoon leads to inaccuracies in the calculation of jet propagation and collimation in Section 3.2, and the intricate cooling process should be considered to investigate the concrete evolution of both jet and cocoon. For completeness, keeping the inaccuracy in mind, we estimate the observed properties of the disk cocoon cooling emission as follows: when \(\tau_{\rm{c,bre}} < c/v_{\rm{c}}\), the luminosity of emission is set as the jet power, \(L_{\rm{c}} \simeq 0.5 L_{\rm{jet}}\), i.e., photons escape after being spilled from the jet head; the duration of emission is set as \(t_{\rm{c}} \simeq t_{\rm{bre}} + t_{\rm{h,bre}}\), i.e., the duration of the jet releasing energy into the disk plus the time of radiation diffusing out from the disk. And the temperature is set as \(T_{\rm{c,bre}}\) at the jet breakout.
The observed properties of the emission are shown in the second column of Figure 5, where the dot dash lines indicate \(R\) regions with \(\tau_{\rm{c,bre}} < c/v_{\rm{c}}\), for which the radiation properties are inaccurate. First, from the perspective of total luminosity, \(L_{\rm{c}}\) is generally lower than \(L_{\rm{bol,AGN}}\), rendering the observation of the disk cocoon cooling emission challenging. Second, the radiation temperatures predominantly fall within UV bands except for the TQM model case, of which the temperature is higher because of the lower disk density resulting in an inefficient thermalization. Furthermore, the temperature primarily relies on the AGN disk properties rather than the specific BH accretion processes. Third, the emission duration, or the radiation diffusion timescale, primarily relies on the AGN disk properties, and typically spans less than one day. Additionally, our artificial setup for the emission properties in regions where \(\tau_{\rm{c,bre}} < c/v_{\rm{c}}\) has a negligible impact on the observation, because, in general, \(L_{\rm{c}}\) is significantly less than \(L_{\rm{bol,AGN}}\), thereby, the emission is unable to outshine the AGN background radiation and remain undetectable.
4.3 Emission from cooling jet cocoon↩︎
Similar to the disk cocoon, the internal energy of the jet cocoon is radiation dominated with a total deposited energy \(\sim E_{\rm{c}}/2\), which subsequently accelerates the rarer shocked materials after the jet breakout. Numerical simulations show that, during the jet propagation within dense medium, partial material mixing would take place between the two cocoon components [76], [84]–[86]. The mixed jet cocoon exhibits stratification, where the material near the base of jet is more mixed, thus colder and heavier; conversely, the material closer to the jet head experiences less mixing, thus hotter and lighter [87]. Additionally, the energy of the jet cocoon exhibits a roughly flat distribution per logarithmic scale of terminal proper velocity, corresponding to the energy per baryon of the shocked materials [85], [86]. So we estimate the fraction of the cocoon’s energy deposited in material with a specific \(\Gamma_{\rm{cj}} \beta_{\rm{cj}}\) as \(f_{\Gamma \beta} \sim 0.1\) following [76], with the Newtonian shocked jet material considered as a representative emission source due to its longer duration compared to the shorter-lived emission from the relativistic material. Though, in actuality, radiation is continuously emitted early from the relativistic material and later from the Newtonian material [76].
The mass of the jet cocoon material with a terminal velocity \(\Gamma_{\rm{cj}} \beta_{\rm{cj}} < 1\) \((\beta_{\rm{cj}} \lesssim 0.7)\) is estimated as \[m_{\rm{cj}} \simeq \frac{f_{\Gamma \beta} E_{\rm{c}}}{\beta_{\rm{cj}}^2 c^2},\] and the volume of the jet cocoon at the breakout is \[V_{\rm{cj}} \simeq \Sigma_{\rm{j}} (H-d_{\rm{bre}}).\] We define a critical velocity \(\beta_{\rm{cj,cr}}\) to represent the case of which photons begin to escape from the jet cocoon roughly at the jet breakout, i.e., \(\tau_{\rm{cj,bre}} \simeq \kappa m_{\rm{cj}}/V_{\rm{cj}}^{2/3} =1/\beta_{\rm{cj,cr}}\), and then \[\beta_{\rm{cj,cr}}= \frac{\kappa f_{\Gamma \beta} E_{\rm{c}}}{V_{\rm{cj}}^{2/3} c^2},\] where still we set \(\kappa = 0.34\) for an ionized medium. The photon is coupled with the jet cocoon material with \(\beta_{\rm{cj}}<\beta_{\rm{cj,cr}}\) at the jet breakout. Subsequently, the cocoon with mass \(m_{\rm{cj}}\) undergoes expansion and adiabatic cooling before eventually allowing for photon escape. This process remains largely unaffected by the faster material with \(\beta_{\rm{cj}}>\beta_{\rm{cj,cr}}\), due to the stratified jet cocoon exhibits preferential escape of the upper hotter material followed by the lower colder material [87].
Similar to Equation (11 ), the luminosity of the jet cocoon cooling emission is estimated as \[\label{Lcj} L_{\rm{cj}} =\frac{2\pi c f_{\Gamma \beta} E_{\rm{c}}V_{\rm{cj}}^{1/3}}{\kappa m_{\rm{cj}}} =\frac{2 \pi \beta_{\rm{cj}}^2 c^3 V_{\rm{cj}}^{1/3}}{\kappa},\tag{13}\] which is in proportion to \(\beta_{\rm{cj}}^2\). Considering only the Newtonian part of the shocked jet cocoon, we set \(\beta_{\rm{cj}}=0.7\) for cases with \(\beta_{\rm{cj,cr}}>0.7\), and set \(\beta_{\rm{cj}}=\beta_{\rm{cj,cr}}\) for cases with \(0.7>\beta_{\rm{cj,cr}}>v_{\rm{c}}/c\), to calculate the peak luminosity. And similar to Equation (10 ), the emission duration is estimated as the photon diffusion timescale, \[t_{\rm{diff,cj}} \simeq \left(\frac{\kappa m_{\rm{cj}} }{4\pi \beta_{\rm{cj}} c^2}\right)^{1/2} = \left(\frac{\kappa f_{\Gamma \beta} E_{\rm{c}} }{4\pi \beta_{\rm{cj}}^3 c^4}\right)^{1/2}.\] The radiation temperature \(T_{\rm{cj}}\) can be calculated similarly as Equation (9 ) and (12 ), by substituting the initial energy, mass, and volume to \(f_{\Gamma \beta} E_{\rm{c}}/2\), \(m_{\rm{cj}}\), and \(V_{\rm{cj}}\). Moreover, for emission with \(L_{\rm{cj,peak}}>L_{\rm{bol,AGN}}\), we also calculate \(t_{\rm{diff,cj}}\) and \(T_{\rm{cj}}\) at \(L_{\rm{cj}}=L_{\rm{bol,AGN}}\), adopting \(f_{\Gamma \beta} = 0.1\), to estimate the maximum duration for observation and the temperature evolution, since the energy and mass distribution of the jet cocoon, which can be described as \(dE/dv\propto v^{-n}\) and \(m(>v)\propto v^{-(n+1)}\) [76], [88], result in a luminosity evolution after the peak following \(L_{\rm{cj}} \propto t^{-4/(n+2)}\).
In the above we focus on the opaque part of the partial mixing jet cocoon, but when \(\beta_{\rm{cj,cr}}<v_{\rm{c}}/c\), the entire jet cocoon is transparent even though being fully mixed with the disk cocoon to possess a minimum velocity \(v_{\rm{c}}\). In these cases, in rough, we artificially set the luminosity, the emission duration, and the temperature as \(L_{\rm{cj}}=0.5L_{\rm{jet}}\), \(t_{\rm{cj}} \simeq t_{\rm{h,bre}} + t_{\rm{bre}}\), and \(T_{\rm{cj,bre}}\) for the material with velocity \(v_{\rm{c}}\).
The observed properties of the emission are shown in the third column of Figure 5. First, \(L_{\rm{cj}}\) surpasses \(L_{\rm{bol,AGN}}\) across a wide range of \(R\), thereby rendering the emission potentially detectable. The observation of systems with lower mass AGNs or slower kicked remnant BHs is more promising, owing to the dimmer AGN background radiation or the augmented jet power. Second, the temperatures of emission typically range \(O(10^6)-O(10^8)\rm{K}\), hence being observable in X-ray bands. Third, the duration of emission is generally less than one day, which is comparatively shorter than the disk cocoon cooling emission due to the higher velocity and lower mass of the jet cocoon material. Fourth, in the case of emission outshining the AGN background, since the energy distribution brings about radiation evolution, we find that at \(L_{\rm{cj}}=L_{\rm{bol,AGN}}\) (dotted lines in panels of \(T_{\rm{cj}}\) and \(t_{\rm{diff,cj}}\) in Figure 5), whereafter the source tends to become fainter than the AGN, the total duration of the observed emission ranges from a few \(O(10^2)\rm{s}\) to \(O(10^3)\rm{s}\), accompanied by a decrease in temperature making for softer radiation.
Note that, in this subsection, we explore the jet cocoon cooling emission in analogy with the gamma-ray burst jet breaking a collapsing star, of which the breakout time, \(t_{\rm{bre}}\lesssim 10\text{ s}\) [76], is much less than that of a jet breaking the AGN disk studied here. The prolongation of the propagation time would result in a more efficient mixing between the two cocoon components, thereby the maximum velocity of the jet cocoon material may be less than \(0.7c\) as set in gamma-ray burst jet system, causing a significant decline of the emission luminosity due to \(L_{\rm{cj}} \propto \beta_{\rm{cj}}^2\) demonstrated by Equation (13 ). To investigate the impact of a reduced \(\beta_{\rm{cj}}\), we consider a case of efficient mixing, where only \(10\%\) of the jet cocoon energy is deposited into a mixed Newtonian material with the maximum velocity \(\beta_{\rm{cj}}=5v_{\rm{c}}/c\), the relevant properties of the emission are shown in the third column of Figure 5. We find that the emission is still observable though the mixing leading to a weaker radiation with lower temperature.
4.4 Time delay between BBH merger and EM emission↩︎
Given that the EM radiation arises from the jet triggered by the kicked remnant BH, the time delay between a BBH merger event and its associated EM emission can be attributed to four factors: the potential remnant kick time \(t_{\rm{kick}}\), the jet formation time, which is approximately a few \(t_{\rm{BHL}}\) [65], the jet breakout time, denoted as \(t_{\rm{bre}}\), and the time before photons diffusing out effectively, taken as \(t_{\rm{diff,c}}\) and \(t_{\rm{diff,cj}}\), for the disk and jet cocoon cooling emission. Therefore, the time delay is estimated by \[t_{\rm{delay}} \simeq (t_{\rm{kick}}) + t_{\rm{BHL}} + t_{\rm{bre}} + t_{\rm{diff}},\] of which the values are shown in the last row of Figure 5, where we ignore \(t_{\rm{kick}}\) (values are shown in Figure 1). The dominant term of \(t_{\rm{delay}}\) for all of the three emission components shifts from \(t_{\rm{BHL}}\) to \(t_{\rm{bre}}\) as \(R\) increases, while the contribution from \(t_{\rm{diff}}\) of the disk and jet cocoon is found to be negligible. Moreover, in regions of \(L>L_{\rm{AGN,bol}}\), where the emission would outshine the AGN background, \(t_{\rm{delay}} \simeq t_{\rm{BHL}}\) is basically satisfied, indicating that the time delay between the emergence of the observed emission and the BBH merger is primarily determined by the jet formation timescale. For example, \(t_{\rm{delay}}\) is approximately \(154\), \(5\), and \(0.2~days\) for a \(100M_\odot\) remnant BH with kick velocity \(10^2\), \(10^{2.5}\), and \(10^3~\rm{km}\text{ s}^{-1}\), respectively. Alternatively, considering the cavity environment and incorporating \(t_{\rm{kick}}\), \(t_{\rm{delay}}\) is about \(8.8\), \(42.8\), and \(371.8~days\) for a \(100M_\odot\) remnant BH kicked with velocity \(10^{2.5}~\rm{km}\text{ s}^{-1}\) at \(100\), \(10^3\), and \(10^4R_{\rm{g}}\) of the AGN disk with a \(10^8M_\odot\) SMBH, respectively.
5 Discussion↩︎
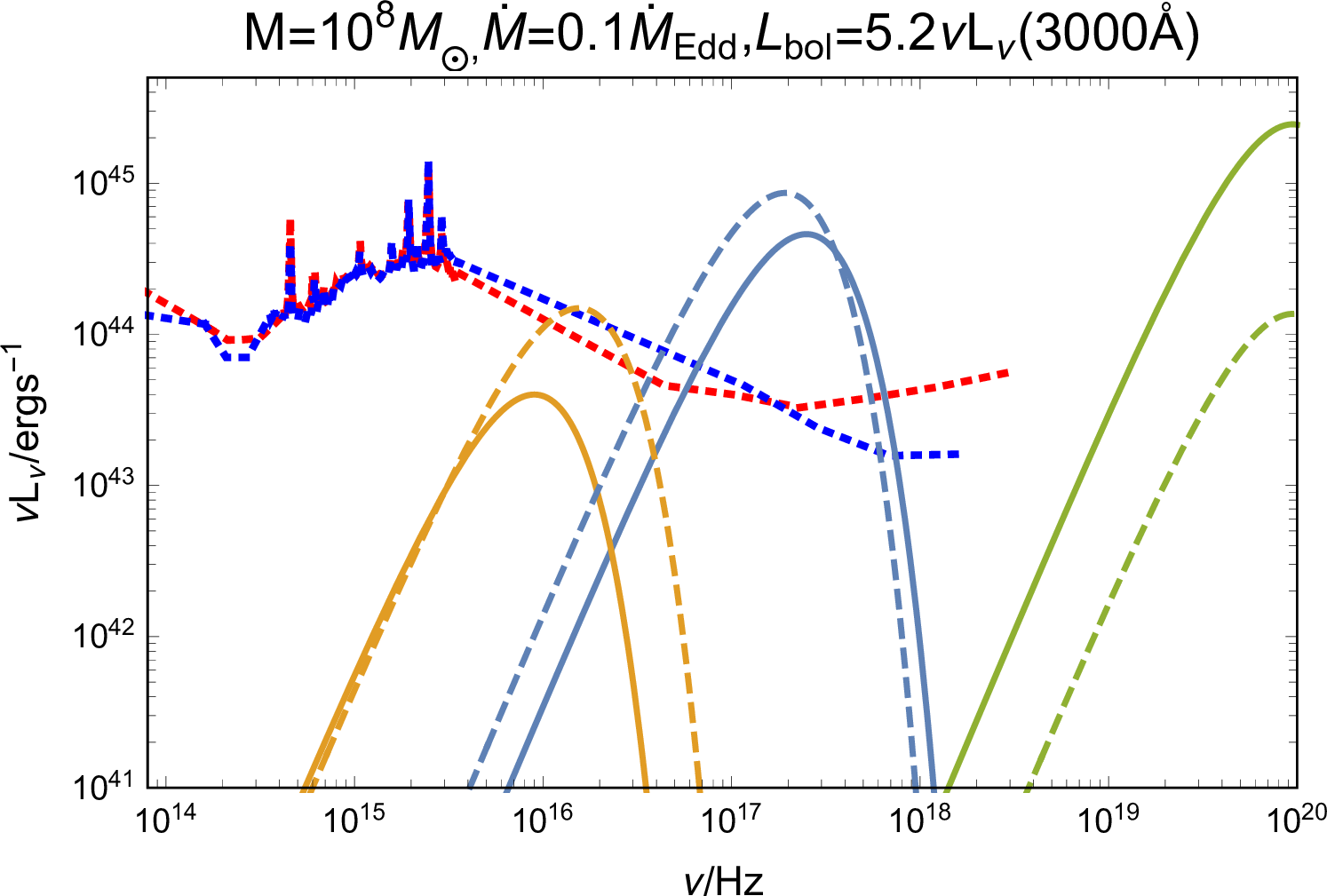
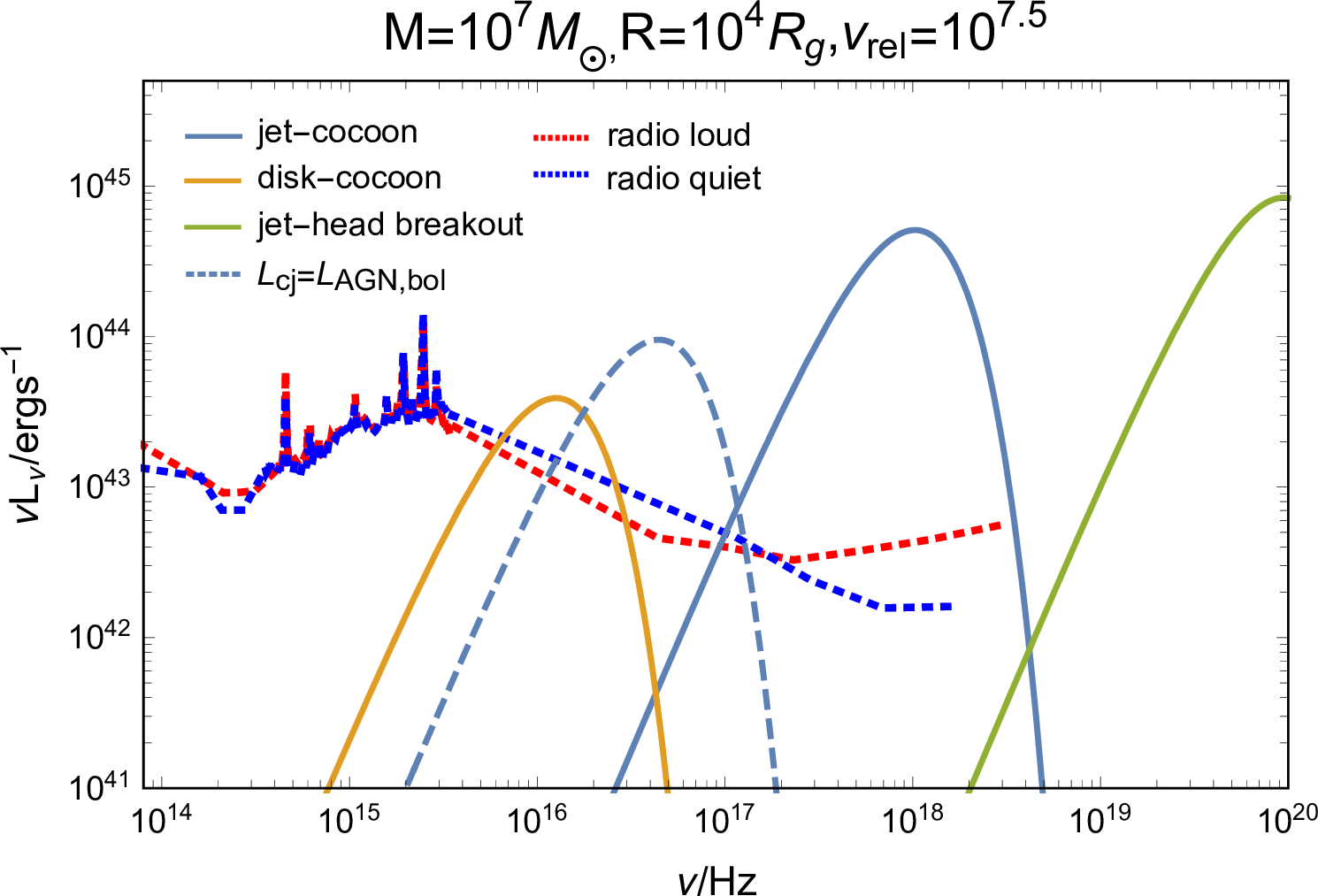
Figure 6: Spectra for emission from the breakout jet-head (green line), the cooling disk cocoon (golden line), and the cooling jet cocoon (navy-blue line). To express the AGN background, of which the spectra are shown by the red and blue dotted lines, we take the mean spectral energy distribution of radio loud and radio quiet quasars from [89], with the use of a scaling law \(\zeta(3000\mathring{A})=5.2\) in the correlation of \(L_{\rm{AGN,bol}}=\zeta\lambda L_{\lambda}\) [90]. The solid and dashed lines in \(M=10^8M_\odot\) panel represent a \(100M_\odot\) BBH merger occurring at \(700\) and \(10^4R_{\rm{g}}\), generating a kicked remnant with velocity \(10^{2.5}\) and \(10^{2}~\rm{km}\text{ s}^{-1}\), respectively. The solid line in \(M=10^7M_\odot\) panel represents a \(100M_\odot\) BBH merger occurring at \(10^4R_{\rm{g}}\) with the remnant kicked to \(10^{2.5}~\rm{km}\text{ s}^{-1}\), and the dashed line shows the spectra of jet cocoon cooling emission at \(L_{\rm{cj}}=L_{\rm{bol,AGN}}\)..
5.1 sec:Detectability↩︎
As demonstrated above, BBH mergers occurring within the AGN disk have the potential to generate observable EM counterparts, such as emission during the jet breakout, disk cocoon cooling emission, and jet cocoon cooling emission, which are powerful to outshine the AGN background radiation. Meanwhile, the emission exhibits significant variations with respect to \(R\) (see Figure 5), namely, the particular locations of BBH mergers, which are likely at migration traps around \(\sim 500-700 R_{\rm{g}}\) [28], [91], or alternatively at more distant radii of \(\sim 0.01~\rm{pc}\) for a \(4\times10^6M_\odot\) SMBH, corresponding to \(\sim 5\times 10^4 R_{\rm{g}}\) [16]. Hence, to predict the detectability of EM counterparts, we give illustrative examples, which depict the feasible BBH mergers in the AGN disk along with a successful emergence of powerful jet, the emblematic spectra for emission are shown in Figure 6.
As indicated by the three examples, i.e., a \(100M_\odot\) BBH merger occurring at \(700\), \(10^4\), and \(10^4R_{\rm{g}}\) in the AGN disk with a SMBH of \(10^8\), \(10^8\), and \(10^7M_\odot\), generating a kicked remnant with velocity \(10^{2.5}\), \(10^{2}\), and \(10^{2.5}~\rm{km}\text{ s}^{-1}\): First, the jet breakout emission exhibits a peak in hard X-ray bands \(\sim 100~\rm{keV}\), which could be detected by X-ray telescopes such as Swift BAT [92] and Fermi GBM [93] 2. The duration of the emission is \(0.21\), \(395\), and \(0.69\text{ s}\), respectively, suggesting a preference for the observation of mergers with a weakly kicked remnant at large radii in the disk of heavier SMBH. Second, the disk cocoon cooling emission peaks in EUV bands, the duration of which is \(3.0\times10^4\), \(3.0\times10^5\), \(2.2\times10^4\text{ s}\), much longer than the two other emission components. But the emission is unlikely to be observed because the EUV photons would be absorbed by gas and dust in the host galaxy, meanwhile, the optical/UV radiation is greatly covered by the more prominent AGN background. Third, the jet cocoon cooling emission peaks in soft X-ray band at \(\sim 1-10~\rm{keV}\), of which the duration is \(574\), \(7561\), \(374\text{ s}\). Moreover, the energy and mass distribution of jet cocoon material causes an extension of the observable duration, e.g., to \(1314\text{ s}\) for the third example (dashed line in the second panel of Figure 6), and an evolution of spectra to softer X-ray band, both of which are beneficial to observations via soft X-ray telescopes, e.g., Chandra [94], XMM-Newton [95], Swift XRT [96], Einstein Probe [97], and to the identification of EM counterparts. Additionally, the time delay for the three examples is approximately \(5\), \(154\), \(5~days\) (\(31\), \(1314\), \(80~days\) if the kicked remnant is initially in a cavity), respectively, disfavoring follow-up observations and identification of EM counterparts for merger systems which produce remnants with low kick velocity.
To conclude, a BBH merger event occurring within the AGN disk can produce a detectable soft X-ray counterpart deriving from the cooling jet cocoon, which persists for a period \(O(10^3)\text{ s}\) and appears after \(O(10)~days\) following the GW trigger. Observations prefer to systems leaving over BHs with larger kick velocity, which possess relatively short time delay; conversely, though a more weakly kicked remnant BH can generate more powerful emission, the large time delay makes it difficult to be identified as EM counterparts. In the future, with a more precise constraint on kick velocity through an accurate measurement of GW [98], we will be able to predict the EM counterparts more accurately, thereby providing better guidance for observations.
5.2 Jet direction, kick direction, and merger height↩︎
During the above calculations, we have adopted a typical system, of which the BBH merger occurs at the midplane of an AGN disk, generating a remnant BH kicked along the disk plane which drives a jet perpendicular to the disk plane. In this subsection, we discuss implications of varying the jet direction, the kick direction, and the merger height.
The jet driven by the BZ mechanism propagates along the BH spin direction, which may be random for mergers taking place in the AGN disk [9]. For a jet which is inclined at an angle \(\theta\) with respect to the AGN disk angular momentum direction, the propagation distance before its breakout is extended from \(\sim H\) to \(\sim H/\cos\theta\). Compared to the vertical case, at the jet breakout, we find approximately \(t_{\rm{bre}} \propto \cos\theta^{-5/3}\), \(\tilde{L} \propto \cos\theta^{4/3}\), and \(\beta_{\rm{h}} \propto \cos\theta^{2/3}\), indicating that the inclined jet spends more time to propagate within the AGN disk, and is more significantly collimated with a lower head’s velocity. Also, as \(E_{\rm{c}}\propto \cos\theta^{-5/3}\), more jet energy is deposited into the cocoon. Assuming that the jet breaking out from the head [37], we investigate the properties of associated emission. For jet breakout emission, the luminosity would decrease as \(L_{\rm{h,bre}}\propto \cos\theta^{2/3}\), and the duration is extended to \(t_{\rm{h,bre}}\propto \cos\theta^{-4/3}\). The typical radiation temperature undergoes a reduction and a more effective thermalization, with \(T_{\rm{BB,hbre}}\propto \cos\theta^{1/3}\) and \(\eta \propto \cos\theta^{5/2}\). The other two emission components exhibit similar properties. For disk cocoon cooling emission, we have \(L_{\rm{c}}\propto \cos\theta^{1/3}\), \(t_{\rm{diff,c}}\propto \cos\theta^{-11/6}\), and \(T_{\rm{BB,c}}\propto \cos\theta^{1/3}\), \(\eta \propto \cos\theta^{17/6}\). Besides, radiation temperature after cocoon adiabatic cooling varies as \(T_{\rm{c}}\propto T_{\rm{c,bre}} \cos\theta^{1/6}\). For jet cocoon cooling emission from the material with a specific \(\beta_{\rm{cj}}\), related properties are \(L_{\rm{cj}}\propto \cos\theta^{-7/9}\), \(t_{\rm{diff,cj}}\propto \cos\theta^{-5/6}\), and \(T_{\rm{BB,cj}}\propto \cos\theta^{1/6}\), \(\eta \propto \cos\theta^{9/4}\), \(T_{\rm{cj}}\propto T_{\rm{cj,bre}} \cos\theta^{1/18}\), respectively. In fact, [39] investigated a limiting case of a jet propagating quasi-parallel to the AGN disk plane with \(\theta=82^\circ\); an optical flare lasting for \(O(100)~days\) is produced by the disk cocoon, of which the temperature is lower and the duration is longer than the perpendicular case we studied, as expected.
The kick direction of the remnant BH could be random because of an isotropic distribution of the orbital plane direction of merging BBHs ([9], but when binary-single interaction is 2D and confined roughly to the AGN disk midplane, the kick direction is almost along the disk, see e.g. [26]). For a kick inclined to the AGN disk plane, the remnant BH would have moved to a high altitude when a jet forms after a few \(t_{\rm{BHL}}\). Likewise, for the merger of a BH binary whose orbit around SMBH is misaligned with the AGN disk, the starting point of the BH-driven jet would be located away from the midplane. At the side of the AGN disk where the kicked BH is closer to the disk surface, an off-midplane jet would break out of the AGN disk more easily with a shorter propagation distance, and may generate brighter and shorter-duration radiation with higher temperature; on the contrary, the same jet needs to propagate a longer distance to break out of the other side of the AGN disk, generating dimmer and lower-temperature emission with longer duration.
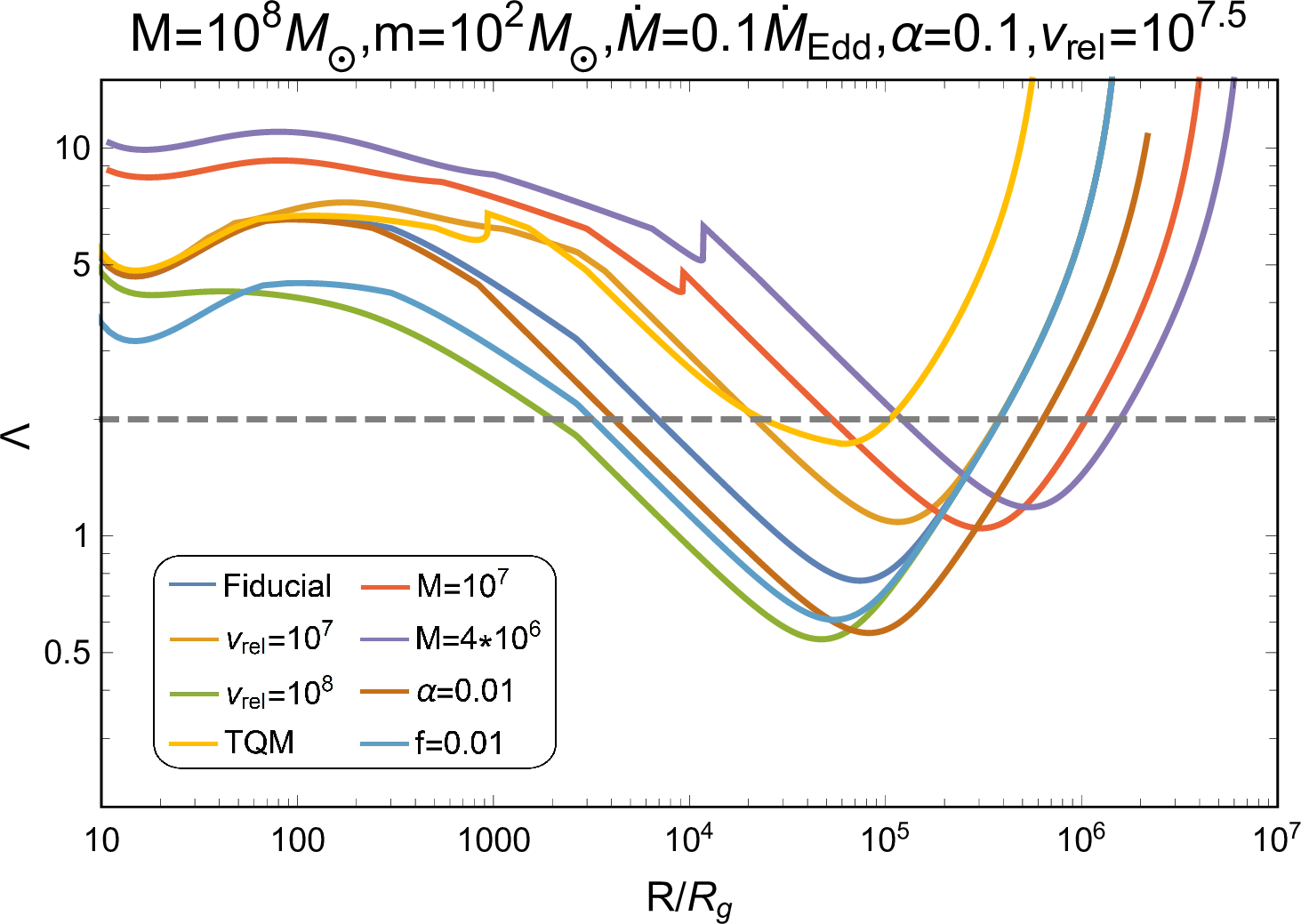
Figure 7: Criterion \(\Lambda\) from Equation (14 ) as a function of \(R\) for different system parameters. The dashed line represents \(\Lambda=2\), above which the jet propagation is stable, unaffected by the magnetically driven external kink instability.
5.3 Stability of jet during propagation↩︎
As mentioned above, the jet driven by a kicked remnant BH is magnetized. Even though the jet behaves as a hot, hydrodynamic one during its propagation, the magnetic effects would still bring about an external kink instability, which generates helical motions of the entire jet, increasing its effective cross-section and reducing its propagation velocity, even causing it to stall [75]. We employ a criterion proposed by [75], which describes a comparison between the instability development timescale and the dynamic timescale, to examine the instability, \[\label{kink} \Lambda \simeq 20\sqrt{\frac{2\pi}{9}} \left(\frac{L_{\rm{jet}}}{\rho_{\rm{AGN}} (H-d_{\rm{bre}})^2\gamma_{\rm{j}}^2c^3}\right)^{1/6},\tag{14}\] where \(\gamma_{\rm{j}}=\theta_0^{-1}\) is set. For \(\Lambda>2\), as suggested by [75], the external kink is weak and the jet propagates similarly to a hydrodynamic one; on the contrary, the jet is markedly deformed, which would be stalled and fail to break out the AGN disk.
Values of \(\Lambda\) as a function of \(R\) are shown in Figure 7. \(\Lambda\) decreases as \(R\) increases because of the thickening of the AGN disk, and jets are more unstable for larger SMBH mass or less jet power cases. At relatively large radii, where \(\Lambda<2\), jets would experience significant deceleration or disruption caused by the external kink instability. Consequently, our calculations of the jet propagation and the associated EM emission may be inaccurate in these regions. However, jets with \(L_{\rm{jet}}>L_{\rm{AGN,bol}}\), which can produce observable emission, generally possess \(\Lambda>2\), and hence are stable to the external kink. Therefore, our prediction for the EM counterparts should be acceptable.
6 Summary↩︎
In this work, we have explored the EM counterparts to BBH mergers occurring within the AGN disk. The merger remnant BH, which undergoes a natal kick due to asymmetric GW radiation, would traverse the magnetized AGN disk environment and launch a jet via the BZ mechanism. Interaction between the jet and the AGN disk during its propagation leads to jet collimation and energy dissipation, thereby driving various EM emissions. We have investigated three specific processes as sources of radiation, namely, the jet breakout, the disk cocoon cooling, and the jet cocoon cooling. Among these processes, only the emission from the cooling jet cocoon exhibits a higher potential for detection. Accordingly, a soft X-ray transient that outshines the AGN background can be identified as an EM counterpart, exhibiting a duration of \(O(10^3)\text{ s}\) and emerging after a time delay of \(O(10)~days\) following the GW trigger.
We have found that the EM emission properties, including luminosity, temperature, duration, and time delay, are significantly influenced by the GW kick. Therefore, in the future, with improved GW measurements, a more precise constraint on kick velocity can facilitate the prediction of EM counterparts to BBH mergers in the AGN disk and guide subsequent follow-up observations. If such multimessenger signals are indeed detected, it would confirm the formation of binary mergers in the AGN disk, and provide valuable insights into the evolution of compact objects and binaries embedded in AGN disks.
It should be noted that a key assumption has been made in this work, namely the successful launch of a powerful jet by the kicked remnant BH, which necessitates a strongly magnetized environment. However, the magnetization properties of the AGN disk, or even the disk itself, have not been well studied. For instance, the uncertain degree of ionization in the disk outer region may lead to decoupling between gas and magnetic field, thereby suppressing magnetorotational instability and magnetic field amplification, which hinders the jet formation. So we suggest that a more comprehensive understanding of AGN disks is imperative for investigating the EM counterparts associated with the embedded BBH merger events.
We would like to thank the referee for valuable comments and helpful suggestions. This work was supported by the National SKA Program of China (grant No. 2020SKA0120300), and the National Natural Science Foundation of China (grant No. 11833003).
7 Opacity and Optical Depth of AGN Disk in Propagation Path of jet↩︎
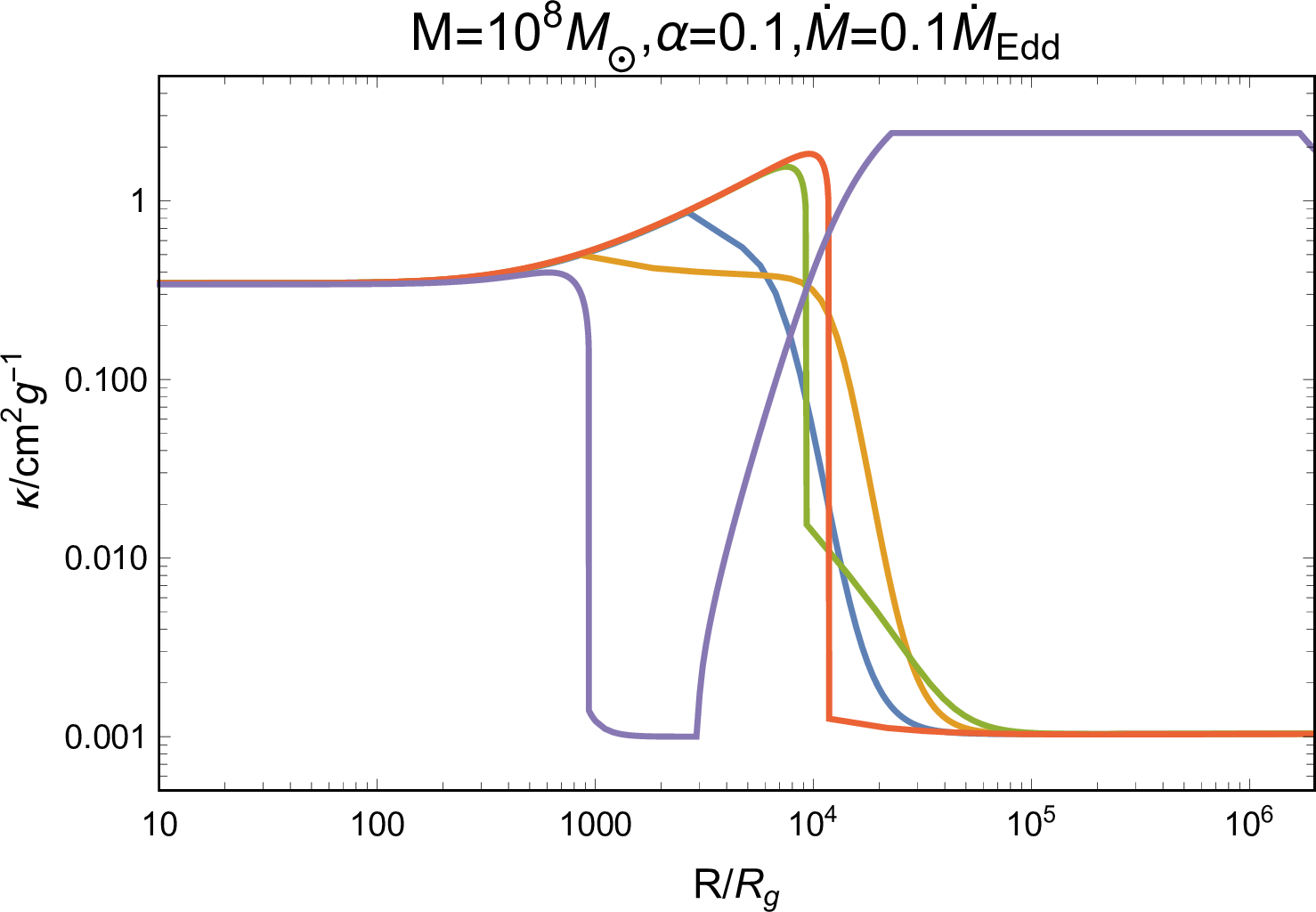
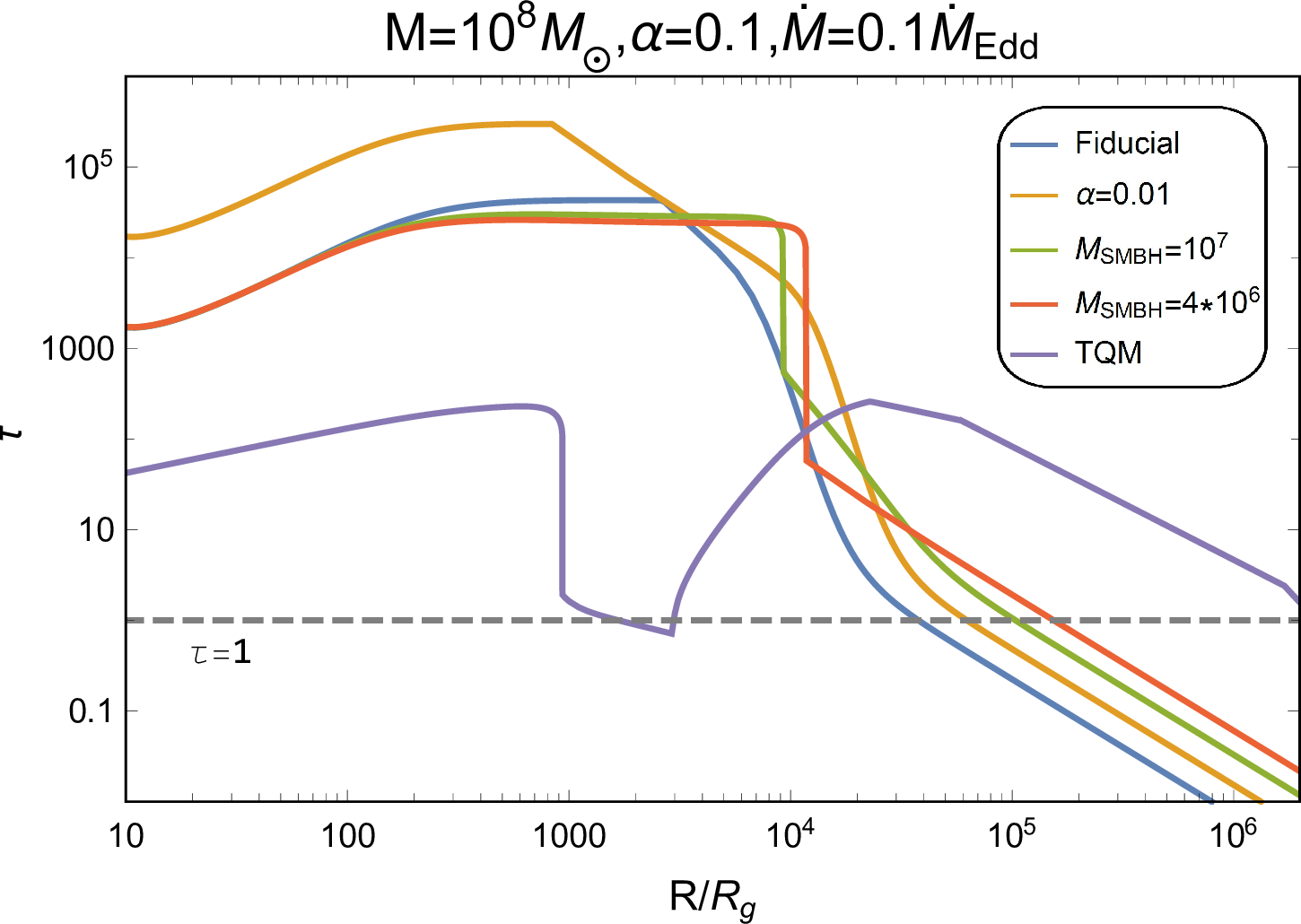
Figure 8: Dependence of opacity and optical depth on \(R\) for various AGN disk models and parameters (the inset shows these parameters), of which the fiducial values are \(M=10^{8}\rm{M}_{\odot}\), \(\alpha=0.1\), \(\dot{M}=0.1 \dot{M}_{\rm{Edd}}\) adopting SG model. The dashed line in the right panel represents the threshold \(\tau=1\)..
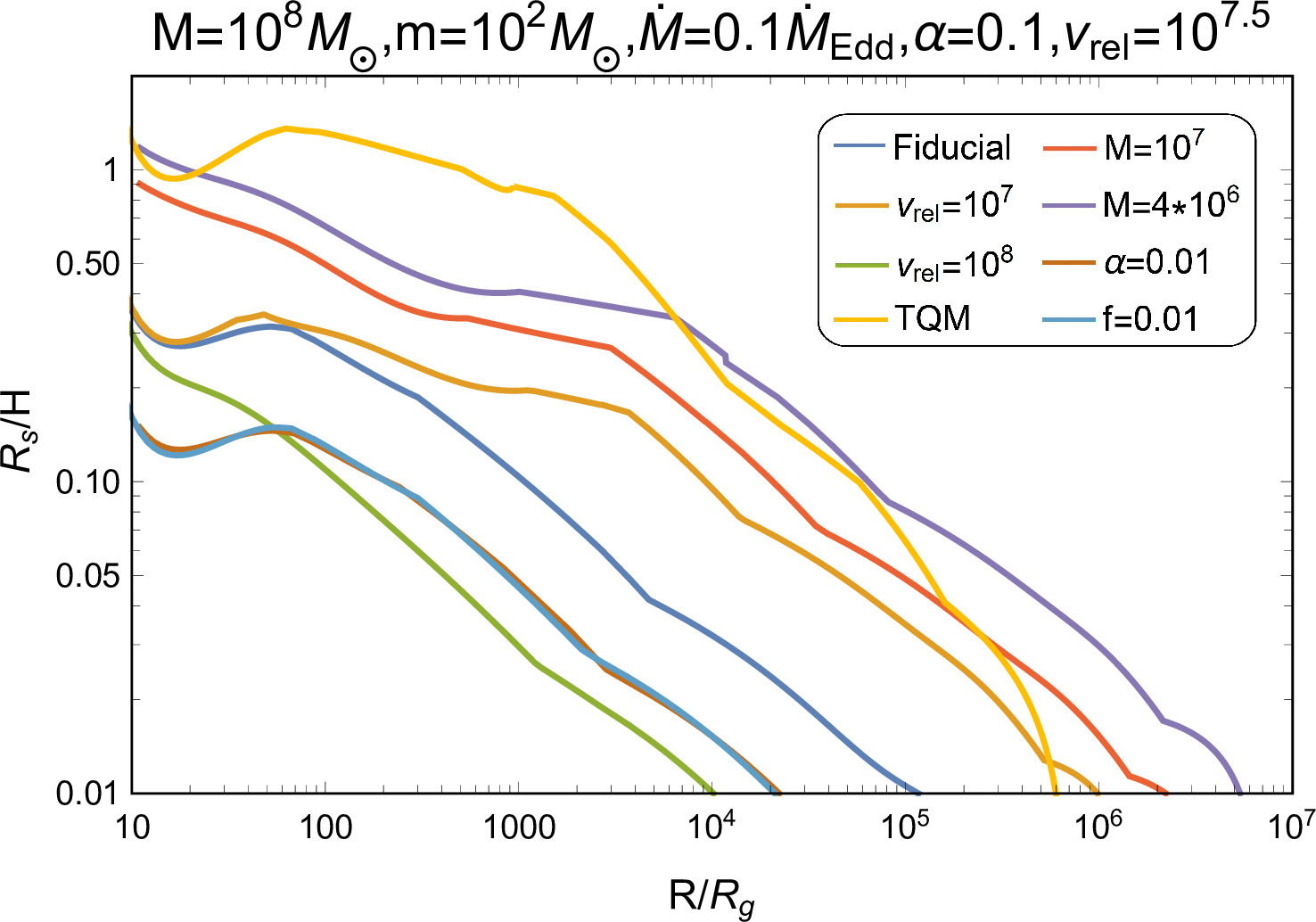
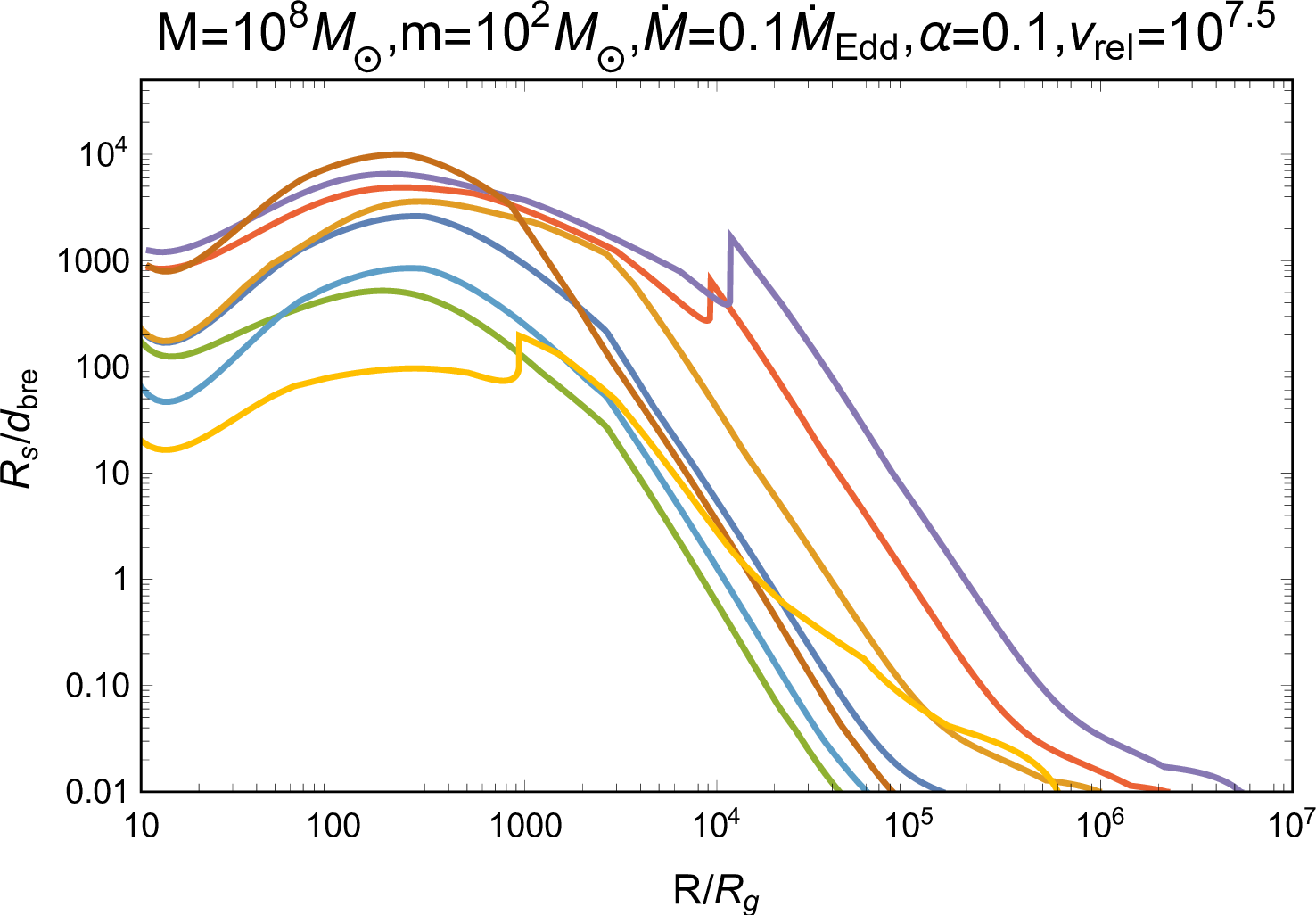
Figure 9: Comparison of the Strömgren radius with the AGN disk height and the thickness of the jet-head breakout shell for various system parameters. The left and right panel shows \(R_{\rm{S}}/H\) and \(R_{\rm{S}}/d_{\rm{bre}}\), respectively..
When calculating the structures of AGN disks, we have employed the approximate expression for the opacity proposed in [99]; the opacity and optical depth properties of AGN disks are shown in Figure 8. \(\kappa_{\rm{AGN}}\) and \(\tau_{\rm{AGN}}\) drop sharply at \(O(10^3)R_{\rm{g}}\) and \(>O(10^4)R_{\rm{g}}\) for TQM and SG models, by reason of the gas recombination at disk temperature ranging \(10^3-10^4\text{ K}\) [44]. Thus, the AGN disk is optically thin to its own radiation at these regions, but it would still be opaque to photons with energy \(>13.6 ~\rm{eV}\) (the ionization energy of Hydrogen atom) because of the absorption by neutral gas [46]. As shown in Figure 5, photons generated by the BH-driven jet-cocoon systems always have characteristic temperatures \(>10^5\text{ K}\), which would thereby ionize the neutral gas and cannot directly escape the initially “optically thin”AGN disk.
To specifically analyze the propagation of jet photons, we estimate the maximum ionization distance for the jet-head shock photons with temperature of Equation (9 ), via the Strömgren radius [100], \[R_{\rm{S}}=\left(\frac{3}{4 \pi} \frac{S}{n_{\rm{AGN}}^{2} \beta_{2}}\right)^{1 / 3},\] where \(S=L_{\rm{h,bre}}/(k T_{\rm{h,bre}})\) is the photon emission rate, \(n_{\rm{AGN}}=\rho_{\rm{AGN}}/m_{\rm{p}}\), and \(\beta_{2}=2 \times 10^{-10}T_{\rm{h,bre}}^{-3 / 4}\rm{~cm}^{3}\rm{~s}^{-1}\). As shown in Figure 9, we find that \(R_{\rm{S}}<H\), which means that the environment exhibits high opacity and photons cannot escape from the jet-cocoon system, maintaining the radiation-dominated jet head and cocoon; we also find that \(R_{\rm{S}}>d_{\rm{bre}}\), thereby the ambient gas above the jet head has been ionized at its breakout and our assumption of \(\kappa_{\rm{AGN}}=0.34\text{ cm}^2\text{ g}^{-1}\) holds except for the very outer AGN disk regions, where the BH-driven jet is too weak to ionize the medium.
References↩︎
Note that after the submission of this paper, [38] was posted online, which also investigates the cocoon cooling emission resulting from a jet produced by the BBH merger remnant embedded in an AGN disk. The differences lie in the treatment of mass rate accreted onto the merger remnant and the time delay between GW trigger and EM emission. In [38], a jet launch occurs immediately after the merger; in our study, a jet would be launched following a sufficient accumulation of magnetic field around the kicked remnant BH during its traversal through AGN environment. By combining emissions with various time delays, a more distinctive EM counterpart can be identified.↩︎
Properties of various telescopes, e.g., detection bandpass, sensitivity, and field of view, are summarized in Table 3 of [37].↩︎