Improving Hyperparameter Learning under Approximate Inference in Gaussian Process Models
January 01, 1970
Abstract
Approximate inference in Gaussian process (GP) models with non-conjugate likelihoods gets entangled with the learning of the model hyperparameters. We improve hyperparameter learning in GP models and focus on the interplay between variational inference (VI) and the learning target. While VI’s lower bound to the marginal likelihood is a suitable objective for inferring the approximate posterior, we show that a direct approximation of the marginal likelihood as in Expectation Propagation (EP) is a better learning objective for hyperparameter optimization. We design a hybrid training procedure to bring the best of both worlds: it leverages conjugate-computation VI for inference and uses an EP-like marginal likelihood approximation for hyperparameter learning. We compare VI, EP, Laplace approximation, and our proposed training procedure and empirically demonstrate the effectiveness of our proposal across a wide range of data sets.
1 Introduction↩︎
Gaussian processes [1] provide a plug-and-play approach for inference and learning, with principled ways of incorporating prior knowledge over functions and quantifying uncertainty. While GP regression under a conjugate (Gaussian) likelihood can be carried out elegantly in closed form, we focus on the non-conjugate case, where exact inference is intractable. Training of the GP consists of inferring the approximate posterior and learning the hyperparameters of the model. For clarity, by training we refer to the combination of inference and learning.
In a supervised learning setting, GPs are typically trained to optimize performance on the training samples [2]. Under the GP paradigm, the go-to solution to learning is finding \(\boldsymbol{\theta}^\star\) that maximizes the marginal likelihood. The marginal likelihood summarizes the probability that we would generate the observations \(\mathbf{y}\) with the model parameters \(\boldsymbol{\theta}\) if we would sample over the prior. It is formed by marginalizing over the latent functions from the GP prior, thus also known as the evidence. Even if this does not capture all aspects of generalization [3], [4], it is still used as a practical proxy for performance on unseen test points (see 1 for the proxy and test performance on the ionosphere benchmark data set).

Figure 1: Practical benefits on Ionosphere: Marginal likelihood (top) acts as a training proxy for predictive density (bottom) of unseen future data. Our training objective produces a better point for prediction that also matches the MCMC baseline.
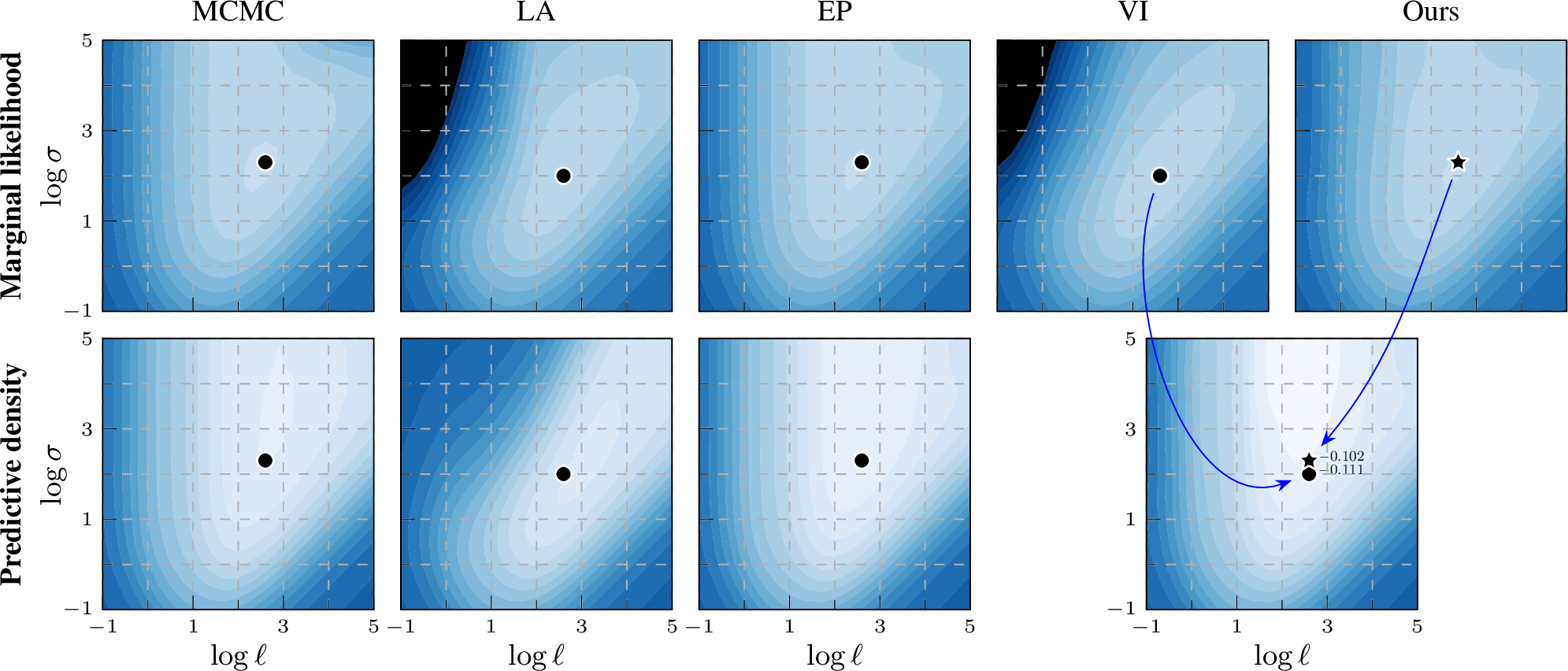
Figure 2: Log marginal likelihood / predictive density surfaces for the ionosphere data set by varying kernel magnitude \(\sigma\) and lengthscale \(\ell\).
The colour scale is the same in all plots: \(-0.8\)  \(0\) (normalized by \(n\)). Optimal
hyperparameters are shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages the same variational representation as
VI.
\(0\) (normalized by \(n\)). Optimal
hyperparameters are shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages the same variational representation as
VI.
Under approximate inference, the marginalization step entangles the representation of the posterior with the learning target evaluation. The common approach is to assume an approximative Gaussian form for the posterior, so that the inference problem turns into finding a ‘good’ parameterization for the Gaussian [5]. The simplest approach is the so-called Laplace’s approximation [6], which uses a second-order Taylor approximation. It is efficient but not very accurate. Variational inference [7] and expectation propagation [8] are two commonly used approximate inference methods for non-conjugate GP models, which have complementary advantages: VI optimizes a lower bound of the marginal likelihood, is easy to implement, straightforward to use, and the convex optimization problem is guaranteed to converge. However, it is known to underestimate variance [9]. EP on the other hand requires implementation-wise tuning per likelihood and is not guaranteed to converge [10]. However, it does provide a good approximation for the marginal likelihood [11], [12].
For model performance on unseen test data, the learning of hyperparameters plays a crucial role. Thus we strongly advocate against the common practice of jointly optimizing variational and hyperparameters using the ELBO, as the training target is only representative for the variational parameters. We build on work by [13] and [14] that separate the learning of hyperparameters from inferring the variational parameters, and capture a link between VI and EP: the approximate posterior obtained through VI has exactly the same structure as the approximate posterior of EP. We obtain an EP-like marginal likelihood estimate from the VI approximate posterior for full and sparse GPs with no added computational cost. We propose a hybrid training procedure that combines the complementary advantages of natural-gradient VI and EP.
The contributions of this paper are as follows. (i) We improve generalizability in non-conjugate GP models with no extra computational cost by augmenting VI with an EP-like learning target for hyperparameter learning. (ii) We demonstrate our EP-like learning target is closer to an MCMC baseline and thus provides a better learning objective. We empirically compare the quality of the approximate marginal likelihood in LA, EP, and VI, and our proposed learning target. (iii) We show our method improves generalizability via experiments in binary classification for full and sparse GP models and robust regression.
2 Approximate Inference↩︎
In this section, we review common approximate inference methods in Gaussian process (GP) models. GP models put a GP prior over functions: \[\text{GP prior:} \quad f(\mathbf{x}) \sim \mathcal{GP}(\mu(\mathbf{x}), \kappa(\mathbf{x},\mathbf{x}')),\] where \(\mathbf{x}\in \mathcal{X} \subset \mathbb{R}^d\) is an input vector, \(\mu(\mathbf{x})\) is the mean function, and \(\kappa(\mathbf{x},\mathbf{x}')\) is the covariance (kernel) function. This GP prior is linked to the data set \(\mathcal{D}=(\mathbf{X}, \mathbf{y})=\{(\mathbf{x}_i, y_i)\}_{i=1}^n\) of input–output pairs through a likelihood function that maps the latent function value \(f(\mathbf{x})\) to the observations. We assume the likelihood factorizes over observations: \[\textstyle \text{Likelihood:}\quad \mathbf{y}\,|\,\mathbf{f}\sim \prod_{i=1}^{n} p(y_i \,|\,f(\mathbf{x}_i)).\] The posterior is given by \(p(\mathbf{f}\,|\,\mathbf{y}; \boldsymbol{\theta})\propto p(\mathbf{y}\,|\,\mathbf{f};\boldsymbol{\theta})\, p(\mathbf{f};\boldsymbol{\theta})\), where \(\boldsymbol{\theta}\) denotes the model (hyper)parameters of the likelihood, mean function, and kernel, and \(\mathbf{f}\) is the vector of function values evaluated at the inputs. Prediction at a new test input \(\mathbf{x}_*\) is obtained by computing the predictive distribution \(p(f(\mathbf{x}_*)\,|\,\mathcal{D}, \mathbf{x}_*)\).
Probabilistic inference For (conjugate) Gaussian likelihoods, \(p(y_i \,|\,f_i) = \mathrm{N}(y_i \,|\,f(\mathbf{x}_i), \sigma_\text{n}^2)\), the posterior is available in closed form as a Gaussian distribution. For non-Gaussian likelihood models the inference problem needs to be approached with approximative inference methods. Sampling schemes (see [sec:mcmc] for our baseline solution) can tackle this, but for efficient inference one typically employs an approximative Gaussian posterior of the form \[\label{eq:posterior} \text{Approximate posterior:} \quad q(\mathbf{f}) = \mathrm{N}(\mathbf{m},\mathbf{S}).\tag{1}\] Its ‘optimal’ parameterization [7] is given in terms of \(2n\) parameters \((\boldsymbol{\alpha},\boldsymbol{\beta})\) such that \(\mathbf{m}= \mathbf{K}\boldsymbol{\alpha}\) and \(\mathbf{S}= (\mathbf{K}^{-1} + \operatorname{diag}(\boldsymbol{\beta}))^{-1}\), where \(\mathbf{K}\) is an \(n \times n\) matrix with \(\kappa(\mathbf{x}_i,\mathbf{x}_j)\) as the \(ij\)th entry. The inference problem thus turns into (efficiently) finding a (good) representation of the posterior in terms of 1 by minimizing some measure of error. Typical approaches for this are the Laplace approximation (local linearisation of the problem), expectation propagation (approximately minimizing \(\operatorname{D_{\mathrm{KL}}}\big[p(\mathbf{f}\,|\,\mathbf{y}) \,\big\|\, q(\mathbf{f}) \big]\) from approximate to true posterior), or variational inference (minimizing \(\operatorname{D_{\mathrm{KL}}}\big[q(\mathbf{f}) \,\big\|\, p(\mathbf{f}\,|\,\mathbf{y}) \big]\)). EP is expected to be the most accurate method [3] and Laplace to have the smallest computational overhead.
Learning under the GP paradigm In probabilistic machine learning, ‘learning’ typically amounts to finding point estimates for the hyperparameters \(\boldsymbol{\theta}\) in the likelihood, mean function, and kernel by optimizing w.r.t.the log marginal likelihood: \[\text{Learning target:}\quad \boldsymbol{\theta}^\star = \arg \max_{\boldsymbol{\theta}} \log p(\mathbf{y}; \boldsymbol{\theta}).\] For Gaussian likelihoods, the marginal likelihood is available in closed form. For non-conjugate models, we can only optimize a proxy to the marginal likelihood \(p(\mathbf{y}; \boldsymbol{\theta}) = \int p(\mathbf{y}\,|\,\mathbf{f};\boldsymbol{\theta})\, p(\mathbf{f};\boldsymbol{\theta})\,\mathrm{d}\mathbf{f}\), which depends on the approximate inference scheme and how it represents the posterior.
2.1 Laplace Approximation (LA)↩︎
A local Taylor expansion of the log posterior gives the Laplace approximation [6]. By defining \(\Psi(\mathbf{f})=\log (p(\mathbf{y}\,|\,\mathbf{f})\,p(\mathbf{f};\boldsymbol{\theta}))\), the approximate posterior \(q(\mathbf{f})\) is obtained through a second-order Taylor expansion of \(\Psi(\mathbf{f})\) around its maximum at \(\hat{\mathbf{f}}=\arg \max_{\mathbf{f}} \Psi(\mathbf{f})\) (the posterior mode): \(p(\mathbf{f}\,|\,\mathbf{y}; \boldsymbol{\theta})\propto \exp(\Psi(\mathbf{f})) \approx \exp\big(\Psi(\hat{\mathbf{f}})+\frac{1}{2} (\mathbf{f}-\hat{\mathbf{f}})^\top \nabla^2 \Psi(\mathbf{f}) |_{\mathbf{f}=\hat{\mathbf{f}}} (\mathbf{f}-\hat{\mathbf{f}})\big)\). This is proportional to \(\mathrm{N}(\mathbf{f}\,|\,\hat{\mathbf{f}}, \mathbf{A}^{-1}) = q(\mathbf{f})\), where \(\mathbf{A}= -\nabla^2 \Psi(\mathbf{f})|_{\mathbf{f}=\hat{\mathbf{f}}}\) is the Hessian of the negative log posterior at \(\hat{\mathbf{f}}\). The log marginal likelihood is approximated as \[\begin{gather} \textstyle\log p(\mathbf{y}; \boldsymbol{\theta}) = \log \int \exp (\Psi(\mathbf{f})) \,\mathrm{d}\mathbf{f}\\ \approx \textstyle\log \int \exp\big(\Psi(\hat{\mathbf{f}})-\frac{1}{2} (\mathbf{f}-\hat{\mathbf{f}})^\top \mathbf{A}(\mathbf{f}-\hat{\mathbf{f}})\big) \,\mathrm{d}\mathbf{f}. \end{gather}\]
2.2 Expectation Propagation (EP)↩︎
Expectation Propagation [8] is based on an approximation \(q(\mathbf{f})\) that factorizes in the same way as the target posterior \(p(\mathbf{f}\,|\,\mathbf{y}; \boldsymbol{\theta})\propto p(\mathbf{f};\boldsymbol{\theta})\prod_{i=1}^n p(y_i \,|\,f_i ;\boldsymbol{\theta})\): each likelihood term is approximated with a site function \(t_{i}(f_{i}; \boldsymbol{\zeta}_{i})\), and \[\label{eq:full95ep95post} \textstyle q(\mathbf{f}; \boldsymbol{\theta}, \boldsymbol{\zeta}) \propto p(\mathbf{f};\boldsymbol{\theta})\prod_{i=1}^n t_{i}(f_{i}; \boldsymbol{\zeta}_{i}).\tag{2}\] For GP models, the sites \(t_{i}(f_{i}; \boldsymbol{\zeta}_{i})\) are chosen to be (unnormalized) Gaussians, and hence the global approximation \(q(\mathbf{f})\) is also Gaussian. EP aims to minimize \(\operatorname{D_{\mathrm{KL}}}\big[p(\mathbf{f}\,|\,\mathbf{y}; \boldsymbol{\theta}) \,\big\|\, q(\mathbf{f}; \boldsymbol{\theta}, \boldsymbol{\zeta}) \big]\) w.r.t.\(\boldsymbol{\zeta}\). This KL cannot be computed directly. Instead, EP updates the sites in an iterative fashion; the parameters of one site \(\boldsymbol{\zeta}_i\) are tuned by minimizing the local Kullback–Leibler divergence \[\begin{gather} \label{eq:full95ep95infer95obj} \textstyle\operatorname{D_{\mathrm{KL}}}\big[p(y_i \,|\,f_i ;\boldsymbol{\theta})\, p(\mathbf{f};\boldsymbol{\theta})\, \prod_{j \neq i} t_{j}(f_{j}; \boldsymbol{\zeta}_{j})\\ \,\big\|\, t_{i}(f_{i}; \boldsymbol{\zeta}_{i})\,p(\mathbf{f};\boldsymbol{\theta})\textstyle\prod_{j \neq i} t_{j}(f_{j}; \boldsymbol{\zeta}_{j}) \big] , \end{gather}\tag{3}\] where in the first argument the \(n-1\) other likelihood terms have been replaced by their current site approximation. The optimal values of \(\boldsymbol{\zeta}_i\) in this step can be determined by matching the first two moments. This iterative process often works well in practice, but can be numerically unstable (e.g., for Student-\(t\) likelihood) and is not guaranteed to converge in the general case [10].
The log marginal likelihood is directly approximated as \[\label{eq:full95ep95energy} \log p(\mathbf{y}; \boldsymbol{\theta}) \approx \mathcal{L}_{\text{EP}}(\boldsymbol{\zeta}, \boldsymbol{\theta}) = \log \int p(\mathbf{f};\boldsymbol{\theta}) \prod_{i=1}^n t_{i}(f_{i}; \boldsymbol{\zeta}_{i}) \,\mathrm{d}\mathbf{f},\tag{4}\] which is known to lead to a good objective for learning hyperparameters [15].
2.3 Variational Inference (VI)↩︎
Variational Inference [7] approximates the GP posterior \(p(\mathbf{f}\,|\,\mathbf{y}; \boldsymbol{\theta})\) with a Gaussian distribution \(q(\mathbf{f}; \boldsymbol{\xi})\) parameterized by \(\boldsymbol{\xi}\). VI minimizes the reverse KL \(\operatorname{D_{\mathrm{KL}}}\big[q(\mathbf{f}; \boldsymbol{\xi}) \,\big\|\, p(\mathbf{f}\,|\,\mathbf{y}; \boldsymbol{\theta}) \big]\) by maximizing the following evidence lower bound (ELBO): \[\begin{gather} \label{eq:full95elbo} \!\!\!\!\! \log p(\mathbf{y}; \boldsymbol{\theta}) \geq \mathcal{L}_{\text{VI}}(\boldsymbol{\xi}, \boldsymbol{\theta}) = \sum_{i=1}^n \mathbb{E}_{q(f_i; \boldsymbol{\xi}_i)}\big[\log p(y_i \,|\,f_i; \boldsymbol{\theta})\big]\\ -\operatorname{D_{\mathrm{KL}}}\big[q(\mathbf{f}; \boldsymbol{\xi}) \,\big\|\, p(\mathbf{f}; \boldsymbol{\theta}) \big], \end{gather}\tag{5}\] w.r.t.variational parameters \(\boldsymbol{\xi}\). VI optimizes a lower bound on the marginal likelihood, so is guaranteed to converge, which is a strength over EP. As known from [16] and motivated by [17], it has been desirable to not use the optimal parameterization in terms of \(2n\) parameters, as the resulting optimization problem is non-convex. Instead, it is common to declare a variational distribution over the full posterior, \(q(\mathbf{f}; \boldsymbol{\xi})=\mathrm{N}(\mathbf{m}, \mathbf{S})\), and optimize the ELBO w.r.t.this mean–covariance parameterization1 \(\boldsymbol{\xi}= (\mathbf{m}, \mathbf{S})\) using a general-purpose optimizer [19].
In practice, the same lower bound \(\mathcal{L}_{\text{VI}}(\boldsymbol{\xi}, \boldsymbol{\theta})\) is used to optimize variational parameters as well as hyperparameters, i.e., inference and learning are coupled into a single optimization. This approach is commonplace, even though it is well-known to result in biased hyperparameters [9], [11], [12].
3 Learning in the Dual Parameterization↩︎
We design a hybrid training procedure that augments VI with an EP-like learning target for hyperparameter learning. Our work builds upon the dual parameterization [13]. Because the Gaussian distribution is part of the exponential family, we can write the approximate posterior as \(q(\mathbf{f}) = \mathrm{N}(\mathbf{m}, \mathbf{S}) = \exp \big(\boldsymbol{\eta}^{\top} \mathbf{T}(\mathbf{f})-a(\boldsymbol{\eta})\big)\), where \(\boldsymbol{\eta}=(\mathbf{S}^{-1} \mathbf{m},-\frac{1}{2} \mathbf{S}^{-1})\), \(\mathbf{T}(\mathbf{f})=(\mathbf{f}, \mathbf{f}\mathbf{f}^{\top})\) are the sufficient statistics, and \(\exp(-a(\boldsymbol{\eta}))\) is a normalization term. This leads to two additional parameterizations of \(q(\mathbf{f})\): using the natural parameters \(\boldsymbol{\eta}\), or using the expectation parameters \(\boldsymbol{\mu}=\mathbb{E}_{q(\mathbf{f})}[\mathbf{T}(\mathbf{f})]=(\mathbf{m}, \mathbf{S}+\mathbf{m}\mathbf{m}^{\top})\).
[13] showed that in the natural parameterization of the approximate posterior, natural gradient descent [20] (in the natural parameters space \(\boldsymbol{\eta}\)) will have the same computational cost as ordinary gradient descent on \(\boldsymbol{\xi}= (\mathbf{m}, \mathbf{S})\). The approximate posterior under this parameterization is \[\label{eq:full95vi95post} q(\mathbf{f}; \boldsymbol{\lambda}, \boldsymbol{\theta}) \propto p(\mathbf{f}; \boldsymbol{\theta}) \textstyle \prod_{i=1}^n \underbrace{\exp{\langle \boldsymbol{\lambda}_i, \mathbf{T}(f_i)\rangle}}_{\triangleq~t_{i}(f_{i}; \boldsymbol{\lambda}_{i})},\tag{6}\] where \(\boldsymbol{\lambda}_i=\nabla_{\boldsymbol{\mu}_i} \mathbb{E}_{q(f_i; \boldsymbol{\lambda}_i,\boldsymbol{\theta})}[\log p(y_i \,|\,f_i ;\boldsymbol{\theta})]\). The natural parameters of the approximate posterior \(q(\mathbf{f})\) are \(\boldsymbol{\eta}=\boldsymbol{\lambda}_0 + \boldsymbol{\lambda}\), where \(\boldsymbol{\lambda}_0=(\boldsymbol{0}, -\frac{1}{2} \mathbf{K}^{-1})\) are the natural parameters of the prior \(p(\mathbf{f};\boldsymbol{\theta})\) and \(\boldsymbol{\lambda}\) are the parameters of the likelihood approximation term \(t(\mathbf{f})\). Then, we could also parameterize the approximate posterior with \(\boldsymbol{\lambda}\), to which we refer as the ‘dual’ \(\boldsymbol{\lambda}\) parameterization.
Crucially, the approximate posterior 6 has the same form as its EP counterpart 2 . This links EP with VI, which is the starting point for our proposed learning objective. The similarity per se has been visible in, e.g., [14], [21], but it had not been explored further.

Figure 3: Training procedure for improved hyperparameter learning by a VEM-style iteration.
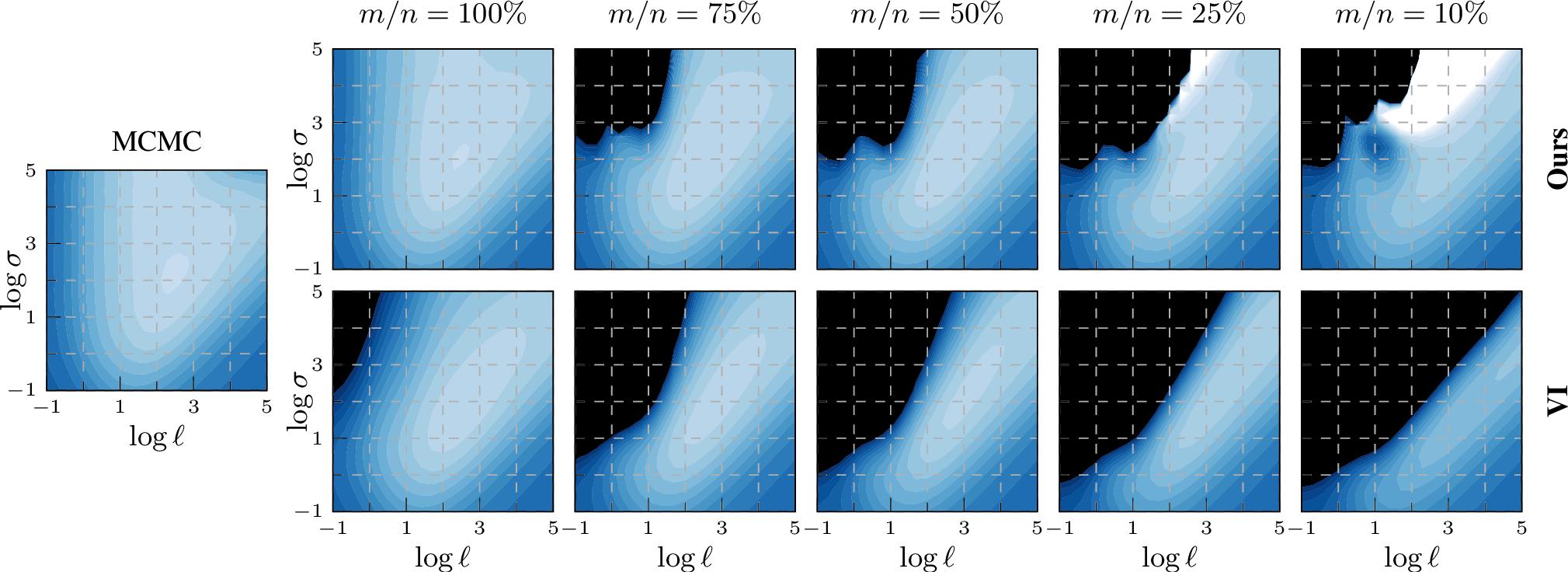
Figure 4: Sparse approximation: log marginal likelihood surfaces for the ionosphere data set, changing the fraction \(m/n\) of the number of inducing points \(m\) vs.\(n=351\) data points. The colour scale is the same in all plots: \(-0.8\)  \(0\); values below the predefined range are plotted as black. For moderate sparsification, our EP-like marginal likelihood estimation (top) matches the full MCMC baseline better than VI (bottom). For extreme sparsification
(\(10\%\): \(m=35\)), neither approximation resembles the full surface.
\(0\); values below the predefined range are plotted as black. For moderate sparsification, our EP-like marginal likelihood estimation (top) matches the full MCMC baseline better than VI (bottom). For extreme sparsification
(\(10\%\): \(m=35\)), neither approximation resembles the full surface.
3.1 Our Proposed Objective for Learning↩︎
Natural gradient descent can efficiently optimize the variational parameters \(\boldsymbol{\lambda}\), and we can combine it with another optimizer for the hyperparameters, leading to a natural separation of the inference and learning steps [22]. As discussed by [14], this can be seen as a Variational Expectation–Maximization (VEM) procedure. Under this setup, inference/learning is performed by alternating between optimizing the variational distribution in the \(\boldsymbol{\lambda}\) parameterization and taking gradient steps for finding \(\boldsymbol{\theta}\) by iterating the following steps at the \(k\)th iteration: \[\begin{align} &\text{E-step (inference):} \quad \boldsymbol{\lambda}^{(k+1)} \leftarrow \arg \max _{\boldsymbol{\lambda}} \mathcal{L}_\mathrm{E}(\boldsymbol{\lambda}, \boldsymbol{\theta}^{(k)}), \\ &\text{M-step (learning):} \quad \boldsymbol{\theta}^{(k+1)} \leftarrow \arg \max _{\boldsymbol{\theta}} \mathcal{L}_\mathrm{M}(\boldsymbol{\lambda}^{(k+1)}, \boldsymbol{\theta}), \end{align}\] where the objective for both the inference and learning steps is the ELBO in 5 under the \(\boldsymbol{\lambda}\) parameterization: \(\mathcal{L}_\mathrm{E} \equiv \mathcal{L}_\mathrm{M} \equiv \mathcal{L}_{\text{VI}}\). Note: Even if the parameterization and optimization procedure are different, the inference and learning objective are the same as in 2.3 and typically expected to converge at the same optima.
VEM deals with the variational inference problem by casting inference into an optimization problem that is solved by NGD, which appears both principled and efficient. We conjecture that the ELBO in 5 is not the best objective. Conveniently, the dual parameterization in the VI posterior 6 is formed as a product of the prior and Gaussian sites \(t_{i}(f_{i}; \boldsymbol{\lambda}_{i})\) just as in EP (cf.@eq:eq:full95ep95post ). This provides a representation of the posterior that is directly EP-like and allows us to estimate the log marginal likelihood by plugging \(\boldsymbol{\lambda}_i\) from 6 into \(\boldsymbol{\zeta}_i\) in 4 : \[\label{eq:epobj} \mathcal{L}_\mathrm{M} \equiv \mathcal{L}_\text{EP} (\boldsymbol{\lambda}, \boldsymbol{\theta})= \log \!\!\int\!\! p(\mathbf{f};\boldsymbol{\theta})\textstyle\prod_{i=1}^n t_{i}(f_{i}; \boldsymbol{\lambda}_{i}) \,\mathrm{d}\mathbf{f},\tag{7}\] giving the target for the M-step.
Our hybrid training procedure uses the variational objective in the E-step to ensure a good representation of the posterior. Then in the M-step, we use an EP-like (and thus closer to marginal likelihood) objective for hyperparameter learning, at no additional computational cost. The algorithm is sketched out in 3. Although our procedure requires implementing two training objectives, this is not likelihood-specific and has minimal implementation overhead.
4 Sparse Approximation for Large Data Sets↩︎
Regardless of conjugacy, inference in GP models for large-scale data sets is challenging due to an \(\mathcal{O}(n^3)\) computational bottleneck. In this section, we extend our hybrid training procedure to the sparse case.
A common approach to tackle this scalability issue is to summarize the information contained in the original data set into a smaller but more effective pseudo-data set, making the computational complexity tractable [23]. The pseudo-inputs are referred to as inducing points and denoted as \(\mathbf{Z}=\{\mathbf{z}_{i}\}_{i=1}^{m}\), where \(m \ll n\) [23]–[26]. The pseudo-outputs are referred to as inducing variables and denoted as \(\mathbf{u}=f(\mathbf{Z})\).
One common choice for the form of approximate posterior, as first introduced in [27], is \(q(\mathbf{f}, \mathbf{u}; \boldsymbol{\xi}_{\mathbf{u}}, \boldsymbol{\theta}) = p(\mathbf{f}\,|\,\mathbf{u}; \boldsymbol{\theta})\, q(\mathbf{u};\boldsymbol{\xi}_{\mathbf{u}})\), where \(p(\mathbf{f}\,|\,\mathbf{u})\) is the GP conditional and \(q(\mathbf{u};\boldsymbol{\xi}_{\mathbf{u}})=\mathrm{N}(\mathbf{m}_{\mathbf{u}}, \mathbf{S}_{\mathbf{u}})\) the approximate posterior in \(\mathbf{u}\). In this form, \(\mathbf{y}\) can only affect \(\mathbf{f}\) through \(\mathbf{u}\), which means the information in the original data set is summarized in \(\mathbf{u}\). The marginal posterior over the function \(f(\cdot)\) is \[\label{eq:svgp95marginals} q_{\mathbf{u}}(f(\cdot); \boldsymbol{\xi}_{\mathbf{u}}, \boldsymbol{\theta})= \int p(f(\cdot) \,|\,\mathbf{u}; \boldsymbol{\theta}) \, q(\mathbf{u}; \boldsymbol{\xi}_{\mathbf{u}}) \, \,\mathrm{d}\mathbf{u},\tag{8}\] where \(p(f(\cdot) \,|\,\mathbf{u};\boldsymbol{\theta})\) is the distribution of the GP prior conditioned on \(f(\mathbf{Z}) = \mathbf{u}\). Variational parameters \(\boldsymbol{\xi}_{\mathbf{u}}=(\mathbf{m}_{\mathbf{u}}, \mathbf{S}_{\mathbf{u}})\) can be inferred by optimizing the following ELBO: \[\begin{gather} \label{eq:sparse95elbo} \log p(\mathbf{y}; \boldsymbol{\theta}) \geq \mathcal{L}_{\text{VI}}^\text{sparse}(\boldsymbol{\xi}_{\mathbf{u}}, \boldsymbol{\theta}) \\ =\textstyle \sum_{i=1}^n \mathbb{E}_{q_{\mathbf{u}}(f_i; \boldsymbol{\xi}_{\mathbf{u}}, \boldsymbol{\theta})}[\log p(y_i \,|\,f_i; \boldsymbol{\theta})] \\ -\operatorname{D_{\mathrm{KL}}}\big[q(\mathbf{u};\boldsymbol{\xi}_{\mathbf{u}}) \,\big\|\, p(\mathbf{u};\boldsymbol{\theta}) \big], \end{gather}\tag{9}\] where \(q_{\mathbf{u}}(f_i; \boldsymbol{\xi}_{\mathbf{u}}, \boldsymbol{\theta})=\mathrm{N}(f_i \,|\,\mathbf{a}_i^{\top} \mathbf{m}_{\mathbf{u}}, \kappa_{i i}-\mathbf{a}_i^{\top}(\mathbf{K}_{\mathbf{u u}}-\mathbf{S}_{\mathbf{u}}) \mathbf{a}_i)\), \(\mathbf{a}_i=\mathbf{K}_{\mathbf{u}\mathbf{u}}^{-1} \mathbf{k}_{\mathbf{u},i}\), \(\mathbf{K}_{\mathbf{u}\mathbf{u}}= \kappa(\mathbf{Z}, \mathbf{Z})\), and \(\mathbf{k}_{\mathbf{u},i}=\kappa(\mathbf{Z}, \mathbf{x}_i)\) for the \(i\)th data sample. Now under the dual parameterization, we denote the converged dual parameters of the posterior marginal \(q_{\mathbf{u}}^*(f_i)\) as \(\boldsymbol{\lambda}_i^*\). [14] suggest designing a similar VEM procedure that exploits the structure of the \(q(\mathbf{u})\) in terms of the \(2n\) dual parameters. The natural parameters of \(q^*(\mathbf{u})\) are \[\begin{align} &(\mathbf{S}_{\mathbf{u}}^*)^{-1}\mathbf{m}_{\mathbf{u}}^* = \mathbf{K}_{\mathbf{u}\mathbf{u}}^{-1} \underbrace{ \big( \textstyle\sum_{i=1}^{n} \mathbf{k}_{\mathbf{u}i} {\lambda}_{1,i}^*\big) }_{= \bar{\boldsymbol{\lambda}}_1^*} \\ &(\mathbf{S}_{\mathbf{u}}^*)^{-1} = \mathbf{K}_{\mathbf{u}\mathbf{u}}^{-1} + \mathbf{K}_{\mathbf{u}\mathbf{u}}^{-1} , \underbrace{\big(\textstyle\sum_{i=1}^{n} \mathbf{k}_{\mathbf{u}i} {\lambda}_{2,i}^* \mathbf{k}_{\mathbf{u}, i}^\top \big)}_{\bar{\boldsymbol{\Lambda}}^*_2} \mathbf{K}_{\mathbf{u}\mathbf{u}}^{-1} , \end{align}\] where the quantities \(\mathbf{K}_{\mathbf{u}\mathbf{u}}\) and \(\mathbf{k}_{\mathbf{u},i}\) directly depend on \(\boldsymbol{\theta}\) and we can express the ELBO as the partition function of a Gaussian distribution. [14] use a tied parameterization [9], [28] that relaxes the need of storing all the \(\{\boldsymbol{\lambda}_i^*\}_{i=1}^n\) and instead stores only \(\bar{\boldsymbol{\lambda}}^*_1\) (length \(m\)) and \(\bar{\boldsymbol{\Lambda}}^*_2\) (size \(m\times m\)), which avoids the storage issue for large data sets. This extends the results of [13] to the sparse case where the resulting approximate posterior is \[\begin{gather} \label{eq:sparse95vi95post} q(\mathbf{f}, \mathbf{u}; \boldsymbol{\lambda}_{\mathbf{u}}, \boldsymbol{\theta}) \propto p(\mathbf{f}\,|\,\mathbf{u}; \boldsymbol{\theta})\,p(\mathbf{u};\boldsymbol{\theta}) \\ \times \textstyle \prod_{i=1}^n \underbrace{\exp{\langle\boldsymbol{\lambda}_{\mathbf{u},i}, \mathbf{T}(\mathbf{a}_i^{\top} \mathbf{u})\rangle}}_{\triangleq~t_i(\mathbf{u}; \boldsymbol{\lambda}_{\mathbf{u},i})}, \end{gather}\tag{10}\] where \(\boldsymbol{\lambda}_{\mathbf{u},i}=\nabla_{\boldsymbol{\mu}_{\mathbf{u}, i}} \mathbb{E}_{q_{\mathbf{u}}(f_i; \boldsymbol{\lambda}_{\mathbf{u},i}, \boldsymbol{\theta})}[\log p(y_i \,|\,f_i ;\boldsymbol{\theta})]\). This gives rise to the sparse E-step for inference under the sparse VEM scheme, where \(\mathcal{L}_\mathrm{E}^\text{sparse} \equiv \mathcal{L}_{\text{VI}}^\text{sparse}\).
Our proposed sparse objective for learning In EP, the tied representation for constraining the problem to a summary \(\boldsymbol{\zeta}_{\mathbf{u}}\) that scales in \(m\) rather than \(n\) gives rise to a sparse expectation propagation approach [9], where the log marginal likelihood is approximated as \[\begin{align} \label{eq:sparse95ep95energy} &\log p(\mathbf{y};\boldsymbol{\theta}) \approx \mathcal{L}_{\text{EP}}^\text{sparse}(\boldsymbol{\zeta}_{\mathbf{u}}, \boldsymbol{\theta}) \nonumber = \log \int q(\mathbf{f}, \mathbf{u}; \boldsymbol{\zeta}_{\mathbf{u}}, \boldsymbol{\theta}) \,\mathrm{d}\mathbf{f}\,\mathrm{d}\mathbf{u}\\ &~= \log \int p(\mathbf{f}\,|\,\mathbf{u};\boldsymbol{\theta}) \, p(\mathbf{u}; \boldsymbol{\theta}) \prod_{i=1}^n {t_i(\mathbf{u};\boldsymbol{\zeta}_{\mathbf{u},i})} \,\mathrm{d}\mathbf{f}\,\mathrm{d}\mathbf{u}. \end{align}\tag{11}\] Under dual parameterization VI, the approximate posterior 10 has the same structure as the EP approximate posterior in 11 . An EP-like estimate of the log marginal likelihood can thus be calculated by injecting \(\boldsymbol{\lambda}_{\mathbf{u},i}\) from 10 into \(\boldsymbol{\zeta}_{\mathbf{u},i}\) in 11 , thus giving \(\mathcal{L}_\mathrm{M}^\text{sparse} \equiv \mathcal{L}_{\text{EP}}^\text{sparse}(\boldsymbol{\lambda}_{\mathbf{u}}, \boldsymbol{\theta})\) which is a sparse EP-like learning objective under sparse variational inference. Note: \(\mathcal{L}_{\text{EP}}^\text{sparse}(\boldsymbol{\lambda}_{\mathbf{u}}, \boldsymbol{\theta})\) has the same computational cost as VI.
5 Experiments↩︎
We provide a range of experiments, in which we demonstrate effectiveness and practicality of the proposed approach, and highlight similarities and differences between learning under the three most common approximative inference methods (LA, EP, and VI).
As the log marginal likelihood is a surrogate for the generalization ability of the model to unseen data, we evaluate the marginal likelihood estimations of different methods (5.1) to see whether our EP-like marginal likelihood provides a better learning target. We then evaluate our hybrid training on non-conjugate tasks in binary classification and Student-\(t\) regression on small and mid-sized data sets ([sec:benchmarks] [sec:robust]).
How the sparsity affects the learning target is not obvious, therefore in 5.4 we first investigate the influence of sparse approximation on the learning target. We then evaluate our hybrid training procedure on binary classification tasks with sparse approximation. For all experiments in the main paper, we use an isotropic Matérn-\(\frac{5}{2}\) kernel. We also provide results under automatic relevance determination (ARD) with the same kernel (in 10.4), where we only include results for data sets that could be confirmed to have converged.
We implement the variational methods in GPflow [29], use reference implementations of LA and EP from GPy [30], and base our MCMC implementation on the GPML toolbox [31]. Additionally, we use the GPstuff toolbox [32] for the custom LA and EP implementation for the Student-\(t\) likelihood. We implement EP and VI convergence checks; details in 10.4.
7pt
| (\(n\), \(d\)) | LA | EP | VI | Ours | MCMC | |
|---|---|---|---|---|---|---|
| trains | (10, 30) | \(-0.702{\pm}0.025\) | \(\boldsymbol{-}0.698{\pm}0.033\) | \(-0.702{\pm}0.037\) | \(\boldsymbol{-}0.691{\pm}0.046\) | \(-0.692{\pm}0.025\) |
| balloons | (16, 5) | \(-0.660{\pm}0.125\) | \(-0.650{\pm}0.128\) | \(-0.649{\pm}0.185\) | \(\boldsymbol{-}0.607{\pm}0.227\) | \(-0.684{\pm}0.076\) |
| fertility | (100, 10) | \(\boldsymbol{-}0.388{\pm}0.122\) | \(\boldsymbol{-}0.384{\pm}0.149\) | \(\boldsymbol{-}0.393{\pm}0.136\) | \(\boldsymbol{-}0.397{\pm}0.139\) | \(-0.382{\pm}0.126\) |
| pittsburg-bridges-T-OR-D | (102, 8) | \(\boldsymbol{-}0.299{\pm}0.081\) | \(-0.321{\pm}0.108\) | \(\boldsymbol{-}0.290{\pm}0.110\) | \(\boldsymbol{-}0.293{\pm}0.116\) | \(-0.306{\pm}0.115\) |
| acute-nephritis | (120, 7) | \(-0.203{\pm}0.012\) | \(-0.046{\pm}0.007\) | \(-0.007{\pm}0.002\) | \(\boldsymbol{-}0.005{\pm}0.002\) | \(-0.005{\pm}0.002\) |
| acute-inflammation | (120, 7) | \(-0.184{\pm}0.018\) | \(-0.052{\pm}0.007\) | \(-0.007{\pm}0.002\) | \(\boldsymbol{-}0.007{\pm}0.002\) | \(-0.007{\pm}0.003\) |
| echocardiogram | (131, 11) | \(-0.424{\pm}0.093\) | \(\boldsymbol{-}0.418{\pm}0.095\) | \(\boldsymbol{-}0.425{\pm}0.110\) | \(-0.428{\pm}0.112\) | \(-0.437{\pm}0.127\) |
| hepatitis | (155, 20) | \(\boldsymbol{-}0.370{\pm}0.071\) | \(-0.372{\pm}0.072\) | \(\boldsymbol{-}0.364{\pm}0.090\) | \(-0.367{\pm}0.094\) | \(-0.369{\pm}0.091\) |
| parkinsons | (195, 23) | \(-0.260{\pm}0.031\) | \(-0.295{\pm}0.056\) | \(-0.160{\pm}0.050\) | \(\boldsymbol{-}0.141{\pm}0.046\) | \(-0.145{\pm}0.044\) |
| breast-cancer-wisc-prog | (198, 34) | \(\boldsymbol{-}0.458{\pm}0.075\) | \(-0.473{\pm}0.091\) | \(\boldsymbol{-}0.457{\pm}0.085\) | \(\boldsymbol{-}0.460{\pm}0.088\) | \(-0.464{\pm}0.085\) |
| spect | (265, 23) | \(\boldsymbol{-}0.593{\pm}0.049\) | \(\boldsymbol{-}0.590{\pm}0.055\) | \(-0.594{\pm}0.054\) | \(-0.595{\pm}0.054\) | \(-0.596{\pm}0.051\) |
| statlog-heart | (270, 14) | \(-0.395{\pm}0.064\) | \(\boldsymbol{-}0.389{\pm}0.061\) | \(-0.396{\pm}0.071\) | \(-0.397{\pm}0.071\) | \(-0.397{\pm}0.070\) |
| haberman-survival | (306, 4) | \(\boldsymbol{-}0.530{\pm}0.053\) | \(-0.532{\pm}0.059\) | \(-0.531{\pm}0.055\) | \(-0.531{\pm}0.055\) | \(-0.520{\pm}0.063\) |
| ionosphere | (351, 34) | \(-0.224{\pm}0.042\) | \(-0.230{\pm}0.042\) | \(\boldsymbol{-}0.170{\pm}0.048\) | \(\boldsymbol{-}0.170{\pm}0.055\) | \(-0.179{\pm}0.058\) |
| horse-colic | (368, 26) | \(-0.463{\pm}0.059\) | \(\boldsymbol{-}0.452{\pm}0.057\) | \(-0.467{\pm}0.072\) | \(-0.473{\pm}0.082\) | \(-0.469{\pm}0.079\) |
| congressional-voting | (435, 17) | \(-0.640{\pm}0.028\) | \(\boldsymbol{-}0.639{\pm}0.030\) | \(-0.641{\pm}0.030\) | \(-0.642{\pm}0.029\) | \(-0.644{\pm}0.027\) |
| cylinder-bands | (512, 36) | \(-0.488{\pm}0.038\) | \(-0.500{\pm}0.041\) | \(-0.465{\pm}0.049\) | \(\boldsymbol{-}0.451{\pm}0.052\) | \(-0.451{\pm}0.049\) |
| breast-cancer-wisc-diag | (569, 31) | \(-0.085{\pm}0.026\) | \(-0.140{\pm}0.020\) | \(-0.077{\pm}0.044\) | \(\boldsymbol{-}0.075{\pm}0.045\) | \(-0.076{\pm}0.043\) |
| ilpd-indian-liver | (583, 10) | \(\boldsymbol{-}0.513{\pm}0.040\) | \(-0.520{\pm}0.041\) | \(\boldsymbol{-}0.512{\pm}0.043\) | \(\boldsymbol{-}0.512{\pm}0.043\) | \(-0.512{\pm}0.042\) |
| monks-2 | (601, 7) | \(-0.491{\pm}0.025\) | \(-0.512{\pm}0.028\) | \(-0.464{\pm}0.031\) | \(\boldsymbol{-}0.442{\pm}0.033\) | \(-0.437{\pm}0.032\) |
| statlog-australian-credit | (690, 15) | \(\boldsymbol{-}0.630{\pm}0.026\) | \(-0.639{\pm}0.036\) | \(\boldsymbol{-}0.630{\pm}0.026\) | \(\boldsymbol{-}0.630{\pm}0.026\) | \(-0.630{\pm}0.025\) |
| credit-approval | (690, 16) | \(\boldsymbol{-}0.342{\pm}0.047\) | \(\boldsymbol{-}0.342{\pm}0.050\) | \(\boldsymbol{-}0.341{\pm}0.052\) | \(-0.342{\pm}0.052\) | \(-0.341{\pm}0.052\) |
| breast-cancer-wisc | (699, 10) | \(\boldsymbol{-}0.094{\pm}0.025\) | \(\boldsymbol{-}0.093{\pm}0.023\) | \(\boldsymbol{-}0.093{\pm}0.029\) | \(-0.093{\pm}0.029\) | \(-0.093{\pm}0.029\) |
| blood | (748, 5) | \(\boldsymbol{-}0.478{\pm}0.039\) | \(\boldsymbol{-}0.479{\pm}0.040\) | \(-0.478{\pm}0.039\) | \(-0.478{\pm}0.039\) | \(-0.478{\pm}0.039\) |
| pima | (768, 9) | \(\boldsymbol{-}0.474{\pm}0.033\) | \(\boldsymbol{-}0.476{\pm}0.038\) | \(\boldsymbol{-}0.474{\pm}0.035\) | \(\boldsymbol{-}0.474{\pm}0.035\) | \(-0.474{\pm}0.035\) |
| mammographic | (961, 6) | \(\boldsymbol{-}0.407{\pm}0.038\) | \(\boldsymbol{-}0.407{\pm}0.040\) | \(\boldsymbol{-}0.408{\pm}0.040\) | \(-0.408{\pm}0.040\) | \(-0.408{\pm}0.040\) |
| statlog-german-credit | (1000, 25) | \(\boldsymbol{-}0.491{\pm}0.030\) | \(\boldsymbol{-}0.491{\pm}0.032\) | \(\boldsymbol{-}0.492{\pm}0.032\) | \(\boldsymbol{-}0.492{\pm}0.032\) | \(-0.492{\pm}0.032\) |
| Bold Count | \(14\) | \(13\) | \(13\) | \(16\) | \(/\) |
5.1 Quality of Marginal Likelihood Approximations↩︎
We compare the quality of marginal likelihood approximations of LA, VI, EP, and our EP-like VI with gold-standard MCMC. We demonstrate this on a binary classification task on the ionosphere data set, with sonar, usps, parkinsons, and monks-2 in 9.2. We estimate the log marginal likelihood on a \(21 \times 21\) grid of values for the log hyperparameters \(\log \boldsymbol{\theta}=(\log \ell, \log \sigma)\) and plot the contour on the grid. For each hyperparameter setting, we fix the hyperparameters and evaluate the approximate log marginal likelihood based on the inferred approximate posterior.
Markov Chain Monte Carlo baseline MCMC is exact in the limit of long runs and thus provides a gold standard for log marginal likelihood estimation. [11] and [12] proposed a sampling scheme based on annealed importance sampling [33] for obtaining a good estimate of the marginal likelihood (see 9.1 for details). The baseline was computed by running \(21 \times 21 =441\) jobs in parallel on a cluster.
Experiment results As shown in the top row of 2 on the ionosphere benchmark data set, the marginal likelihood estimation of EP closely matches the MCMC baseline, whereas that of VI looks clearly different. Notably, when we estimate the marginal likelihood by \(\mathcal{L}_\text{EP}(\boldsymbol{\lambda},\boldsymbol{\theta})\) using the ‘site’ parameters of dual VI (Ours), the contour shapes become much closer to the MCMC result, demonstrating the improvement of using this EP-like marginal likelihood estimation. To investigate whether the improved marginal likelihood estimation also leads to better generalization, we select the optimal hyperparameter location across the grid values and compare the log predictive density on the test set (bottom row of 2). The optimal hyperparameter location of EP-like VI (Ours) is closer to MCMC than VI and generalizes well. We show the same analysis for different data sets covering different types of classification tasks (from general classification to small images) in 9.2, with the same conclusion. In 7 8 9 10, VI and EP conform to their stereotypes of being over- and under-confident, respectively, while Ours tends to have slightly better calibration.
For completeness, and motivated by the seminal work of [11], we provide back-to-back comparisons of both marginal log likelihood and predictive density surfaces also for LA. In 2, the marginal likelihood surface of LA resembles that of VI, while for the predictive density surface VI more closely resembles MCMC compared to LA.
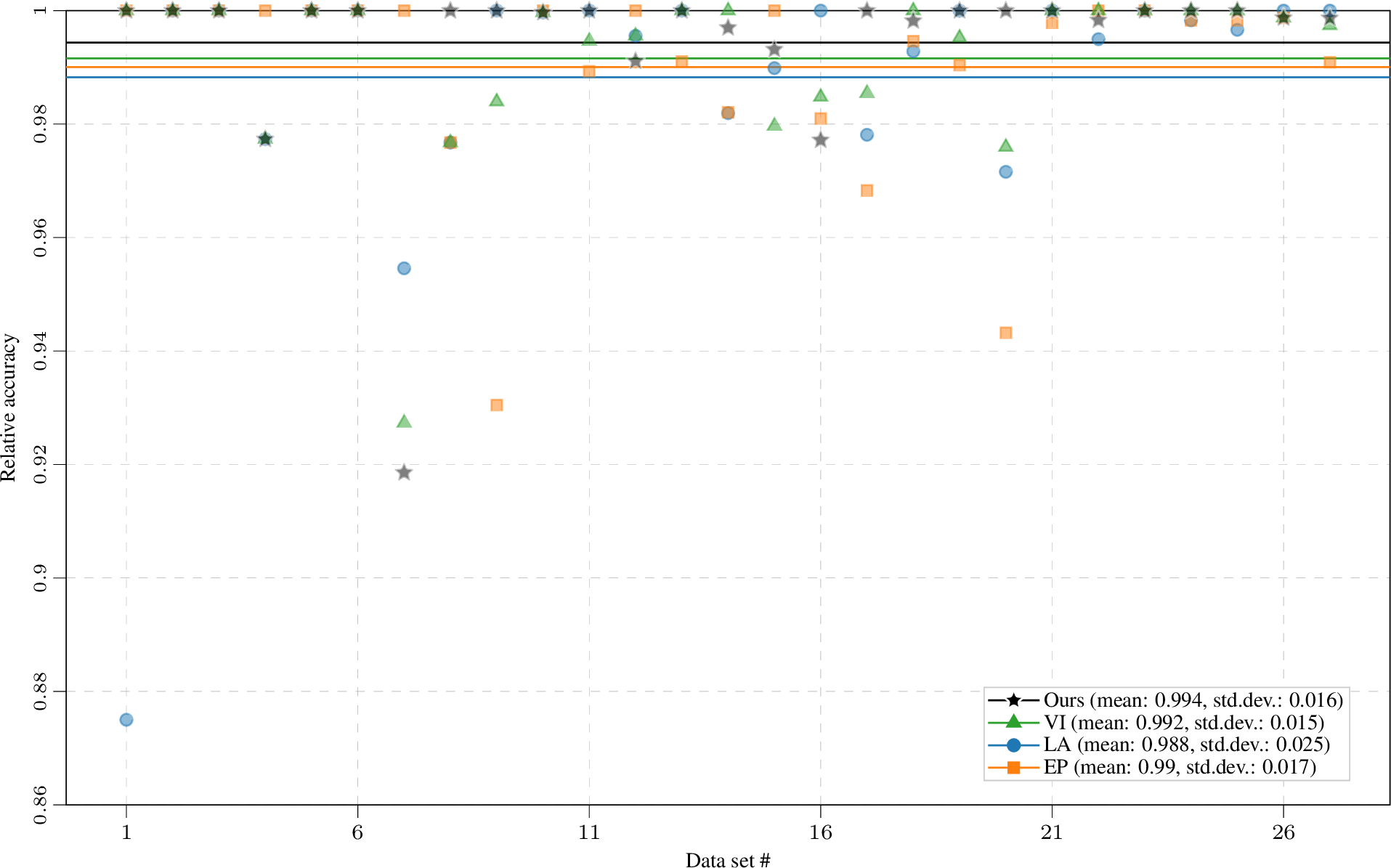
Figure 5: Mean relative accuracy compared to best method on each data set of 1 (over 5-fold CV repeated with 10 seeds). The horizontal lines indicate mean across all data sets; see legend for mean and standard deviation. Our approach yields reliable training, with the highest average relative accuracy and the least outliers.
5.2 Non-Conjugate Tasks in Bayesian Benchmarks↩︎
The log marginal likelihood is a surrogate for the generalization ability of the model to unseen data. To explicitly evaluate the generalization ability of our hybrid training procedure, we compare it against LA, EP, and VI on commonly used benchmark
classification tasks. We use common small and mid-sized data sets (\(n \leq 1000\)) and do full GP inference with 5-fold cross-validation. We use the Bayesian Benchmarks suite (github.com/secondmind-labs/bayesian_benchmarks) for evaluating the methods.
Evaluation on binary classification We consider binary classification with a Bernoulli likelihood on 27 data sets from the UCI repository [34]. For all approximate inference methods, we set the same number of maximum training iterations and use the relative changes in the parameters of the model as convergence criteria. For our hybrid training procedure due to the conflicting objectives in E- and M-steps discussed in 5.5, we use a decrease in the EP learning objective as an additional convergence criterion. As a gold-standard baseline, we include MCMC results. For MCMC, we use a log-uniform hyperpriors to ensure a close match to the model setup in the other models.
To reduce the variance introduced by the training–test set split, we repeat the 5-fold CV with ten different seeds. The performance on the test set is given in 1 and 5. As shown in 1 for log predictive density, LA and EP have very similar performance to VI-based methods (VI and Ours) on most data sets. This empirically demonstrates that for binary classification on small and mid-sized data sets EP and LA generalize well. Our hybrid training procedure achieves the same test performance as VI on most data sets and outperforms VI on three data sets. It empirically demonstrates that when no sparse approximation is required, by using an improved estimation of the marginal likelihood for hyperparameter learning, we could potentially have better generalization ability at no additional computational cost. As the gold standard, MCMC gives the best results; notably, the gap between MCMC and approximate inference methods is relatively small on small data sets. In practice we often favour methods with stable performance over different data sets, i.e., they might not always give the best performance but we can expect consistently good performances. To investigate the reliability of different methods, in 5 we plot the relative accuracy (on each data set we divide the results of each method by the highest accuracy on that data set) for individual data sets and the mean relative accuracy of each method across all data sets. Our approach achieves the most consistent performance on all data sets and thus yields reliable training. We include additional result tables with the same conclusion in 10.3, including experiments with an ARD kernel and checks for initializing other methods with our optimal hyperparameters.
2pt
| (\(n\), \(d\)) | LA | EP | VI | Ours | |||||
|---|---|---|---|---|---|---|---|---|---|
| neal | (100, 1) | \(\boldsymbol{.}317\) | \({\scriptstyle{\pm}.440}\) | \(\boldsymbol{.}303\) | \({\scriptstyle{\pm}.432}\) | \(\boldsymbol{.}295\) | \({\scriptstyle{\pm}.426}\) | \(\boldsymbol{.}301\) | \({\scriptstyle{\pm}.436}\) |
| boston | (506, 13) | \(\boldsymbol{-}.210\) | \({\scriptstyle{\pm}.069}\) | \(\boldsymbol{-}.190\) | \({\scriptstyle{\pm}.053}\) | \(-.206\) | \({\scriptstyle{\pm}.056}\) | \(\boldsymbol{-}.195\) | \({\scriptstyle{\pm}.061}\) |
| stock | (1000, 1) | \(1.910\) | \({\scriptstyle{\pm}.079}\) | \(1.389\) | \({\scriptstyle{\pm}.242}\) | \(1.917\) | \({\scriptstyle{\pm}.082}\) | \(\boldsymbol{1}.921\) | \({\scriptstyle{\pm}.083}\) |
| Bold Count | \(2\) | \(2\) | \(1\) | \(3\) | |||||
5.3 Robust (Student-\(t\)) Regression↩︎
We further test our hybrid training procedure on a more challenging robust regression task with a Student-\(t\) likelihood, a model which is not log-concave. In the likelihood, we fix the degrees of freedom, \(\nu=3\), and only train the noise scale together with hyperparameters. For LA and EP we follow the methods designed by [15]. For VI and our EP-like VI, to make the training procedure numerically stable we crop the gradient w.r.t.the second element of the natural parameters to prevent the approximate posterior covariance from becoming negative. We test on three benchmark data sets previously used for robust regression: the simulated data from [35], the Boston housing regression task, and the stock data from [36]. [15] point out that in Student-\(t\) regression EP provides a good approximation for marginal likelihood and, as shown in 2, by using an EP-like marginal likelihood estimation for hyperparameters learning our hybrid training procedure generalizes better than vanilla VI. The MCMC gold standard results for neal, boston and stock are \(0.309 {\pm} 0.454\), \(-0.191 {\pm} 0.051\), and \(1.586 {\pm} 0.034\), respectively.
5.4 Evaluation under Sparse Approximation↩︎
It is not obvious how a sparse approximation would affect the quality of marginal likelihood approximation. To be able to compare with the MCMC baseline on the full data set, we first analyse the influence of sparsification on ionosphere. We choose 75%, 50%, 25%, and 10% random subsets of training data as inducing points. We estimate the log marginal likelihood as in 5.1 on a grid of values for the log hyperparameters. 4 shows the resulting contour surfaces. Unsurprisingly, as we reduce the number of inducing points, the estimation of the log marginal likelihood becomes less accurate. For moderate sparsification (\(75\%\), \(50\%\)), our EP-like marginal likelihood estimation matches the full MCMC baseline better than VI. For more extreme sparsification, both approximations show significant biases. This is because, with very few inducing points, only larger lengthscales make sense. To match the low-complexity approximation, large lengthscales are required and the ground truth marginal likelihood provided by MCMC becomes irrelevant.
Evaluation on large-scale binary classification We compare LA, EP, VI, and our proposed training procedure on five data sets from 2k to 19k data points (for details, see 11). We use k-means to select 500 inducing points from the input data and keep them fixed. The test set performance is given in 3. Here we are in the regime of \(m/n\) in the range of \(25\%\) to \(2.5\%\), where the log marginal likelihood surface approximations of both VI and our EP-like approximation are likely to be biased away from the true marginal likelihood surface, and the approximate sparse model can no longer be considered a surrogate of the true model.
3pt
| LA | EP | VI | Ours | ||
|---|---|---|---|---|---|
| titanic | \(-.217\scriptstyle{\pm}.037\) | \(-.014\scriptstyle{\pm}.004\) | \(\boldsymbol{-}.011\scriptstyle{\pm}.003\) | \(-.037\scriptstyle{\pm}.005\) | |
| bank | \(\boldsymbol{-}.247\scriptstyle{\pm}.006\) | \(\boldsymbol{-}.246\scriptstyle{\pm}.007\) | \(-.249\scriptstyle{\pm}.006\) | \(-.247\scriptstyle{\pm}.007\) | |
| twonorm | \(\boldsymbol{-}.060\scriptstyle{\pm}.007\) | \(\boldsymbol{-}.061\scriptstyle{\pm}.008\) | \(\boldsymbol{-}.060\scriptstyle{\pm}.008\) | \(-.524\scriptstyle{\pm}.208\) | |
| mushroom | \(-.129\scriptstyle{\pm}.003\) | \(-.002\scriptstyle{\pm}.000\) | \(\boldsymbol{-}.001\scriptstyle{\pm}.000\) | \(-.028\scriptstyle{\pm}.001\) | |
| magic | \(\boldsymbol{-}.285\scriptstyle{\pm}.333\) | \(-.693\scriptstyle{\pm}.000\) | \(\boldsymbol{-}.008\scriptstyle{\pm}.001\) | \(-.070\scriptstyle{\pm}.002\) | |
| Bold Count | \(3\) | \(2\) | \(4\) | \(0\) |
5.5 Practical Considerations↩︎
VEM with the same objective for E- and M-step is analogous to coordinate ascent and hence guaranteed to always improve the objective. With \(\mathcal{L}_\text{VI}\) for E-step and \(\mathcal{L}_\text{EP}\) for M-step, this guarantee no longer holds. This can introduce interplay between the two targets, and in our experiments, we observed that (with certain data-splits/model setups) the optimization can overshoot past the optimum and then becomes increasingly unstable, see 6. In our experiments this conflict between \(\mathcal{L}_\text{E}=\mathcal{L}_\text{VI}\) and \(\mathcal{L}_\text{M}=\mathcal{L}_\text{EP}\) occurred in about 54% of cases. We address this issue by ending optimization once the \(\mathcal{L}_\text{EP}\) objective starts to decrease (see 3). Note that this is solely based on the training data and does not require any additional validation data or tuning per data set.
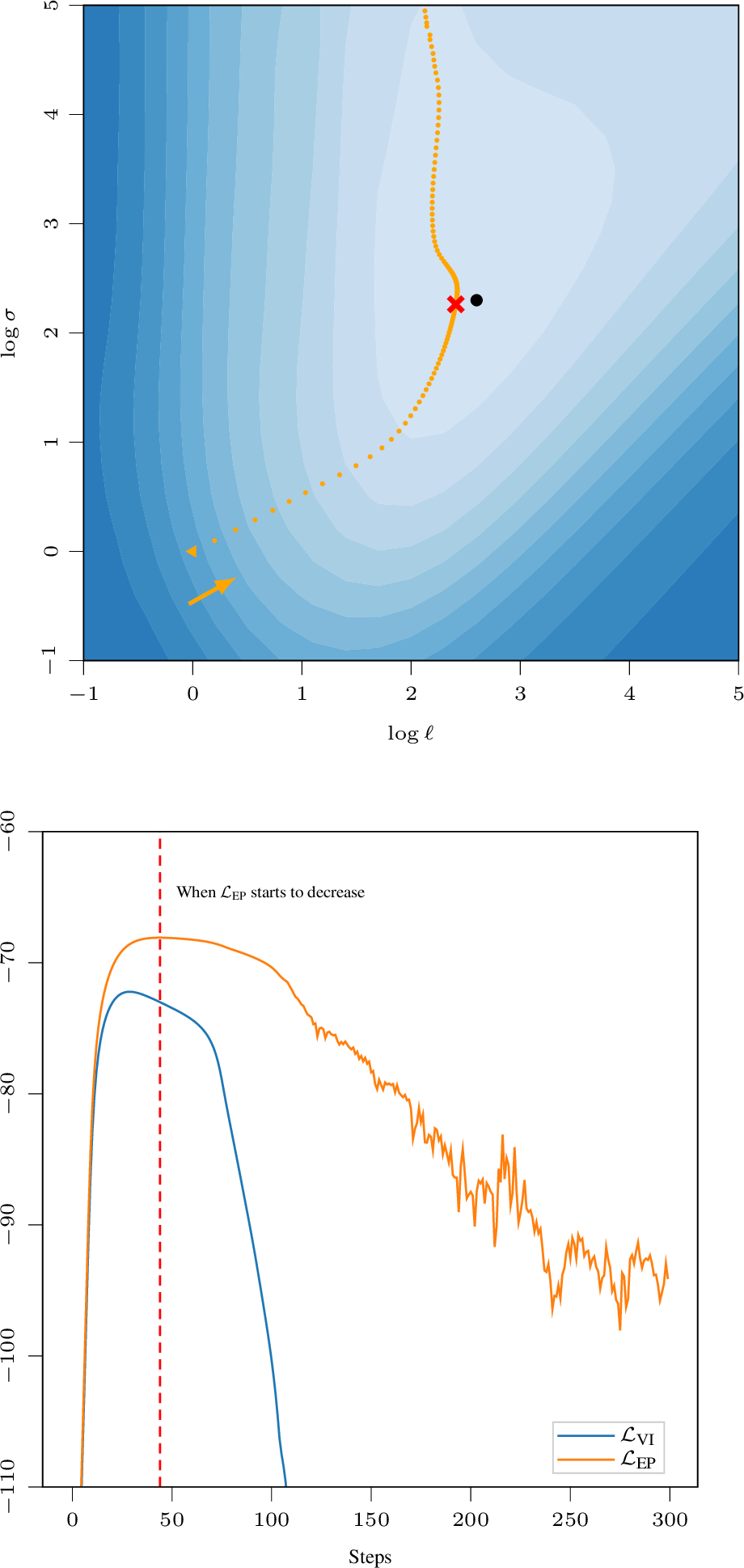
Figure 6: Interplay between the two optimization targets can result in overshooting the optimum ([dot]). The optimizer starts at [triangle] and once it passes [cross] (dashed red; stopping point), \(\mathcal{L}_{\text{EP}}\) starts to decrease. After that, the optimization becomes increasingly unstable.
6 Discussion and Conclusions↩︎
In GP models, the training separates into inference and learning which are typically both cast into an optimization problem. In this paper, we improved hyperparameter learning in non-conjugate GP models by augmenting VI with an EP-like learning target. Our hybrid training procedure builds upon the dual variational GP formulation, introduced by [13] and extended to sparse GPs in [14], which provides a link between VI and EP. We used the representation of the posterior from VI to obtain an EP-like approximation of the marginal likelihood for hyperparameter optimization—without any added computational complexity or computation time.
In the experiments, we evaluated our hybrid training procedure on binary classification tasks and robust regression. For full (non-sparse) models, the extensive results (over 1350 runs per method) show clear benefits in stability, reliability, and performance for our method. This shows the benefits of decoupling inference and learning. When more hyperparameters are present, as shown in 5 and 6 in the appendix, our method has the same performance on log predictive density as VI. However, as shown in 11, our method is still more reliable than VI. For sparse problems, similar empirical benefits could not be demonstrated.
We provide a reference implementation of the methods and code to reproduce the experiments at https://github.com/AaltoML/improved-hyperparameter-learning.
Acknowledgements↩︎
This work was supported by funding from the Academy of Finland (grant id 339730) and the Finnish Center for Artificial Intelligence (FCAI). We acknowledge the computational resources provided by the Aalto Science-IT project and CSC – IT Center for Science, Finland. We thank Aidan Scannell for his constructive comments on the manuscript.
Appendix↩︎
In the supplementary material, we include technical details of the methods that were omitted for brevity in the main paper (7). Additionally, we provide details on the experiments and evaluation setup (8–12) for reproducing the results in the main paper, and include further result tables and figures that extend the evaluation. The codes for the methods proposed in this paper are included as a separate supplement.
7 Method Details↩︎
Sparse energy To extend the presentation in 4, we derive how to obtain the sparse EP marginal likelihood estimation from the VI approximate posterior. Following Eq. (77) in [9], the sites \(t_i(\mathbf{u};\boldsymbol{\zeta}_{\mathbf{u},i})\) in 11 are \[t_i(\mathbf{u};\boldsymbol{\zeta}_{\mathbf{u},i}) \propto \exp \langle\mathbf{u}^{\top} \mathbf{a}_i \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \boldsymbol{\zeta}_{\mathbf{u}, i, 1}-\frac{1}{2} \mathbf{u}^{\top} \mathbf{a}_i \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \mathbf{a}_i^{\top} \mathbf{u}\rangle,\] where \(\mathbf{a}_i=\mathbf{K}_{\mathbf{u}\mathbf{u}}^{-1} \mathbf{k}_{\mathbf{u},i}\), \(\mathbf{K}_{\mathbf{u}\mathbf{u}}= \kappa(\mathbf{Z}, \mathbf{Z})\), and \(\mathbf{k}_{\mathbf{u},i}=\kappa(\mathbf{Z}, \mathbf{x}_i)\) for the \(i\)th data sample. Note that \(\mathbf{u}^{\top} \mathbf{a}_i = \mathbf{a}_i^{\top} \mathbf{u}\) is a scalar.
As \(t_i(\mathbf{u}; \boldsymbol{\lambda}_{\mathbf{u},i})\) in 10 is given by \[\begin{align} t_i(\mathbf{u}; \boldsymbol{\lambda}_{\mathbf{u},i}) &= \exp{\langle\boldsymbol{\lambda}_{\mathbf{u},i}, \mathbf{T}(\mathbf{a}_i^{\top} \mathbf{u})\rangle} \notag\\ &=\exp \langle \boldsymbol{\lambda}_{\mathbf{u},i,1}\mathbf{a}_i^{\top} \mathbf{u}+ \boldsymbol{\lambda}_{\mathbf{u},i,2} (\mathbf{a}_i^{\top} \mathbf{u})^2 \rangle, \end{align}\] we have the following correspondence between \(\boldsymbol{\zeta}_{\mathbf{u}}\) and \(\boldsymbol{\lambda}_{\mathbf{u}}\): \[\label{eq:epviparameter} \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \boldsymbol{\zeta}_{\mathbf{u}, i, 1} \Leftrightarrow \boldsymbol{\lambda}_{\mathbf{u}, i, 1} \qquad \text{and} \qquad -\frac{1}{2}\boldsymbol{\zeta}_{\mathbf{u}, i, 2} \Leftrightarrow \boldsymbol{\lambda}_{\mathbf{u}, i, 2}.\tag{12}\] Following Eq. (126) in [9], the sparse EP energy is (we omit \(\boldsymbol{\theta}\) to make notation simpler) \[\begin{align} \mathcal{L}_{\text{EP}}^\text{sparse}(\boldsymbol{\zeta}_{\mathbf{u}}, \boldsymbol{\theta}) &= \frac{1}{2} \log |\mathbf{S}_{\mathbf{u}}|+\frac{1}{2} \mathbf{m}_{\mathbf{u}}^{\top} \mathbf{S}_{\mathbf{u}}^{-1} \mathbf{m}_{\mathbf{u}}-\frac{1}{2} \log |\mathbf{K}_{\mathbf{u u}}|+\frac{1}{\alpha} \sum_n \log \mathcal{Z}_{\mathrm{tilted}, i} \nonumber\\ &\quad+\sum_n\big[-\frac{1}{2 \alpha} \log (1-\mathbf{a}_i^{\top} \alpha \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \mathbf{S}_{\mathbf{u}} \mathbf{a}_i)+\frac{1}{2} \frac{\mathbf{m}_{\mathbf{u}}^{\top} \mathbf{a}_i \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \mathbf{a}_i^{\top} \mathbf{m}_{\mathbf{u}}}{1-\mathbf{a}_i^{\top} \alpha \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \mathbf{S}_{\mathbf{u}} \mathbf{a}_i} \nonumber\\ &\quad+\frac{1}{2} \boldsymbol{\zeta}_{\mathbf{u}, i, 1} \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \mathbf{a}_i^{\top} \mathbf{V}_{\mathrm{cav}, i} \mathbf{a}_i \alpha \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \boldsymbol{\zeta}_{\mathbf{u}, i, 1}-\boldsymbol{\zeta}_{\mathbf{u}, i, 1} \boldsymbol{\zeta}_{\mathbf{u}, i, 2} \mathbf{a}_i^{\top} \mathbf{V}_{\mathrm{cav}, i}\mathbf{S}_{\mathbf{u}}^{-1} \mathbf{m}_{\mathbf{u}}\big], \label{eq:written95out95sparse95ep95energy} \end{align}\tag{13}\] where the different terms are defined by \[\begin{align} \mathbf{S}_{\mathrm{cav}, i} &= \mathbf{S}_{\mathbf{u}}+\frac{\mathbf{S}_{\mathbf{u}} \mathbf{a}_i \alpha \boldsymbol{\zeta}_{\mathbf{u},i,2} \mathbf{a}_i^{\top} \mathbf{S}_{\mathbf{u}}}{1-\mathbf{a}_i^{\top} \, \alpha \, \boldsymbol{\zeta}_{\mathbf{u},i,2} \mathbf{S}_{\mathbf{u}} \mathbf{a}_i}, \\ \mathbf{S}_{\mathrm{cav}, i}^{-1} \mathbf{m}_{\mathrm{cav}, i}&=\mathbf{S}_{\mathbf{u}}^{-1} \mathbf{m}_{\mathbf{u}}-\alpha \, \mathbf{a}_i \boldsymbol{\zeta}_{\mathbf{u},i,2} \boldsymbol{\zeta}_{\mathbf{u},i,1}, \\ \log \mathcal{Z}_{\mathrm{tilted}, i} &= \log \int q_{\text{cav},i}(f_i) \, p^\alpha\left(y_i \,|\,f_i\right) \,\mathrm{d}f_i, \\ q_{\text{cav},i}(f_i) &= \int p\left(f_i \,|\,\mathbf{u}\right) \mathrm{N}(\mathbf{m}_{\mathrm{cav}, i}, \mathbf{S}_{\mathrm{cav}, i}) \,\mathrm{d}\mathbf{u}. \end{align}\] By substituting \(\boldsymbol{\lambda}_{\mathbf{u},i}\) into \(\boldsymbol{\zeta}_{\mathbf{u},i}\) in 13 using 12 , we obtain the sparse EP marginal likelihood approximation with the VI approximate posterior. When \(\alpha=1\), Power-EP reduces to normal EP, which we use in our experiments.
8 Computational Details↩︎
All experiments ran on a cluster, which allowed us to parallelize jobs. This played a central role especially for the MCMC baseline results for the marginal likelihood surfaces, where we split into 441 separate jobs (per hyperparameter value combination), each of which were allocated 1–3 CPU cores and 1 Gb memory and ran 8–40 h depending on data set size.
9 Quality of Marginal Likelihood Approximation↩︎
Inspired by the work by [11] and [12], we compare the quality of marginal likelihood approximations of LA, VI, EP, and our EP-like VI with a ‘ground’ truth obtained by annealed importance sampling [33]. We demonstrate this on binary classification tasks, where we estimate the log marginal likelihood on a \(21 \times 21\) grid of values for the log hyperparameters \(\log \boldsymbol{\theta}=(\log \ell, \log \sigma)\) and plot the contour on the grid. For each hyperparameter setting, we fix the hyperparameters and evaluate the approximate log marginal likelihood based on the inferred approximate posterior. We then also visualize the log predictive density on hold-out test data as a similar contour plot, showing what the performance of the model would have been if the hyperparameters would have been chosen based on the log marginal likelihood surface in question under the specific inference scheme.
9.1 Markov Chain Monte Carlo Baseline↩︎
As in previous work, we use an MCMC approach as the gold-standard baseline. We use the annealed importance sampling [33] approach from [11] and [12] that defines a sequence of \(t=0,1,\ldots,T\) steps \(Z_t= \int p(\mathbf{y}\,|\,\mathbf{f};\boldsymbol{\theta})^{\tau(t)} p(\mathbf{f};\boldsymbol{\theta})\,\mathrm{d}\mathbf{f}\), where \(\tau(t)=(t/T)^4\) (such that \(\tau(0)=0\) and \(\tau(T)=1\)). The marginal likelihood can be rewritten as \[p(\mathbf{y};\boldsymbol{\theta})=\frac{Z_T}{Z_0}=\frac{Z_T}{Z_{T-1}} \frac{Z_{T-1}}{Z_{T-2}} \cdots \frac{Z_1}{Z_0},\] where \(\frac{Z_t}{Z_{t-1}}\) is approximated by importance sampling using samples from \(q_t(\mathbf{f}) \propto p(\mathbf{y}\,|\,\mathbf{f}; \boldsymbol{\theta})^{\tau(t-1)} \, p(\mathbf{f};\boldsymbol{\theta})\): \[\begin{align} \frac{Z_t}{Z_{t-1}} &= \frac{\int p(\mathbf{y} \,|\,\mathbf{f}; \boldsymbol{\theta})^{\tau(t)} p(\mathbf{f};\boldsymbol{\theta})\,\mathrm{d}\mathbf{f}}{Z_{t-1}} \nonumber \\ &= \int \frac{p(\mathbf{y} \,|\,\mathbf{f}; \boldsymbol{\theta})^{\tau(t)}}{p(\mathbf{y} \,|\,\mathbf{f}; \boldsymbol{\theta})^{\tau(t-1)}} \frac{p(\mathbf{y} \,|\,\mathbf{f}; \boldsymbol{\theta})^{\tau(t-1)}p(\mathbf{f};\boldsymbol{\theta})}{Z_{t-1}} \,\mathrm{d}\mathbf{f}\nonumber \\ & \approx \frac{1}{S} \sum_{s=1}^S p(\mathbf{y} \,|\,\mathbf{f}_t^{(s)}; \boldsymbol{\theta})^{\tau(t)-\tau(t-1)}, \quad \text{where} \quad \mathbf{f}_t^{(s)} \sim \frac{p(\mathbf{y} \,|\,\mathbf{f}; \boldsymbol{\theta})^{\tau(t-1)}p(\mathbf{f};\boldsymbol{\theta})}{Z_{t-1}}. \end{align}\] In practice, instead of sampling \(\mathbf{f}_t\) from \(\frac{p(\mathbf{y} \,|\,\mathbf{f})^{\tau(t-1)}\mathrm{N}(\mathbf{f}\,|\,\mathbf{m}, \mathbf{K})}{Z_{t-1}}\) directly, we use a parameterisation in terms of \(\boldsymbol{\alpha}=\mathbf{K}^{-1}(\mathbf{f}_t-\mathbf{m})\) and sample from \(\boldsymbol{\alpha} \sim P(\boldsymbol{\alpha})=\frac{p(\mathbf{y} \,|\,\mathbf{K}\boldsymbol{\alpha} + \mathbf{m})^{\tau(t-1)}\mathrm{N}(\boldsymbol{\alpha} \,|\,\boldsymbol{0}, \mathbf{K}^{-1})}{Z_a}\) to increase numerical stability since \(\log P(\boldsymbol{\alpha})\) and its gradient can be computed safely. We use elliptical slice sampling [37]. Now, by using a single sample \(S=1\) and a large number of steps \(T\), the estimation of log marginal likelihood can be written as \[\log p(\mathbf{y};\boldsymbol{\theta}) = \sum_{t=1}^{T} \log \frac{Z_t}{Z_{t-1}} \approx \sum_{t=1}^{T} (\tau(t)-\tau(t-1))\log p(\mathbf{y} \,|\,\mathbf{f}_t; \boldsymbol{\theta}).\] Following [11], we set \(T=8000\) and combine three estimates of log marginal likelihood by their geometric mean.
9.2 Experiment Results↩︎
In addition to the figure for the ionosphere data set (2) in the main paper, we include surface plots for four additional data sets in the appendix for more comprehensive comparisons. The marginal likelihood estimation on sonar, usps, parkinsons and monks-2 are given in 7, 8, 9, and 10, respectively. The ionosphere and sonar were included to make it easy to compare to previous work, and the other three chosen as an interesting subset covering different type of classification tasks (from general classification to small images).
Similarly to the results on ionosphere in the main paper, when using the EP-like marginal likelihood estimation from the VI approximate posterior (Ours), the contour shapes become closer to the MCMC result, and the optimal hyperparameter location of EP-like VI (Ours) is closer to MCMC than VI. These effects help explain the quantitative results in the tables in the main paper and the supplement.
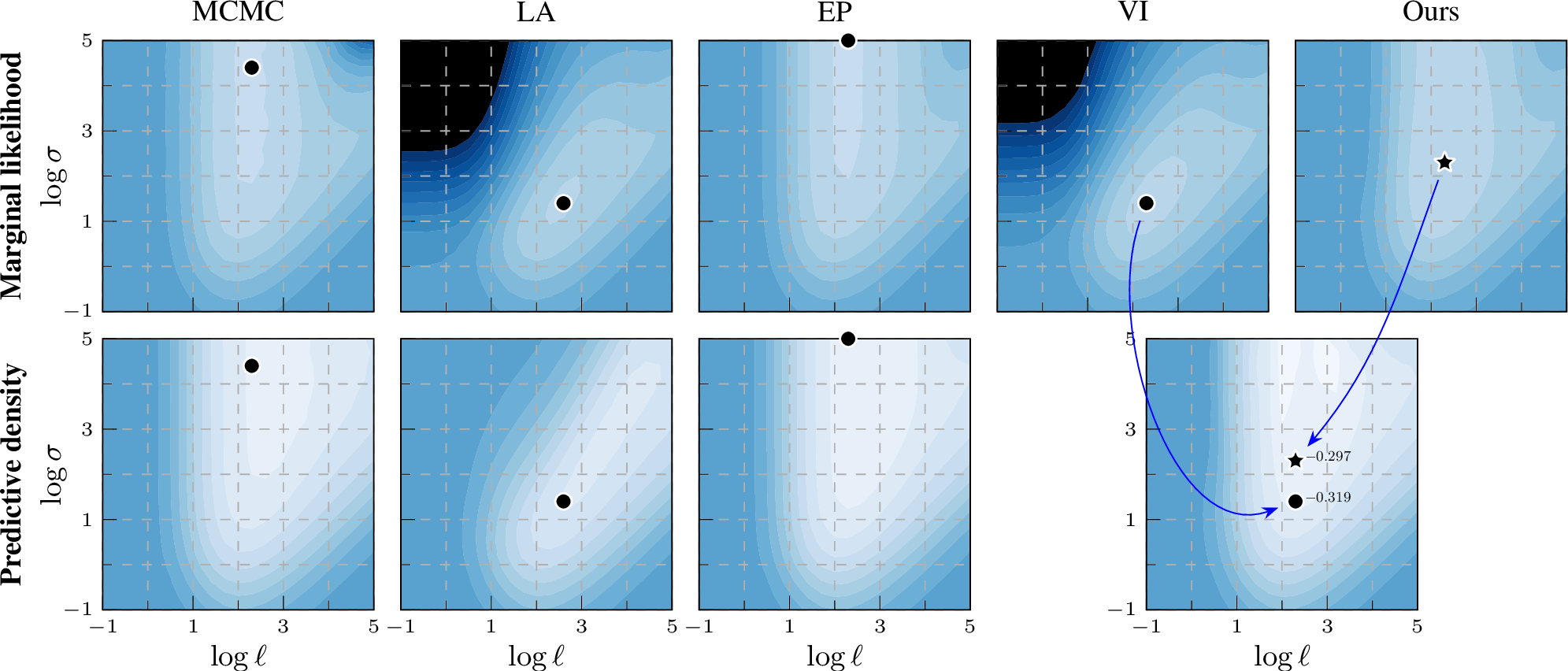
Figure 7: Log marginal likelihood / predictive density surfaces for the sonar data set by varying kernel magnitude \(\sigma\) and lengthscale \(\ell\). The
colour scale is the same in all plots: \(-1.0\)  \(-0.2\) (normalized by \(n\)). Optimal
hyperparameters of each method shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages the same variational
representation as VI.
\(-0.2\) (normalized by \(n\)). Optimal
hyperparameters of each method shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages the same variational
representation as VI.
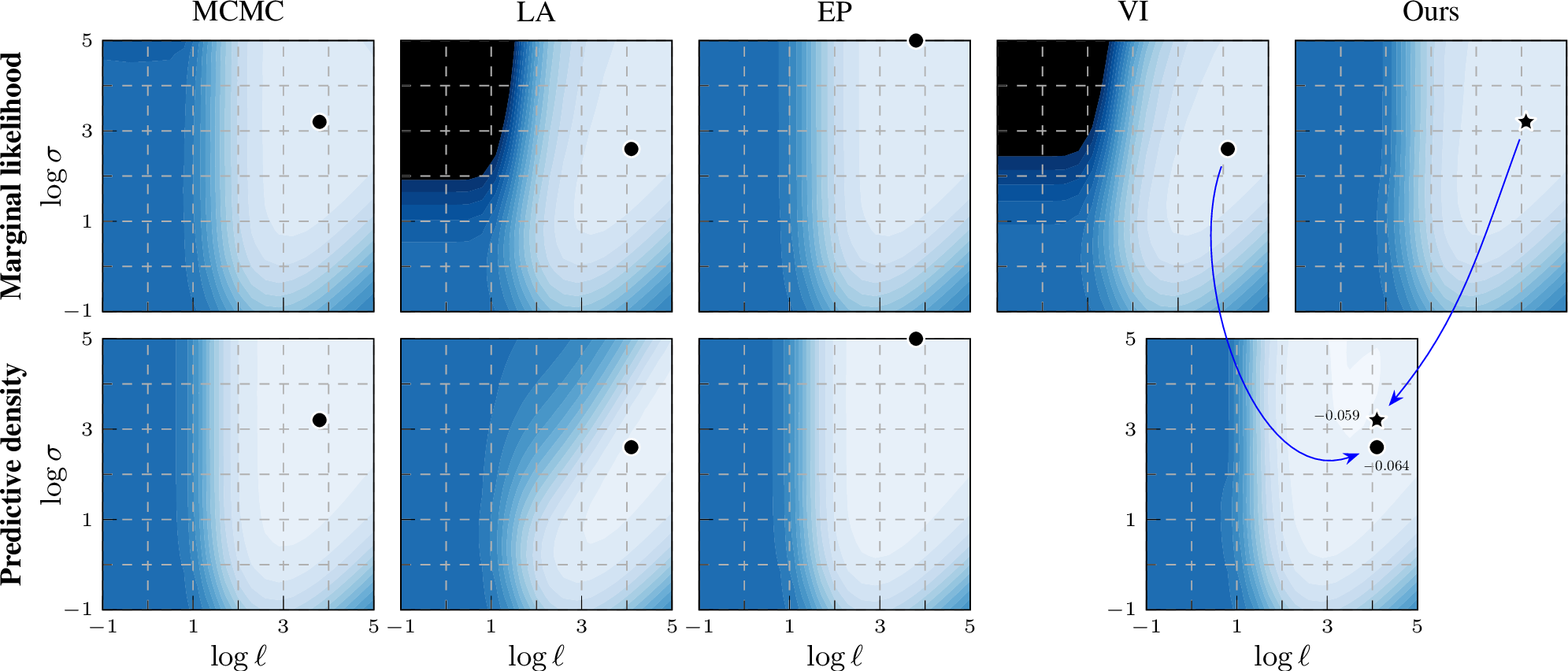
Figure 8: Log marginal likelihood / predictive density surfaces for the usps data set (MNIST-like digits image) by varying kernel magnitude \(\sigma\) and lengthscale \(\ell\). The colour scale is the same in all plots: \(-1.0\)  \(0\) (normalized by \(n\)). Optimal hyperparameters shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages
the same variational representation as VI.
\(0\) (normalized by \(n\)). Optimal hyperparameters shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages
the same variational representation as VI.
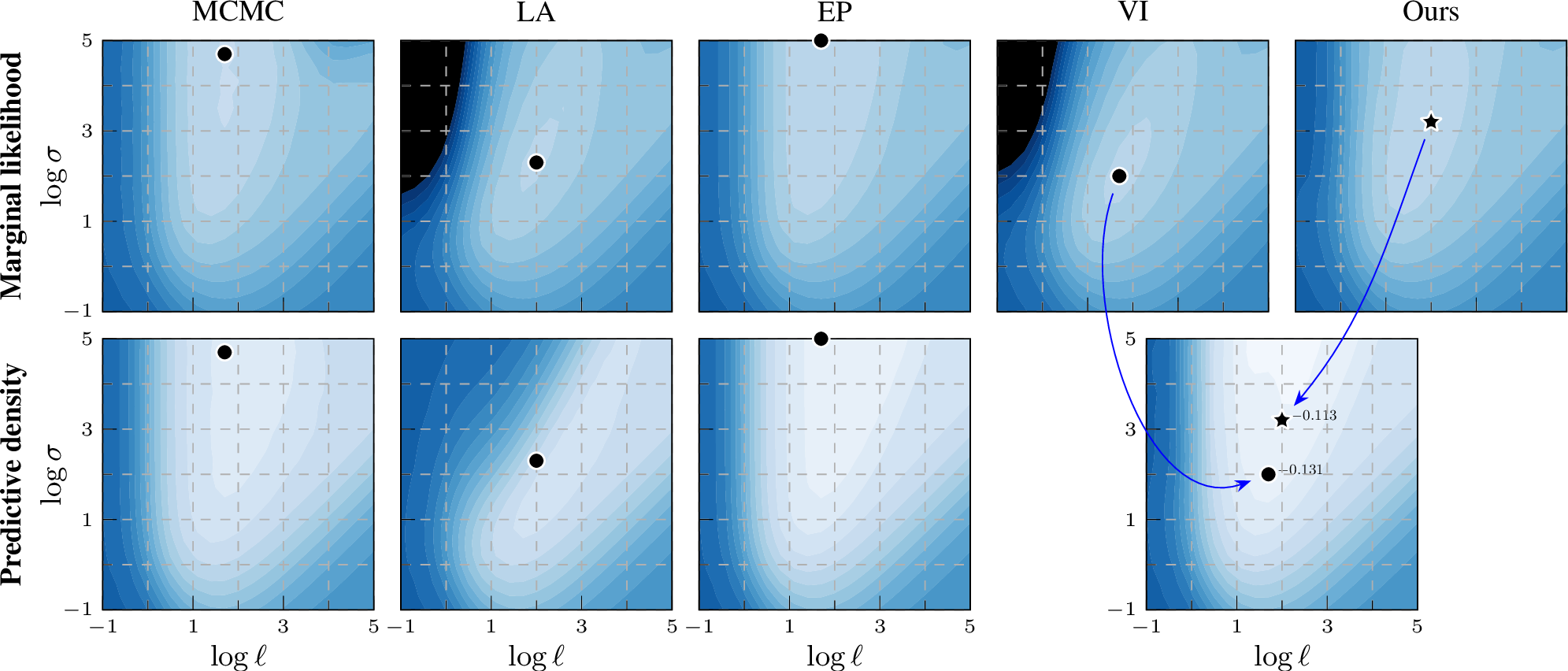
Figure 9: Log marginal likelihood / predictive density surfaces for the parkinsons data set by varying kernel magnitude \(\sigma\) and lengthscale \(\ell\).
The colour scale is the same in all plots: \(-0.8\)  \(0\) (normalized by \(n\)).
Optimal hyperparameters shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages the same variational representation
as VI.
\(0\) (normalized by \(n\)).
Optimal hyperparameters shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages the same variational representation
as VI.
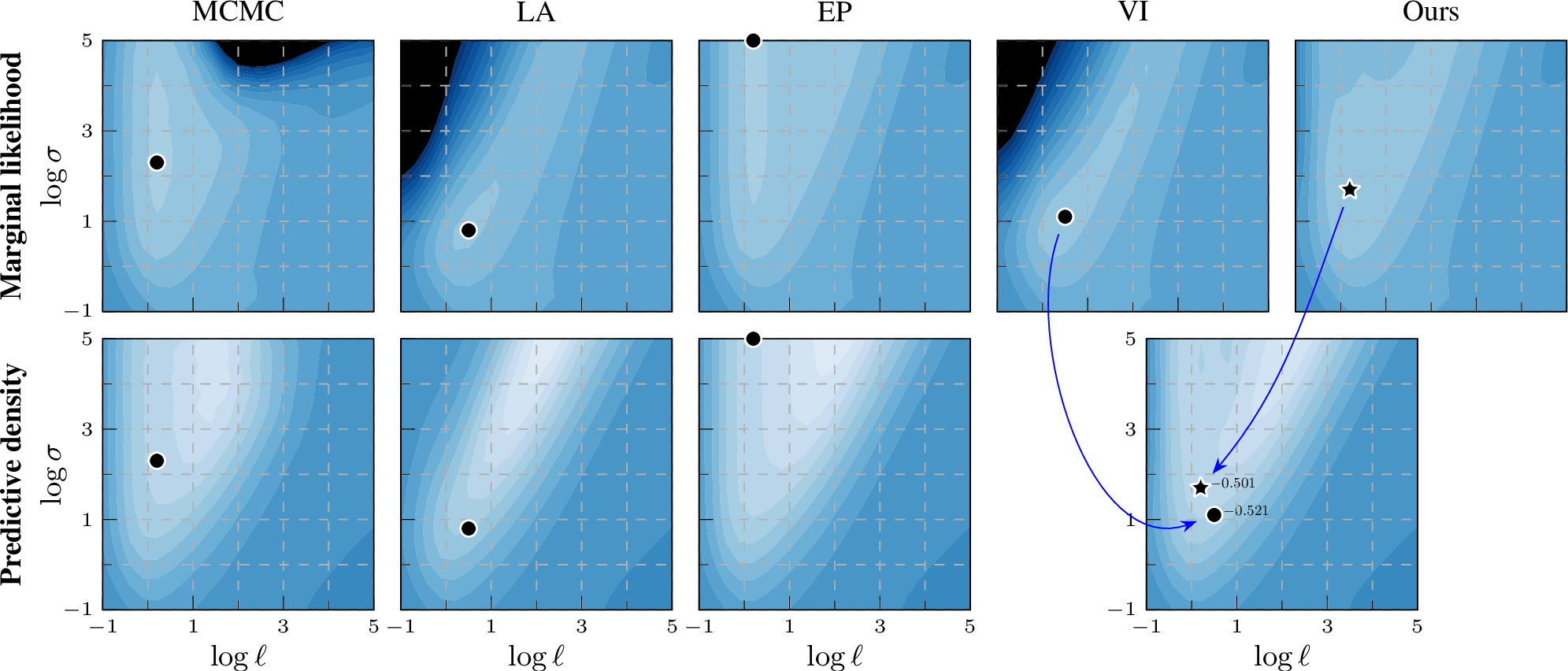
Figure 10: Log marginal likelihood / predictive density surfaces for the monks-2 data set by varying kernel magnitude \(\sigma\) and lengthscale \(\ell\). The
colour scale is the same in all plots: \(-0.9\)  \(-0.3\) (normalized by \(n\)). Optimal
hyperparameters shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages the same variational representation as
VI.
\(-0.3\) (normalized by \(n\)). Optimal
hyperparameters shown by a black marker. EP and our EP-like marginal likelihood estimation match the MCMC baseline better than VI or LA, thus providing a learning proxy. For prediction, our method still leverages the same variational representation as
VI.
10 Non-Conjugate Tasks in Bayesian Benchmarks↩︎
We use the Bayesian Benchmarks suite (github.com/secondmind-labs/bayesian_benchmarks; originally by Salimbeni et al.) for evaluating the methods in binary
classification. Bayesian benchmarks includes common evaluation data sets (typically from UCI) and makes it possible to run a large number of comparisons under a fixed evaluation setup. In the first part, we only include binary classification tasks
(Bernoulli likelihood) with \(n \leq 1000\). We follow the standard setup of input point normalization and splits in the evaluation suite.
10.1 Evaluation Metrics↩︎
We conduct 5-fold cross-validation and use test set accuracy and log predictive density to evaluate the test performance of each method (higher is better in both). To compare different methods, we use the paired \(t\)-test (with \(p=0.05\)) that compares whether the best-performing method performs statistically significantly better than the others.
10.2 Experiment Setup↩︎
We initialize the hyperparameters with unit lengthscale and magnitude for all methods. For LA and EP, the hyperparameters are optimized by the default optimizer L-BFGS-B in GPy. For VI and our hybrid training procedure, each E step and M step consists of 20 iterations. In the E-step we set the learning rate of natural gradient descent to be \(0.1\). In the M-step we use the Adam optimizer [19] with learning rate \(0.01\). We use the convergence criterion described in the main text, with a maximum number of at most \(10\,000\) steps.
For MCMC, we use log uniform prior to ensure it is the same model as the approximate inference methods. We set the burn-in step to be 200, the number of samples to be 10000, and thin the sample with 2.
10.3 Experiment Results↩︎
The test set accuracies are given in 4. For test accuracies all methods achieve similar performance, which is to be expected as accuracy alone only captures where the decision boundary has been draw, completely disregarding second-order information. The log predictive density results are included in the main paper (1). Our hybrid training procedure gives the most consistent results and thus achieves the most reliable training.
10pt
| (\(n\), \(d\)) | LA | EP | VI | Ours | MCMC | |
|---|---|---|---|---|---|---|
| trains | (10, 30) | \(0.620{\pm}0.394\) | \(\boldsymbol{0}.680{\pm}0.371\) | \(0.660{\pm}0.353\) | \(\boldsymbol{0}.710{\pm}0.348\) | \(0.730{\pm}0.349\) |
| balloons | (16, 5) | \(\boldsymbol{0}.618{\pm}0.275\) | \(0.607{\pm}0.282\) | \(\boldsymbol{0}.615{\pm}0.285\) | \(\boldsymbol{0}.650{\pm}0.291\) | \(0.625{\pm}0.272\) |
| fertility | (100, 10) | \(\boldsymbol{0}.879{\pm}0.062\) | \(\boldsymbol{0}.880{\pm}0.062\) | \(\boldsymbol{0}.879{\pm}0.062\) | \(\boldsymbol{0}.877{\pm}0.063\) | \(0.877{\pm}0.061\) |
| pittsburg-bridges-T-OR-D | (102, 8) | \(\boldsymbol{0}.874{\pm}0.070\) | \(\boldsymbol{0}.868{\pm}0.075\) | \(\boldsymbol{0}.875{\pm}0.072\) | \(\boldsymbol{0}.877{\pm}0.068\) | \(0.868{\pm}0.069\) |
| acute-nephritis | (120, 7) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(1.000{\pm}0.000\) |
| acute-inflammation | (120, 7) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(1.000{\pm}0.000\) |
| echocardiogram | (131, 11) | \(0.820{\pm}0.064\) | \(\boldsymbol{0}.840{\pm}0.056\) | \(0.808{\pm}0.069\) | \(0.808{\pm}0.068\) | \(0.797{\pm}0.073\) |
| hepatitis | (155, 20) | \(\boldsymbol{0}.830{\pm}0.059\) | \(0.819{\pm}0.061\) | \(\boldsymbol{0}.833{\pm}0.059\) | \(\boldsymbol{0}.832{\pm}0.060\) | \(0.830{\pm}0.057\) |
| parkinsons | (195, 23) | \(\boldsymbol{0}.951{\pm}0.031\) | \(0.888{\pm}0.050\) | \(0.942{\pm}0.032\) | \(\boldsymbol{0}.949{\pm}0.034\) | \(0.950{\pm}0.031\) |
| breast-cancer-wisc-prog | (198, 34) | \(0.808{\pm}0.058\) | \(0.793{\pm}0.070\) | \(\boldsymbol{0}.815{\pm}0.057\) | \(\boldsymbol{0}.814{\pm}0.057\) | \(0.808{\pm}0.060\) |
| spect | (265, 23) | \(\boldsymbol{0}.706{\pm}0.055\) | \(\boldsymbol{0}.703{\pm}0.057\) | \(\boldsymbol{0}.703{\pm}0.056\) | \(\boldsymbol{0}.705{\pm}0.056\) | \(0.707{\pm}0.058\) |
| statlog-heart | (270, 14) | \(0.830{\pm}0.049\) | \(\boldsymbol{0}.838{\pm}0.047\) | \(0.830{\pm}0.049\) | \(0.828{\pm}0.050\) | \(0.822{\pm}0.050\) |
| haberman-survival | (306, 4) | \(\boldsymbol{0}.741{\pm}0.048\) | \(\boldsymbol{0}.740{\pm}0.050\) | \(\boldsymbol{0}.741{\pm}0.049\) | \(\boldsymbol{0}.741{\pm}0.048\) | \(0.746{\pm}0.047\) |
| ionosphere | (351, 34) | \(0.927{\pm}0.029\) | \(0.930{\pm}0.035\) | \(\boldsymbol{0}.942{\pm}0.030\) | \(\boldsymbol{0}.945{\pm}0.027\) | \(0.943{\pm}0.026\) |
| horse-colic | (368, 26) | \(0.810{\pm}0.042\) | \(\boldsymbol{0}.817{\pm}0.040\) | \(0.805{\pm}0.044\) | \(0.806{\pm}0.043\) | \(0.805{\pm}0.045\) |
| congressional-voting | (435, 17) | \(\boldsymbol{0}.599{\pm}0.046\) | \(\boldsymbol{0}.597{\pm}0.046\) | \(\boldsymbol{0}.598{\pm}0.047\) | \(\boldsymbol{0}.597{\pm}0.049\) | \(0.600{\pm}0.046\) |
| cylinder-bands | (512, 36) | \(0.778{\pm}0.041\) | \(0.763{\pm}0.045\) | \(0.782{\pm}0.041\) | \(\boldsymbol{0}.794{\pm}0.040\) | \(0.795{\pm}0.040\) |
| breast-cancer-wisc-diag | (569, 31) | \(\boldsymbol{0}.969{\pm}0.015\) | \(\boldsymbol{0}.974{\pm}0.015\) | \(\boldsymbol{0}.970{\pm}0.015\) | \(\boldsymbol{0}.972{\pm}0.014\) | \(0.973{\pm}0.016\) |
| ilpd-indian-liver | (583, 10) | \(\boldsymbol{0}.718{\pm}0.035\) | \(\boldsymbol{0}.715{\pm}0.039\) | \(\boldsymbol{0}.719{\pm}0.035\) | \(\boldsymbol{0}.719{\pm}0.035\) | \(0.719{\pm}0.036\) |
| monks-2 | (601, 7) | \(0.758{\pm}0.036\) | \(0.738{\pm}0.034\) | \(0.760{\pm}0.035\) | \(\boldsymbol{0}.773{\pm}0.035\) | \(0.778{\pm}0.034\) |
| statlog-australian-credit | (690, 15) | \(\boldsymbol{0}.677{\pm}0.035\) | \(0.667{\pm}0.032\) | \(\boldsymbol{0}.677{\pm}0.035\) | \(\boldsymbol{0}.677{\pm}0.035\) | \(0.678{\pm}0.035\) |
| credit-approval | (690, 16) | \(\boldsymbol{0}.859{\pm}0.031\) | \(0.856{\pm}0.029\) | \(\boldsymbol{0}.860{\pm}0.030\) | \(\boldsymbol{0}.860{\pm}0.030\) | \(0.859{\pm}0.030\) |
| breast-cancer-wisc | (699, 10) | \(0.967{\pm}0.013\) | \(\boldsymbol{0}.969{\pm}0.012\) | \(0.967{\pm}0.013\) | \(0.967{\pm}0.013\) | \(0.967{\pm}0.013\) |
| blood | (748, 5) | \(\boldsymbol{0}.783{\pm}0.033\) | \(\boldsymbol{0}.784{\pm}0.032\) | \(\boldsymbol{0}.783{\pm}0.034\) | \(\boldsymbol{0}.783{\pm}0.034\) | \(0.779{\pm}0.031\) |
| pima | (768, 9) | \(\boldsymbol{0}.764{\pm}0.030\) | \(\boldsymbol{0}.765{\pm}0.031\) | \(\boldsymbol{0}.764{\pm}0.030\) | \(\boldsymbol{0}.764{\pm}0.030\) | \(0.763{\pm}0.030\) |
| mammographic | (961, 6) | \(\boldsymbol{0}.823{\pm}0.026\) | \(\boldsymbol{0}.823{\pm}0.026\) | \(\boldsymbol{0}.823{\pm}0.026\) | \(\boldsymbol{0}.823{\pm}0.026\) | \(0.823{\pm}0.026\) |
| statlog-german-credit | (1000, 25) | \(\boldsymbol{0}.769{\pm}0.027\) | \(0.766{\pm}0.028\) | \(\boldsymbol{0}.768{\pm}0.027\) | \(\boldsymbol{0}.768{\pm}0.027\) | \(0.767{\pm}0.027\) |
| Bold Count | \(18\) | \(17\) | \(19\) | \(23\) | \(/\) |
10.4 Ablation Studies↩︎
Automatic Relevance Determination Kernel We run experiments with automatic relevance determination (ARD) kernel to see whether our method would perform well when there are multiple hyperparameters. To ensure fair comparison we only include results on data sets where all methods have converged. The log predictive density and test set accuracy are given in 5 and 6 respectively. The mean relative accuracy is plotted in 11. Our training objective performs well overall and achieves reliable training.
10pt
| (\(n\), \(d\)) | LA | EP | VI | Ours | |
|---|---|---|---|---|---|
| fertility | (100, 10) | \(\boldsymbol{-}0.417{\pm}0.096\) | \(\boldsymbol{-}0.407{\pm}0.120\) | \(\boldsymbol{-}0.439{\pm}0.116\) | \(-0.456{\pm}0.115\) |
| pittsburg-bridges-T-OR-D | (102, 8) | \(\boldsymbol{-}0.320{\pm}0.057\) | \(\boldsymbol{-}0.325{\pm}0.085\) | \(\boldsymbol{-}0.325{\pm}0.055\) | \(\boldsymbol{-}0.320{\pm}0.061\) |
| acute-inflammation | (120, 7) | \(-0.112{\pm}0.005\) | \(-0.029{\pm}0.004\) | \(\boldsymbol{-}1.668{\pm}2.754\) | \(\boldsymbol{-}0.005{\pm}0.001\) |
| parkinsons | (195, 23) | \(-0.260{\pm}0.029\) | \(-0.214{\pm}0.086\) | \(\boldsymbol{-}0.062{\pm}0.062\) | \(\boldsymbol{-}0.048{\pm}0.042\) |
| breast-cancer-wisc-prog | (198, 34) | \(\boldsymbol{-}0.498{\pm}0.053\) | \(\boldsymbol{-}0.476{\pm}0.068\) | \(\boldsymbol{-}0.516{\pm}0.080\) | \(\boldsymbol{-}0.644{\pm}0.092\) |
| spect | (265, 23) | \(\boldsymbol{-}0.608{\pm}0.059\) | \(\boldsymbol{-}0.614{\pm}0.064\) | \(\boldsymbol{-}0.643{\pm}0.056\) | \(-0.646{\pm}0.068\) |
| statlog-heart | (270, 14) | \(-0.433{\pm}0.066\) | \(\boldsymbol{-}0.398{\pm}0.056\) | \(-0.450{\pm}0.072\) | \(-0.472{\pm}0.082\) |
| haberman-survival | (306, 4) | \(\boldsymbol{-}0.535{\pm}0.049\) | \(\boldsymbol{-}0.531{\pm}0.053\) | \(\boldsymbol{-}0.539{\pm}0.050\) | \(\boldsymbol{-}0.540{\pm}0.051\) |
| ionosphere | (351, 34) | \(\boldsymbol{-}0.243{\pm}0.058\) | \(\boldsymbol{-}0.253{\pm}0.032\) | \(\boldsymbol{-}0.208{\pm}0.086\) | \(\boldsymbol{-}0.231{\pm}0.061\) |
| congressional-voting | (435, 17) | \(\boldsymbol{-}0.642{\pm}0.030\) | \(\boldsymbol{-}0.639{\pm}0.033\) | \(-0.687{\pm}0.043\) | \(\boldsymbol{-}0.644{\pm}0.081\) |
| cylinder-bands | (512, 36) | \(\boldsymbol{-}0.468{\pm}0.063\) | \(-0.501{\pm}0.061\) | \(\boldsymbol{-}0.454{\pm}0.068\) | \(-0.478{\pm}0.064\) |
| breast-cancer-wisc-diag | (569, 31) | \(\boldsymbol{-}0.098{\pm}0.024\) | \(-0.122{\pm}0.031\) | \(\boldsymbol{-}0.075{\pm}0.044\) | \(\boldsymbol{-}0.073{\pm}0.046\) |
| ilpd-indian-liver | (583, 10) | \(-0.531{\pm}0.030\) | \(\boldsymbol{-}0.518{\pm}0.035\) | \(\boldsymbol{-}0.519{\pm}0.036\) | \(\boldsymbol{-}0.518{\pm}0.037\) |
| monks-2 | (601, 7) | \(-0.458{\pm}0.029\) | \(-0.485{\pm}0.038\) | \(-0.424{\pm}0.037\) | \(\boldsymbol{-}0.399{\pm}0.036\) |
| statlog-australian-credit | (690, 15) | \(\boldsymbol{-}0.633{\pm}0.022\) | \(\boldsymbol{-}0.627{\pm}0.009\) | \(\boldsymbol{-}0.633{\pm}0.022\) | \(\boldsymbol{-}0.632{\pm}0.023\) |
| credit-approval | (690, 16) | \(-0.294{\pm}0.102\) | \(-0.148{\pm}0.015\) | \(\boldsymbol{-}0.905{\pm}1.126\) | \(\boldsymbol{-}0.070{\pm}0.028\) |
| breast-cancer-wisc | (699, 10) | \(\boldsymbol{-}0.102{\pm}0.026\) | \(\boldsymbol{-}0.101{\pm}0.028\) | \(\boldsymbol{-}0.102{\pm}0.034\) | \(\boldsymbol{-}0.104{\pm}0.035\) |
| blood | (748, 5) | \(\boldsymbol{-}0.477{\pm}0.047\) | \(\boldsymbol{-}0.477{\pm}0.049\) | \(\boldsymbol{-}0.477{\pm}0.048\) | \(\boldsymbol{-}0.477{\pm}0.048\) |
| pima | (768, 9) | \(\boldsymbol{-}0.473{\pm}0.034\) | \(\boldsymbol{-}0.466{\pm}0.042\) | \(\boldsymbol{-}0.474{\pm}0.037\) | \(\boldsymbol{-}0.474{\pm}0.036\) |
| mammographic | (961, 6) | \(\boldsymbol{-}0.399{\pm}0.039\) | \(\boldsymbol{-}0.401{\pm}0.041\) | \(\boldsymbol{-}0.400{\pm}0.040\) | \(\boldsymbol{-}0.400{\pm}0.040\) |
| statlog-german-credit | (1000, 25) | \(\boldsymbol{-}0.488{\pm}0.044\) | \(\boldsymbol{-}0.485{\pm}0.046\) | \(-0.501{\pm}0.053\) | \(\boldsymbol{-}0.503{\pm}0.054\) |
| Bold Count | \(15\) | \(15\) | \(17\) | \(17\) |
10pt
| (\(n\), \(d\)) | LA | EP | VI | Ours | |
|---|---|---|---|---|---|
| fertility | (100, 10) | \(\boldsymbol{0}.840{\pm}0.049\) | \(\boldsymbol{0}.880{\pm}0.060\) | \(\boldsymbol{0}.840{\pm}0.049\) | \(\boldsymbol{0}.840{\pm}0.049\) |
| pittsburg-bridges-T-OR-D | (102, 8) | \(\boldsymbol{0}.853{\pm}0.003\) | \(\boldsymbol{0}.863{\pm}0.036\) | \(\boldsymbol{0}.863{\pm}0.019\) | \(\boldsymbol{0}.853{\pm}0.003\) |
| acute-inflammation | (120, 7) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{0}.833{\pm}0.173\) | \(\boldsymbol{1}.000{\pm}0.000\) |
| parkinsons | (195, 23) | \(\boldsymbol{0}.985{\pm}0.021\) | \(\boldsymbol{0}.928{\pm}0.071\) | \(\boldsymbol{0}.990{\pm}0.021\) | \(\boldsymbol{0}.990{\pm}0.021\) |
| breast-cancer-wisc-prog | (198, 34) | \(\boldsymbol{0}.768{\pm}0.029\) | \(\boldsymbol{0}.768{\pm}0.048\) | \(\boldsymbol{0}.773{\pm}0.053\) | \(\boldsymbol{0}.753{\pm}0.049\) |
| spect | (265, 23) | \(\boldsymbol{0}.702{\pm}0.056\) | \(\boldsymbol{0}.709{\pm}0.054\) | \(\boldsymbol{0}.709{\pm}0.057\) | \(\boldsymbol{0}.675{\pm}0.066\) |
| statlog-heart | (270, 14) | \(0.796{\pm}0.039\) | \(\boldsymbol{0}.837{\pm}0.027\) | \(0.789{\pm}0.049\) | \(\boldsymbol{0}.793{\pm}0.054\) |
| haberman-survival | (306, 4) | \(\boldsymbol{0}.732{\pm}0.043\) | \(\boldsymbol{0}.738{\pm}0.038\) | \(\boldsymbol{0}.735{\pm}0.044\) | \(\boldsymbol{0}.735{\pm}0.044\) |
| ionosphere | (351, 34) | \(\boldsymbol{0}.923{\pm}0.026\) | \(\boldsymbol{0}.909{\pm}0.026\) | \(\boldsymbol{0}.932{\pm}0.016\) | \(0.917{\pm}0.016\) |
| congressional-voting | (435, 17) | \(\boldsymbol{0}.607{\pm}0.027\) | \(\boldsymbol{0}.598{\pm}0.030\) | \(\boldsymbol{0}.536{\pm}0.091\) | \(\boldsymbol{0}.607{\pm}0.034\) |
| cylinder-bands | (512, 36) | \(\boldsymbol{0}.791{\pm}0.050\) | \(0.768{\pm}0.043\) | \(\boldsymbol{0}.785{\pm}0.078\) | \(\boldsymbol{0}.799{\pm}0.048\) |
| breast-cancer-wisc-diag | (569, 31) | \(\boldsymbol{0}.975{\pm}0.010\) | \(\boldsymbol{0}.963{\pm}0.022\) | \(\boldsymbol{0}.972{\pm}0.013\) | \(\boldsymbol{0}.974{\pm}0.013\) |
| ilpd-indian-liver | (583, 10) | \(\boldsymbol{0}.707{\pm}0.033\) | \(\boldsymbol{0}.724{\pm}0.033\) | \(0.702{\pm}0.023\) | \(\boldsymbol{0}.705{\pm}0.030\) |
| monks-2 | (601, 7) | \(0.765{\pm}0.040\) | \(0.727{\pm}0.044\) | \(0.769{\pm}0.038\) | \(\boldsymbol{0}.785{\pm}0.031\) |
| statlog-australian-credit | (690, 15) | \(\boldsymbol{0}.651{\pm}0.032\) | \(\boldsymbol{0}.677{\pm}0.018\) | \(\boldsymbol{0}.659{\pm}0.035\) | \(\boldsymbol{0}.649{\pm}0.033\) |
| credit-approval | (690, 16) | \(\boldsymbol{0}.962{\pm}0.020\) | \(0.961{\pm}0.013\) | \(\boldsymbol{0}.859{\pm}0.201\) | \(\boldsymbol{0}.980{\pm}0.011\) |
| breast-cancer-wisc | (699, 10) | \(\boldsymbol{0}.961{\pm}0.011\) | \(\boldsymbol{0}.958{\pm}0.011\) | \(\boldsymbol{0}.964{\pm}0.010\) | \(\boldsymbol{0}.963{\pm}0.012\) |
| blood | (748, 5) | \(\boldsymbol{0}.786{\pm}0.038\) | \(\boldsymbol{0}.789{\pm}0.036\) | \(\boldsymbol{0}.789{\pm}0.036\) | \(\boldsymbol{0}.787{\pm}0.037\) |
| pima | (768, 9) | \(\boldsymbol{0}.766{\pm}0.025\) | \(\boldsymbol{0}.771{\pm}0.028\) | \(\boldsymbol{0}.766{\pm}0.025\) | \(\boldsymbol{0}.767{\pm}0.023\) |
| mammographic | (961, 6) | \(\boldsymbol{0}.831{\pm}0.012\) | \(\boldsymbol{0}.829{\pm}0.016\) | \(\boldsymbol{0}.830{\pm}0.013\) | \(\boldsymbol{0}.830{\pm}0.013\) |
| statlog-german-credit | (1000, 25) | \(\boldsymbol{0}.787{\pm}0.028\) | \(\boldsymbol{0}.779{\pm}0.027\) | \(\boldsymbol{0}.782{\pm}0.028\) | \(\boldsymbol{0}.778{\pm}0.028\) |
| Bold Count | \(19\) | \(18\) | \(18\) | \(20\) |
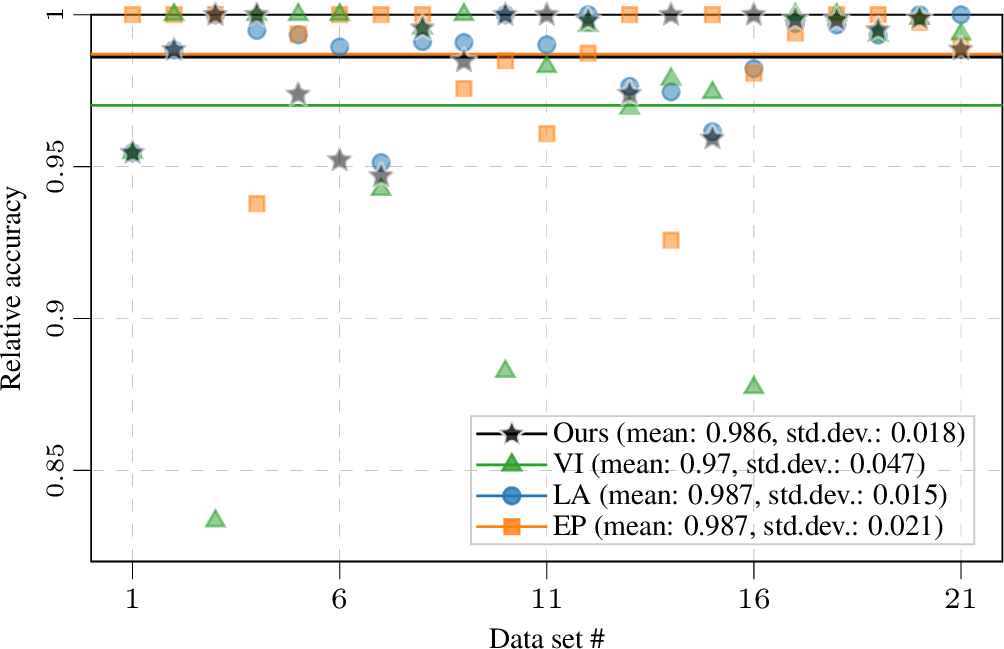
Figure 11: Mean relative accuracy compared to best method on each data set of 6. The horizontal lines indicate mean across all data sets; see legend for mean and standard deviation. Our approach yields reliable training.
Convergence of EP To make sure EP fully converged, we initialized it with the trained hyperparameter values of our method and the log predictive density results and test set accuracies are given in 7 and 8. Compared with 9 and 10, regarding log predictive density EP has three more bolded results and regarding test set accuracies EP has two more bolded results. This underlines some of the issues associated with EP and speaks in favour of our method.
10pt
| (\(n\), \(d\)) | LA | EP (new init.) | VI | Ours | |
|---|---|---|---|---|---|
| trains | (10, 30) | \(\boldsymbol{-}0.695{\pm}0.011\) | \(\boldsymbol{-}0.680{\pm}0.042\) | \(\boldsymbol{-}0.692{\pm}0.023\) | \(\boldsymbol{-}0.681{\pm}0.042\) |
| balloons | (16, 5) | \(\boldsymbol{-}0.707{\pm}0.146\) | \(\boldsymbol{-}0.672{\pm}0.263\) | \(\boldsymbol{-}0.711{\pm}0.239\) | \(\boldsymbol{-}0.657{\pm}0.267\) |
| fertility | (100, 10) | \(\boldsymbol{-}0.379{\pm}0.099\) | \(\boldsymbol{-}0.379{\pm}0.103\) | \(\boldsymbol{-}0.378{\pm}0.103\) | \(\boldsymbol{-}0.379{\pm}0.103\) |
| pittsburg-bridges-T-OR-D | (102, 8) | \(\boldsymbol{-}0.306{\pm}0.044\) | \(\boldsymbol{-}0.295{\pm}0.058\) | \(\boldsymbol{-}0.295{\pm}0.057\) | \(\boldsymbol{-}0.296{\pm}0.059\) |
| acute-nephritis | (120, 7) | \(-0.203{\pm}0.010\) | \(-0.010{\pm}0.003\) | \(-0.006{\pm}0.002\) | \(\boldsymbol{-}0.005{\pm}0.001\) |
| acute-inflammation | (120, 7) | \(-0.172{\pm}0.033\) | \(-0.013{\pm}0.002\) | \(-0.008{\pm}0.001\) | \(\boldsymbol{-}0.007{\pm}0.001\) |
| echocardiogram | (131, 11) | \(\boldsymbol{-}0.420{\pm}0.073\) | \(\boldsymbol{-}0.421{\pm}0.086\) | \(\boldsymbol{-}0.420{\pm}0.085\) | \(\boldsymbol{-}0.421{\pm}0.086\) |
| hepatitis | (155, 20) | \(\boldsymbol{-}0.369{\pm}0.043\) | \(\boldsymbol{-}0.362{\pm}0.052\) | \(\boldsymbol{-}0.361{\pm}0.051\) | \(\boldsymbol{-}0.361{\pm}0.052\) |
| parkinsons | (195, 23) | \(-0.267{\pm}0.030\) | \(-0.153{\pm}0.050\) | \(-0.164{\pm}0.062\) | \(\boldsymbol{-}0.145{\pm}0.054\) |
| breast-cancer-wisc-prog | (198, 34) | \(\boldsymbol{-}0.460{\pm}0.063\) | \(\boldsymbol{-}0.458{\pm}0.070\) | \(\boldsymbol{-}0.458{\pm}0.071\) | \(\boldsymbol{-}0.458{\pm}0.070\) |
| spect | (265, 23) | \(\boldsymbol{-}0.587{\pm}0.045\) | \(\boldsymbol{-}0.590{\pm}0.051\) | \(\boldsymbol{-}0.589{\pm}0.050\) | \(\boldsymbol{-}0.590{\pm}0.051\) |
| statlog-heart | (270, 14) | \(\boldsymbol{-}0.392{\pm}0.071\) | \(\boldsymbol{-}0.395{\pm}0.080\) | \(\boldsymbol{-}0.394{\pm}0.080\) | \(\boldsymbol{-}0.395{\pm}0.080\) |
| haberman-survival | (306, 4) | \(\boldsymbol{-}0.535{\pm}0.050\) | \(\boldsymbol{-}0.537{\pm}0.054\) | \(\boldsymbol{-}0.537{\pm}0.054\) | \(\boldsymbol{-}0.537{\pm}0.054\) |
| ionosphere | (351, 34) | \(-0.221{\pm}0.021\) | \(-0.173{\pm}0.031\) | \(\boldsymbol{-}0.169{\pm}0.031\) | \(\boldsymbol{-}0.169{\pm}0.033\) |
| horse-colic | (368, 26) | \(\boldsymbol{-}0.465{\pm}0.058\) | \(\boldsymbol{-}0.469{\pm}0.068\) | \(\boldsymbol{-}0.466{\pm}0.068\) | \(\boldsymbol{-}0.469{\pm}0.068\) |
| congressional-voting | (435, 17) | \(\boldsymbol{-}0.636{\pm}0.026\) | \(\boldsymbol{-}0.636{\pm}0.029\) | \(\boldsymbol{-}0.636{\pm}0.029\) | \(\boldsymbol{-}0.636{\pm}0.029\) |
| cylinder-bands | (512, 36) | \(-0.482{\pm}0.030\) | \(\boldsymbol{-}0.442{\pm}0.038\) | \(-0.457{\pm}0.038\) | \(\boldsymbol{-}0.441{\pm}0.040\) |
| breast-cancer-wisc-diag | (569, 31) | \(\boldsymbol{-}0.079{\pm}0.020\) | \(\boldsymbol{-}0.069{\pm}0.040\) | \(\boldsymbol{-}0.071{\pm}0.038\) | \(\boldsymbol{-}0.071{\pm}0.045\) |
| ilpd-indian-liver | (583, 10) | \(\boldsymbol{-}0.516{\pm}0.033\) | \(\boldsymbol{-}0.516{\pm}0.037\) | \(\boldsymbol{-}0.516{\pm}0.037\) | \(\boldsymbol{-}0.516{\pm}0.037\) |
| monks-2 | (601, 7) | \(-0.496{\pm}0.037\) | \(\boldsymbol{-}0.445{\pm}0.042\) | \(-0.468{\pm}0.045\) | \(\boldsymbol{-}0.443{\pm}0.044\) |
| statlog-australian-credit | (690, 15) | \(\boldsymbol{-}0.627{\pm}0.022\) | \(\boldsymbol{-}0.627{\pm}0.023\) | \(\boldsymbol{-}0.627{\pm}0.023\) | \(\boldsymbol{-}0.627{\pm}0.023\) |
| credit-approval | (690, 16) | \(\boldsymbol{-}0.342{\pm}0.008\) | \(\boldsymbol{-}0.341{\pm}0.009\) | \(\boldsymbol{-}0.341{\pm}0.008\) | \(\boldsymbol{-}0.341{\pm}0.009\) |
| breast-cancer-wisc | (699, 10) | \(\boldsymbol{-}0.091{\pm}0.030\) | \(\boldsymbol{-}0.091{\pm}0.037\) | \(\boldsymbol{-}0.091{\pm}0.037\) | \(\boldsymbol{-}0.091{\pm}0.037\) |
| blood | (748, 5) | \(\boldsymbol{-}0.475{\pm}0.043\) | \(\boldsymbol{-}0.476{\pm}0.044\) | \(\boldsymbol{-}0.476{\pm}0.044\) | \(\boldsymbol{-}0.476{\pm}0.044\) |
| pima | (768, 9) | \(\boldsymbol{-}0.470{\pm}0.031\) | \(\boldsymbol{-}0.471{\pm}0.033\) | \(\boldsymbol{-}0.471{\pm}0.033\) | \(\boldsymbol{-}0.471{\pm}0.033\) |
| mammographic | (961, 6) | \(\boldsymbol{-}0.408{\pm}0.037\) | \(\boldsymbol{-}0.408{\pm}0.039\) | \(\boldsymbol{-}0.408{\pm}0.039\) | \(\boldsymbol{-}0.408{\pm}0.039\) |
| statlog-german-credit | (1000, 25) | \(\boldsymbol{-}0.493{\pm}0.040\) | \(\boldsymbol{-}0.494{\pm}0.043\) | \(\boldsymbol{-}0.493{\pm}0.043\) | \(\boldsymbol{-}0.494{\pm}0.043\) |
| Bold Count | \(21\) | \(23\) | \(22\) | \(27\) |
10pt
| (\(n\), \(d\)) | LA | EP (new init.) | VI | Ours | |
|---|---|---|---|---|---|
| trains | (10, 30) | \(\boldsymbol{0}.700{\pm}0.400\) | \(\boldsymbol{0}.800{\pm}0.245\) | \(\boldsymbol{0}.800{\pm}0.245\) | \(\boldsymbol{0}.800{\pm}0.245\) |
| balloons | (16, 5) | \(\boldsymbol{0}.667{\pm}0.298\) | \(\boldsymbol{0}.667{\pm}0.298\) | \(\boldsymbol{0}.667{\pm}0.298\) | \(\boldsymbol{0}.667{\pm}0.298\) |
| fertility | (100, 10) | \(\boldsymbol{0}.880{\pm}0.060\) | \(\boldsymbol{0}.880{\pm}0.060\) | \(\boldsymbol{0}.880{\pm}0.060\) | \(\boldsymbol{0}.880{\pm}0.060\) |
| pittsburg-bridges-T-OR-D | (102, 8) | \(\boldsymbol{0}.863{\pm}0.036\) | \(\boldsymbol{0}.863{\pm}0.036\) | \(\boldsymbol{0}.863{\pm}0.036\) | \(\boldsymbol{0}.863{\pm}0.036\) |
| acute-nephritis | (120, 7) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) |
| acute-inflammation | (120, 7) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) |
| echocardiogram | (131, 11) | \(\boldsymbol{0}.808{\pm}0.061\) | \(\boldsymbol{0}.778{\pm}0.063\) | \(\boldsymbol{0}.785{\pm}0.076\) | \(\boldsymbol{0}.778{\pm}0.063\) |
| hepatitis | (155, 20) | \(\boldsymbol{0}.813{\pm}0.024\) | \(\boldsymbol{0}.832{\pm}0.024\) | \(\boldsymbol{0}.813{\pm}0.024\) | \(\boldsymbol{0}.832{\pm}0.024\) |
| parkinsons | (195, 23) | \(\boldsymbol{0}.959{\pm}0.048\) | \(\boldsymbol{0}.959{\pm}0.048\) | \(\boldsymbol{0}.944{\pm}0.050\) | \(\boldsymbol{0}.959{\pm}0.048\) |
| breast-cancer-wisc-prog | (198, 34) | \(\boldsymbol{0}.793{\pm}0.051\) | \(\boldsymbol{0}.793{\pm}0.051\) | \(\boldsymbol{0}.793{\pm}0.051\) | \(\boldsymbol{0}.793{\pm}0.051\) |
| spect | (265, 23) | \(\boldsymbol{0}.706{\pm}0.031\) | \(\boldsymbol{0}.706{\pm}0.023\) | \(\boldsymbol{0}.702{\pm}0.028\) | \(\boldsymbol{0}.706{\pm}0.023\) |
| statlog-heart | (270, 14) | \(\boldsymbol{0}.830{\pm}0.036\) | \(\boldsymbol{0}.826{\pm}0.034\) | \(\boldsymbol{0}.830{\pm}0.036\) | \(\boldsymbol{0}.826{\pm}0.034\) |
| haberman-survival | (306, 4) | \(\boldsymbol{0}.725{\pm}0.039\) | \(\boldsymbol{0}.725{\pm}0.039\) | \(\boldsymbol{0}.725{\pm}0.039\) | \(\boldsymbol{0}.725{\pm}0.039\) |
| ionosphere | (351, 34) | \(\boldsymbol{0}.932{\pm}0.025\) | \(\boldsymbol{0}.946{\pm}0.028\) | \(\boldsymbol{0}.949{\pm}0.026\) | \(\boldsymbol{0}.946{\pm}0.028\) |
| horse-colic | (368, 26) | \(\boldsymbol{0}.799{\pm}0.035\) | \(\boldsymbol{0}.802{\pm}0.039\) | \(0.791{\pm}0.045\) | \(\boldsymbol{0}.802{\pm}0.039\) |
| congressional-voting | (435, 17) | \(\boldsymbol{0}.605{\pm}0.024\) | \(\boldsymbol{0}.591{\pm}0.016\) | \(\boldsymbol{0}.595{\pm}0.013\) | \(\boldsymbol{0}.591{\pm}0.016\) |
| cylinder-bands | (512, 36) | \(0.785{\pm}0.037\) | \(\boldsymbol{0}.803{\pm}0.030\) | \(\boldsymbol{0}.791{\pm}0.034\) | \(\boldsymbol{0}.803{\pm}0.031\) |
| breast-cancer-wisc-diag | (569, 31) | \(0.972{\pm}0.010\) | \(\boldsymbol{0}.975{\pm}0.009\) | \(\boldsymbol{0}.979{\pm}0.009\) | \(\boldsymbol{0}.977{\pm}0.011\) |
| ilpd-indian-liver | (583, 10) | \(\boldsymbol{0}.719{\pm}0.025\) | \(\boldsymbol{0}.719{\pm}0.028\) | \(\boldsymbol{0}.715{\pm}0.027\) | \(\boldsymbol{0}.719{\pm}0.028\) |
| monks-2 | (601, 7) | \(\boldsymbol{0}.740{\pm}0.049\) | \(\boldsymbol{0}.762{\pm}0.045\) | \(\boldsymbol{0}.744{\pm}0.046\) | \(\boldsymbol{0}.762{\pm}0.045\) |
| statlog-australian-credit | (690, 15) | \(\boldsymbol{0}.678{\pm}0.028\) | \(\boldsymbol{0}.678{\pm}0.028\) | \(\boldsymbol{0}.678{\pm}0.028\) | \(\boldsymbol{0}.678{\pm}0.028\) |
| credit-approval | (690, 16) | \(\boldsymbol{0}.859{\pm}0.026\) | \(\boldsymbol{0}.862{\pm}0.026\) | \(\boldsymbol{0}.864{\pm}0.024\) | \(\boldsymbol{0}.862{\pm}0.026\) |
| breast-cancer-wisc | (699, 10) | \(\boldsymbol{0}.969{\pm}0.016\) | \(\boldsymbol{0}.969{\pm}0.016\) | \(\boldsymbol{0}.969{\pm}0.016\) | \(\boldsymbol{0}.969{\pm}0.016\) |
| blood | (748, 5) | \(\boldsymbol{0}.785{\pm}0.042\) | \(\boldsymbol{0}.786{\pm}0.044\) | \(\boldsymbol{0}.786{\pm}0.044\) | \(\boldsymbol{0}.786{\pm}0.044\) |
| pima | (768, 9) | \(\boldsymbol{0}.764{\pm}0.027\) | \(\boldsymbol{0}.767{\pm}0.026\) | \(\boldsymbol{0}.767{\pm}0.026\) | \(\boldsymbol{0}.767{\pm}0.026\) |
| mammographic | (961, 6) | \(\boldsymbol{0}.824{\pm}0.019\) | \(\boldsymbol{0}.823{\pm}0.019\) | \(\boldsymbol{0}.823{\pm}0.019\) | \(\boldsymbol{0}.823{\pm}0.019\) |
| statlog-german-credit | (1000, 25) | \(\boldsymbol{0}.770{\pm}0.039\) | \(\boldsymbol{0}.769{\pm}0.037\) | \(\boldsymbol{0}.768{\pm}0.038\) | \(\boldsymbol{0}.769{\pm}0.037\) |
| Bold Count | \(25\) | \(27\) | \(26\) | \(27\) |
10pt
| # | (\(n\), \(d\)) | LA | EP | VI | Ours | |
|---|---|---|---|---|---|---|
| 1 | trains | (10, 30) | \(\boldsymbol{-}0.695{\pm}0.011\) | \(\boldsymbol{-}0.687{\pm}0.023\) | \(\boldsymbol{-}0.692{\pm}0.023\) | \(\boldsymbol{-}0.681{\pm}0.042\) |
| 2 | balloons | (16, 5) | \(\boldsymbol{-}0.707{\pm}0.146\) | \(\boldsymbol{-}0.684{\pm}0.161\) | \(\boldsymbol{-}0.711{\pm}0.239\) | \(\boldsymbol{-}0.657{\pm}0.267\) |
| 3 | fertility | (100, 10) | \(\boldsymbol{-}0.379{\pm}0.099\) | \(\boldsymbol{-}0.384{\pm}0.138\) | \(\boldsymbol{-}0.378{\pm}0.103\) | \(\boldsymbol{-}0.379{\pm}0.103\) |
| 4 | pittsburg-bridges-T-OR-D | (102, 8) | \(\boldsymbol{-}0.306{\pm}0.044\) | \(\boldsymbol{-}0.316{\pm}0.060\) | \(\boldsymbol{-}0.295{\pm}0.057\) | \(\boldsymbol{-}0.296{\pm}0.059\) |
| 5 | acute-nephritis | (120, 7) | \(-0.203{\pm}0.010\) | \(-0.047{\pm}0.009\) | \(-0.006{\pm}0.002\) | \(\boldsymbol{-}0.005{\pm}0.001\) |
| 6 | acute-inflammation | (120, 7) | \(-0.172{\pm}0.033\) | \(-0.055{\pm}0.005\) | \(-0.008{\pm}0.001\) | \(\boldsymbol{-}0.007{\pm}0.001\) |
| 7 | echocardiogram | (131, 11) | \(\boldsymbol{-}0.420{\pm}0.073\) | \(\boldsymbol{-}0.412{\pm}0.084\) | \(\boldsymbol{-}0.420{\pm}0.085\) | \(\boldsymbol{-}0.421{\pm}0.086\) |
| 8 | hepatitis | (155, 20) | \(\boldsymbol{-}0.369{\pm}0.043\) | \(\boldsymbol{-}0.376{\pm}0.046\) | \(\boldsymbol{-}0.361{\pm}0.051\) | \(\boldsymbol{-}0.361{\pm}0.052\) |
| 9 | parkinsons | (195, 23) | \(-0.267{\pm}0.030\) | \(-0.302{\pm}0.090\) | \(-0.164{\pm}0.062\) | \(\boldsymbol{-}0.145{\pm}0.054\) |
| 10 | breast-cancer-wisc-prog | (198, 34) | \(\boldsymbol{-}0.460{\pm}0.063\) | \(\boldsymbol{-}0.478{\pm}0.083\) | \(\boldsymbol{-}0.458{\pm}0.071\) | \(\boldsymbol{-}0.458{\pm}0.070\) |
| 11 | spect | (265, 23) | \(\boldsymbol{-}0.587{\pm}0.045\) | \(\boldsymbol{-}0.587{\pm}0.052\) | \(\boldsymbol{-}0.589{\pm}0.050\) | \(\boldsymbol{-}0.590{\pm}0.051\) |
| 12 | statlog-heart | (270, 14) | \(\boldsymbol{-}0.392{\pm}0.071\) | \(\boldsymbol{-}0.380{\pm}0.058\) | \(\boldsymbol{-}0.394{\pm}0.080\) | \(\boldsymbol{-}0.395{\pm}0.080\) |
| 13 | haberman-survival | (306, 4) | \(\boldsymbol{-}0.535{\pm}0.050\) | \(\boldsymbol{-}0.539{\pm}0.059\) | \(\boldsymbol{-}0.537{\pm}0.054\) | \(\boldsymbol{-}0.537{\pm}0.054\) |
| 14 | ionosphere | (351, 34) | \(-0.221{\pm}0.021\) | \(-0.227{\pm}0.016\) | \(\boldsymbol{-}0.169{\pm}0.031\) | \(\boldsymbol{-}0.169{\pm}0.033\) |
| 15 | horse-colic | (368, 26) | \(-0.465{\pm}0.058\) | \(\boldsymbol{-}0.455{\pm}0.060\) | \(\boldsymbol{-}0.466{\pm}0.068\) | \(\boldsymbol{-}0.469{\pm}0.068\) |
| 16 | congressional-voting | (435, 17) | \(\boldsymbol{-}0.636{\pm}0.026\) | \(\boldsymbol{-}0.633{\pm}0.027\) | \(\boldsymbol{-}0.636{\pm}0.029\) | \(\boldsymbol{-}0.636{\pm}0.029\) |
| 17 | cylinder-bands | (512, 36) | \(-0.482{\pm}0.030\) | \(-0.495{\pm}0.030\) | \(-0.457{\pm}0.038\) | \(\boldsymbol{-}0.441{\pm}0.040\) |
| 18 | breast-cancer-wisc-diag | (569, 31) | \(\boldsymbol{-}0.079{\pm}0.020\) | \(-0.140{\pm}0.015\) | \(\boldsymbol{-}0.071{\pm}0.038\) | \(\boldsymbol{-}0.071{\pm}0.045\) |
| 19 | ilpd-indian-liver | (583, 10) | \(\boldsymbol{-}0.516{\pm}0.033\) | \(\boldsymbol{-}0.521{\pm}0.033\) | \(\boldsymbol{-}0.516{\pm}0.037\) | \(\boldsymbol{-}0.516{\pm}0.037\) |
| 20 | monks-2 | (601, 7) | \(-0.496{\pm}0.037\) | \(-0.518{\pm}0.042\) | \(-0.468{\pm}0.045\) | \(\boldsymbol{-}0.443{\pm}0.044\) |
| 21 | statlog-australian-credit | (690, 15) | \(\boldsymbol{-}0.627{\pm}0.022\) | \(\boldsymbol{-}0.636{\pm}0.030\) | \(\boldsymbol{-}0.627{\pm}0.023\) | \(\boldsymbol{-}0.627{\pm}0.023\) |
| 22 | credit-approval | (690, 16) | \(\boldsymbol{-}0.342{\pm}0.008\) | \(\boldsymbol{-}0.343{\pm}0.012\) | \(\boldsymbol{-}0.341{\pm}0.008\) | \(\boldsymbol{-}0.341{\pm}0.009\) |
| 23 | breast-cancer-wisc | (699, 10) | \(\boldsymbol{-}0.091{\pm}0.030\) | \(\boldsymbol{-}0.092{\pm}0.028\) | \(\boldsymbol{-}0.091{\pm}0.037\) | \(\boldsymbol{-}0.091{\pm}0.037\) |
| 24 | blood | (748, 5) | \(\boldsymbol{-}0.475{\pm}0.043\) | \(\boldsymbol{-}0.476{\pm}0.045\) | \(\boldsymbol{-}0.476{\pm}0.044\) | \(\boldsymbol{-}0.476{\pm}0.044\) |
| 25 | pima | (768, 9) | \(\boldsymbol{-}0.470{\pm}0.031\) | \(\boldsymbol{-}0.472{\pm}0.035\) | \(\boldsymbol{-}0.471{\pm}0.033\) | \(\boldsymbol{-}0.471{\pm}0.033\) |
| 26 | mammographic | (961, 6) | \(\boldsymbol{-}0.408{\pm}0.037\) | \(\boldsymbol{-}0.408{\pm}0.041\) | \(\boldsymbol{-}0.408{\pm}0.039\) | \(\boldsymbol{-}0.408{\pm}0.039\) |
| 27 | statlog-german-credit | (1000, 25) | \(\boldsymbol{-}0.493{\pm}0.040\) | \(\boldsymbol{-}0.493{\pm}0.041\) | \(\boldsymbol{-}0.493{\pm}0.043\) | \(\boldsymbol{-}0.494{\pm}0.043\) |
| Bold Count | \(20\) | \(20\) | \(22\) | \(27\) |
10pt
| (\(n\), \(d\)) | LA | EP | VI | Ours | ||
|---|---|---|---|---|---|---|
| trains | (10, 30) | \(\boldsymbol{0}.700{\pm}0.400\) | \(\boldsymbol{0}.800{\pm}0.245\) | \(\boldsymbol{0}.800{\pm}0.245\) | \(\boldsymbol{0}.800{\pm}0.245\) | |
| balloons | (16, 5) | \(\boldsymbol{0}.667{\pm}0.298\) | \(\boldsymbol{0}.667{\pm}0.298\) | \(\boldsymbol{0}.667{\pm}0.298\) | \(\boldsymbol{0}.667{\pm}0.298\) | |
| fertility | (100, 10) | \(\boldsymbol{0}.880{\pm}0.060\) | \(\boldsymbol{0}.880{\pm}0.060\) | \(\boldsymbol{0}.880{\pm}0.060\) | \(\boldsymbol{0}.880{\pm}0.060\) | |
| pittsburg-bridges-T-OR-D | (102, 8) | \(\boldsymbol{0}.863{\pm}0.036\) | \(\boldsymbol{0}.883{\pm}0.066\) | \(\boldsymbol{0}.863{\pm}0.036\) | \(\boldsymbol{0}.863{\pm}0.036\) | |
| acute-nephritis | (120, 7) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | |
| acute-inflammation | (120, 7) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | \(\boldsymbol{1}.000{\pm}0.000\) | |
| echocardiogram | (131, 11) | \(0.808{\pm}0.061\) | \(\boldsymbol{0}.847{\pm}0.043\) | \(\boldsymbol{0}.785{\pm}0.076\) | \(0.778{\pm}0.063\) | |
| hepatitis | (155, 20) | \(\boldsymbol{0}.813{\pm}0.024\) | \(\boldsymbol{0}.813{\pm}0.032\) | \(\boldsymbol{0}.813{\pm}0.024\) | \(\boldsymbol{0}.832{\pm}0.024\) | |
| parkinsons | (195, 23) | \(\boldsymbol{0}.959{\pm}0.048\) | \(0.892{\pm}0.075\) | \(\boldsymbol{0}.944{\pm}0.050\) | \(\boldsymbol{0}.959{\pm}0.048\) | |
| breast-cancer-wisc-prog | (198, 34) | \(\boldsymbol{0}.793{\pm}0.051\) | \(\boldsymbol{0}.793{\pm}0.069\) | \(\boldsymbol{0}.793{\pm}0.051\) | \(\boldsymbol{0}.793{\pm}0.051\) | |
| spect | (265, 23) | \(\boldsymbol{0}.706{\pm}0.031\) | \(\boldsymbol{0}.698{\pm}0.027\) | \(\boldsymbol{0}.702{\pm}0.028\) | \(\boldsymbol{0}.706{\pm}0.023\) | |
| statlog-heart | (270, 14) | \(\boldsymbol{0}.830{\pm}0.036\) | \(\boldsymbol{0}.833{\pm}0.039\) | \(\boldsymbol{0}.830{\pm}0.036\) | \(\boldsymbol{0}.826{\pm}0.034\) | |
| haberman-survival | (306, 4) | \(\boldsymbol{0}.725{\pm}0.039\) | \(\boldsymbol{0}.719{\pm}0.036\) | \(\boldsymbol{0}.725{\pm}0.039\) | \(\boldsymbol{0}.725{\pm}0.039\) | |
| ionosphere | (351, 34) | \(\boldsymbol{0}.932{\pm}0.025\) | \(\boldsymbol{0}.932{\pm}0.024\) | \(\boldsymbol{0}.946{\pm}0.024\) | \(\boldsymbol{0}.946{\pm}0.028\) | |
| horse-colic | (368, 26) | \(\boldsymbol{0}.799{\pm}0.035\) | \(\boldsymbol{0}.807{\pm}0.032\) | \(\boldsymbol{0}.791{\pm}0.045\) | \(\boldsymbol{0}.802{\pm}0.039\) | |
| congressional-voting | (435, 17) | \(\boldsymbol{0}.605{\pm}0.024\) | \(\boldsymbol{0}.593{\pm}0.014\) | \(\boldsymbol{0}.595{\pm}0.013\) | \(\boldsymbol{0}.591{\pm}0.016\) | |
| cylinder-bands | (512, 36) | \(0.785{\pm}0.037\) | \(\boldsymbol{0}.777{\pm}0.044\) | \(\boldsymbol{0}.791{\pm}0.034\) | \(\boldsymbol{0}.803{\pm}0.031\) | |
| breast-cancer-wisc-diag | (569, 31) | \(\boldsymbol{0}.972{\pm}0.010\) | \(\boldsymbol{0}.974{\pm}0.019\) | \(\boldsymbol{0}.977{\pm}0.012\) | \(\boldsymbol{0}.977{\pm}0.011\) | |
| ilpd-indian-liver | (583, 10) | \(\boldsymbol{0}.719{\pm}0.025\) | \(\boldsymbol{0}.712{\pm}0.020\) | \(\boldsymbol{0}.717{\pm}0.029\) | \(\boldsymbol{0}.719{\pm}0.028\) | |
| monks-2 | (601, 7) | \(\boldsymbol{0}.740{\pm}0.049\) | \(0.719{\pm}0.039\) | \(\boldsymbol{0}.744{\pm}0.046\) | \(\boldsymbol{0}.762{\pm}0.045\) | |
| statlog-australian-credit | (690, 15) | \(\boldsymbol{0}.678{\pm}0.028\) | \(\boldsymbol{0}.677{\pm}0.021\) | \(\boldsymbol{0}.678{\pm}0.028\) | \(\boldsymbol{0}.678{\pm}0.028\) | |
| credit-approval | (690, 16) | \(\boldsymbol{0}.859{\pm}0.026\) | \(\boldsymbol{0}.864{\pm}0.020\) | \(\boldsymbol{0}.864{\pm}0.024\) | \(\boldsymbol{0}.862{\pm}0.026\) | |
| breast-cancer-wisc | (699, 10) | \(\boldsymbol{0}.969{\pm}0.016\) | \(\boldsymbol{0}.969{\pm}0.016\) | \(\boldsymbol{0}.969{\pm}0.016\) | \(\boldsymbol{0}.969{\pm}0.016\) | |
| blood | (748, 5) | \(\boldsymbol{0}.785{\pm}0.042\) | \(\boldsymbol{0}.785{\pm}0.041\) | \(\boldsymbol{0}.786{\pm}0.044\) | \(\boldsymbol{0}.786{\pm}0.044\) | |
| pima | (768, 9) | \(\boldsymbol{0}.764{\pm}0.027\) | \(\boldsymbol{0}.766{\pm}0.025\) | \(\boldsymbol{0}.767{\pm}0.026\) | \(\boldsymbol{0}.767{\pm}0.026\) | |
| mammographic | (961, 6) | \(\boldsymbol{0}.824{\pm}0.019\) | \(\boldsymbol{0}.823{\pm}0.017\) | \(\boldsymbol{0}.823{\pm}0.019\) | \(\boldsymbol{0}.823{\pm}0.019\) | |
| statlog-german-credit | (1000, 25) | \(\boldsymbol{0}.770{\pm}0.039\) | \(\boldsymbol{0}.763{\pm}0.038\) | \(\boldsymbol{0}.768{\pm}0.038\) | \(\boldsymbol{0}.769{\pm}0.037\) | |
| Bold Count | \(25\) | \(25\) | \(27\) | \(26\) |
Convergence of VI To ensure that the comparison to VI is as fair as possible, we ran both the vanilla VI approach where we jointly optimize \(\boldsymbol{\xi}\) and \(\boldsymbol{\theta}\) using L-BFGS-B and the CVI approach by [13] that uses natural gradients for the E-step for faster convergence. The speed of convergence was not the main interest, and thus we verified that the VI results obtained by the two different approaches gave the same results—thus confirming that the VI results presented in the tables are all for converged optimization runs.
11 Robust (Student-\(t\)) Regression↩︎
For additional insight, we include results for a Student-\(t\) likelihood model that allows heavy-tailed noise in the observations. This likelihood is not log-concave, which makes LA and EP more challenging. Previous works in the field do not list many standard data sets for benchmarking, but we have gathered three previously used benchmark problems for comparison.
11.1 Experiment Setup↩︎
We preprocessed the data and selected an interval of 1000 data points from the original data. We initialize all methods with unit lengthscale, kernel magnitude, and likelihood variance. We fix the degrees of freedom in the likelihood to \(\nu=3\). For LA and EP, we follow the methods designed in [15]. For VI and our hybrid training procedure, E and M steps each have 20 iterations. In the E-step we set the learning rate of natural gradient descent to be \(0.001\). In the M-step we use the Adam optimizer [19] and set the learning rate to \(0.001\). For neal we set the maximal steps to be \(2000\) and for boston and stock we set the maximal steps to be \(5000\).
6pt
| Data set | titanic | bank | twonorm | mushroom | magic |
|---|---|---|---|---|---|
| (\(n\), \(d\)) | (2201, 4) | (4521, 17) | (7400, 21) | (8124, 22) | (19020, 11) |
12 Evaluation on Sparse Approximation↩︎
To further study the proposed approach, we include results for a couple of sparse GP classification problems as proof-of-concept.
12.1 Experiment Setup↩︎
We initialize all methods with unit lengthscale and magnitude. We use \(k\)-means to select a set of \(500\) inducing points and then fix the location of inducing points. Learning the inducing points would add an additional layer of optimization, and this is not in the scope of this paper. We use 20 iterations for both the E and M steps. In the E-step we set the learning rate of natural gradient descent to \(0.1\). In the M-step we use the Adam optimizer [19] and set the learning rate to \(0.01\). The data sets information are given in 11.
References↩︎
In practice it may be beneficial to optimize in the whitened (or non-centered) parameterization \(\boldsymbol{\xi}= (\mathbf{m}', \mathbf{S}')\) s.t. \(\mathbf{m}= \mathbf{L}\mathbf{m}'\) and \(\mathbf{S}= \mathbf{L}\mathbf{S}' \mathbf{L}^\top\), where \(\mathbf{L}= \operatorname{Cholesky}(\mathbf{K})\) [18].↩︎