Parametric Dependence of Bound States in the Continuum on Periodic Structures
January 01, 1970
Abstract
Bound states in the continuum (BICs) have some unusual properties and important applications in photonics. A periodic structure sandwiched between two homogeneous media is the most popular platform for observing BICs and realizing their applications. Existing studies on BICs assume the periodic structure has a \(C_2\) rotational symmetry about the axis perpendicular to the periodic layer. It is known that all BICs turn to resonant states with finite quality factors if the periodic structure is perturbed by a generic perturbation breaking the \(C_2\) symmetry, and a typical BIC continues to exist if the perturbation keeps the \(C_2\) symmetry. We study how typical BICs depend on generic structural parameters. For a class of BICs with one opening radiation channel, we show that in the plane of two generic parameters, the BICs exist continuously as a curve. Consequently, BICs can exist on periodic structures without the \(C_2\) symmetry, and they can be found by tuning a single structural parameter. The result is established analytically by a perturbation theory with two independent perturbations and validated by numerical examples. Our study reveals a much larger family for BICs on periodic structures, and provides new opportunities for future applications.
A bound state in the continuum (BIC) is a localized eigenmode that does not couple with compatible waves propagating to or from infinity [1]–[3]. For photonic systems, BICs can exist in various structures including waveguides with local distortions [4], waveguides with lateral leaky channels [5]–[7], layered anisotropic media [8], rotationally symmetric periodic structures [9], [10], and periodic structures sandwiched between two homogeneous media [11]–[22]. Since a BIC can be regarded as a resonant state with an infinite quality factor (\(Q\) factor), it is possible to realize resonant states with extremely large \(Q\) factors by perturbing the structures [23]–[26] or varying the Bloch wavevector [27], [28]. Although true BICs can only exist on structures that are unbounded in at least one spatial direction, they have inspired the design of wavelength-scale structures supporting high-\(Q\) resonances [29], [30]. Due to their unusual properties, the BICs are useful in a number of applications such as lasing [31], sensing [32], [33], filtering and switching, and can be used to enhance various emmisive processes and nonlinear optical effects [34]–[36].
On a periodic structure (with one or two periodic directions) sandwiched between two homogeneous media, a BIC is either a standing wave or a propagating Bloch mode. In all existing studies [11]–[21], the periodic structure is assumed to have at least the \(180^\circ\) (i.e. \(C_2\)) rotational symmetry about the axis \(z\) perpendicular to the periodic layer. Some standing waves are symmetry-protected BICs. Their existence can be rigorously proved, and they are robust against small structural perturbations that preserve the \(C_2\) symmetry. Most propagating BICs are found on periodic structures with not only the \(C_2\) symmetry but also a reflection symmetry in \(z\) [11], [13]–[15], [17]–[21]. The existence and robustness of the propagating BICs (as well as the standing waves) have been studied using topological properties [9], [15], [18]. It has been proved that a generic propagating BIC on a periodic structure with both the \(C_2\) symmetry and the reflection symmetry in \(z\) is robust against small structural perturbations that preserve these two symmetries [15], [18], [37], [38]. It is also known that a BIC always turns to a resonant state with a finite \(Q\) factor, if the periodic structure is perturbed by a generic perturbation breaking the \(C_2\) symmetry [23]–[25].
In this Letter, we study how BICs depend on generic structural parameters. More precisely, in a generic parameter space, what is the dimension of the object formed by the BIC parameter values? It is clear that the answer depends on the number of opening radiation channels. For the simplest case of one opening radiation channel, we show that in the plane of two generic parameters, the BICs exist as a curve, and in general, the BICs form a codimension-1 object in parameter space. This implies that on a periodic structure without the \(C_2\) symmetry, it is possible to find BICs by tuning one structural parameter. We establish this result using a perturbation theory with two parameters. Assuming a periodic structure has a BIC with a frequency in the range for one opening radiation channel, we consider a perturbed structure with two independent perturbations where the amplitude of the first perturbation is fixed, and show that if the amplitude of the second perturbation is properly chosen, then the perturbed structure also has a BIC. The result requires some generic conditions on the original BIC of the unperturbed structure and the perturbation profiles.
To simplify the presentation, we consider a two-dimensional (2D) dielectric structure that is invariant in \(x\), periodic in \(y\), and symmetric in \(z\). The dielectric function \(\varepsilon({\boldsymbol{r}})\) for \({\boldsymbol{r}} = (y,z)\), satisfies \[\label{refper} \varepsilon({\boldsymbol{r}}) = \varepsilon(y,-z)=\varepsilon(y+L, z)\tag{1}\] for all \({\boldsymbol{r}}\), where \(L\) is the period. In addition, it is assumed that the thickness of the periodic layer is \(2d\) and the surrounding medium is vacuum. Therefore, \(\varepsilon({\boldsymbol{r}}) = 1\) for \(|z| > d\). Notice that we do not assume a reflection symmetry in \(y\) which is equivalent to the \(C_2\) rotational symmetry for the 2D structure. For the \(E\) polarization, the \(x\) component of the electric field, denoted as \(u\), satisfies the following Helmholtz equation \[\label{helm} \partial_y^2 u + \partial_z^2 u + k^2 \varepsilon({\boldsymbol{r}}) u = 0,\tag{2}\] where \(k=\omega/c\) is the freespace wavenumber, \(\omega\) is the angular frequency and \(c\) is the speed of light in vacuum. A BIC is a Bloch mode solution of Eq. (2 ) given as \(u({\boldsymbol{r}}) = \phi({\boldsymbol{r}}) e^{ i \beta y}\), where \(\phi\) is periodic in \(y\) with period \(L\) and decays to zero as \(|z| \to \infty\), and \(\beta\) is a real Bloch wavenumber satisfying \(|\beta | \le \pi/L\) and \(|\beta| < k\).
First, we assume that a particular periodic structure with a dielectric function \(\varepsilon_*({\boldsymbol{r}})\) satisfying the conditions above has a non-degenerate BIC \(u_* ({\boldsymbol{r}}) = \phi_*({\boldsymbol{r}}) e^{ i \beta_* y}\) with a frequency \(\omega_*\) satisfying \[\label{1channel} |\beta_* | < k_* = \frac{\omega_*}{c} < \frac{2\pi}{L} - |\beta_*|.\tag{3}\] The above inequalities ensure that there is only one opening radiation channel. Due to the reflection symmetry in \(z\), the BIC \(u_*\) is either even in \(z\) or odd in \(z\).
For the same \(k_*\) and \(\beta_*\), we have diffraction problems for incident plane waves \(\exp[ i (\beta_* y \pm \alpha_* z) ]\) where \(\alpha_* = \sqrt{k_*^2 - \beta_*^2} > 0\), given in the media below and above the periodic layer. If the BIC is even in \(z\), we can construct a diffraction solution that is also even in \(z\). We write the diffraction solution as \(v({\boldsymbol{r}})= \psi({\boldsymbol{r}}) \exp (i \beta_* y)\), where \(\psi\) is periodic in \(y\) with period \(L\), and require \(v({\boldsymbol{r}})\) and the BIC be orthogonal, i.e., \[\label{ortho} \int_\Omega \varepsilon_*({\boldsymbol{r}}) \, \overline{v} \, u_* \, d{\boldsymbol{r}} = \int_\Omega \varepsilon_*({\boldsymbol{r}}) \, \overline{\psi} \, \phi_* \, d{\boldsymbol{r}} = 0,\tag{4}\] where \(\Omega\) is the domain for one period of the structure given by \(|y| < L/2\) and \(|z| < \infty\), \(\overline{v}\) is the complex conjugate of \(v\), etc. This is possible, because the diffraction solution is not unique. If \(v({\boldsymbol{r}})\) is a diffraction solution, so is \(v({\boldsymbol{r}}) + C u_*({\boldsymbol{r}})\) for any constant \(C\). It is always possible to choose \(C\) to redefine \(v\), such that Eq. (4 ) is satisfied. Similarly, if the BIC is odd in \(z\), there is an odd-in-\(z\) diffraction solution \(v({\boldsymbol{r}})\) satisfying the orthogonality condition (4 ). To analyze the parametric dependence of BICs, we need the following condition \[\label{a21} \int_\Omega \overline{v} \frac{\partial u_*}{\partial y} d{\boldsymbol{r}} = \int_\Omega \overline{\psi} \left( i \beta_* \phi_* + \frac{ \partial \phi_*}{\partial y} \right) \, d{\boldsymbol{r}} \ne 0.\tag{5}\] If the above is valid, we scale the diffraction solution or the BIC, such that \[\label{a21p} \int_\Omega \overline{\psi} \left( \beta_* \phi_* - i \frac{\partial \phi_*}{\partial y} \right) d{\boldsymbol{r}} > 0.\tag{6}\]
If the periodic structure depends on parameters, the dielectric function may be written as \(\varepsilon = \varepsilon({\boldsymbol{r}}, {\boldsymbol{p}})\), where \({\boldsymbol{p}}\) is a vector of real parameters. Assuming a BIC exists for a particular parameter value \({\boldsymbol{p}}_*\), we study the existence of BICs for \({\boldsymbol{p}}\) near \({\boldsymbol{p}}_*\). Since \(\varepsilon({\boldsymbol{r}}, {\boldsymbol{p}})\) can be approximated by \(\varepsilon({\boldsymbol{r}}, {\boldsymbol{p}}_* ) + \nabla_{\boldsymbol{p}} \varepsilon({\boldsymbol{r}}, {\boldsymbol{p}}_*) \cdot ({\boldsymbol{p}} -{\boldsymbol{p}}_*)\), we consider, for the case of two parameters, a perturbed periodic structure with a dielectric function given by \[\label{peps} \varepsilon({\boldsymbol{r}}) = \varepsilon_* ({\boldsymbol{r}}) + \delta G({\boldsymbol{r}}) + \gamma F({\boldsymbol{r}}),\tag{7}\] where \(\delta\) and \(\gamma\) are components of \({\boldsymbol{p}} - {\boldsymbol{p}}_*\), \(F\) and \(G\) (the perturbation profiles) are partial derivatives of \(\varepsilon({\boldsymbol{r}}, {\boldsymbol{p}})\) with respect to the components of \({\boldsymbol{p}}\). We assume both \(F\) and \(G\) are \(O(1)\) real functions, are periodic in \(y\) with period \(L\) and symmetric in \(z\), and vanish when \(|z| > d\). Thus, the perturbations preserve the periodicity in \(y\) and the reflection symmetry in \(z\) and do not affect the surrounding homogeneous media. In addition, we assume the perturbation profile \(F\) satisfies \[\label{condF} Im \int_\Omega \overline{\psi}({\boldsymbol{r}}) F({\boldsymbol{r}}) \phi_* ({\boldsymbol{r}}) \, d{\boldsymbol{r}} \ne 0,\tag{8}\] where \(\phi_*\) and \(\psi\) have their relative phase fixed by condition (6 ).
Our main result can be stated as follows: If the periodic structure with the dielectric function \(\varepsilon_* ({\boldsymbol{r}})\) has a non-degenerate BIC \(\{ \phi_*, k_*, \beta_* \}\) and an associated diffraction solution \(\psi({\boldsymbol{r}})\) satisfying conditions (3 ) and (6 ), and the perturbation profile \(F({\boldsymbol{r}})\) satisfies condition (8 ), then for any real \(\delta\) near \(0\), there is a real \(\gamma\) near 0, such that the perturbed periodic structure with \(\varepsilon({\boldsymbol{r}})\) given in Eq. (7 ) has a BIC \(\{ \phi, k, \beta \}\) with \(\phi\) close to \(\phi_*\), \(k\) close to \(k_*\) and \(\beta\) close to \(\beta_*\).
The above proposition implies that the BICs exist continuously as a curve in the plane of two generic parameters. It is clear that if there are \(m\) generic parameters, the BICs should form a codimension-1 object, i.e., an object with dimension \(m-1\), in the \(m\)-dimensional parameter space. To prove the above result, we expand the desired BIC and the parameter \(\gamma\) as power series of \(\delta\): \[\begin{align} \tag{9} \phi &=& \phi_* + \phi_1 \delta + \phi_2 \delta^2 + \cdots \\ \tag{10} \beta &=& \beta_* + \beta_1 \delta + \beta_2 \delta^2 + \cdots\\ \tag{11} k &=& k_* + k_1 \delta + k_2 \delta^2 + \cdots\\ \tag{12} \gamma &=& \gamma_1 \delta + \gamma_2 \delta^2 + \cdots \end{align}\] and show that for each \(j \ge 1\), \(\beta_j\), \(k_j\) and \(\gamma_j\) can be solved and they are real, \(\phi_j\) can be solved and it decays to 0 as \(|z| \to \infty\). Briefly, we obtain an inhomogeneous Helmholtz equation for \(\phi_j\) (see Supplemental Material [39]) and the following linear system for \(\beta_j\), \(k_j\) and \(\gamma_j\): \[\label{3by3} \left[ \begin{matrix} a_{11} & a_{12} & a_{13} \cr a_{21} & 0 & Re(a_{23}) \cr 0 & 0 & Im(a_{23}) \end{matrix} \right] \left[ \begin{matrix} \beta_j\cr k_j\cr \gamma_j \end{matrix} \right] = \left[ \begin{matrix} b_{1j} \cr Re(b_{2j}) \cr Im(b_{2j}) \end{matrix} \right],\tag{13}\] where \[\begin{align} a_{11} &=& 2 \int_\Omega \overline{\phi}_* \left( \beta_* \phi_* -i \frac{ \partial \phi_*}{\partial y} \right) d{\boldsymbol{r}} \\ a_{12} &=& -2 k_* \int_\Omega \varepsilon_* |\phi_*|^2 \, d{\boldsymbol{r}} \\ a_{13} &=& -k_*^2 \int_\Omega F({\boldsymbol{r}}) |\phi_*|^2 \, d{\boldsymbol{r}}\\ a_{21} &=& 2 \int_\Omega\overline{\psi} \left( \beta_* \phi_* -i \frac{ \partial \phi_*}{\partial y} \right) d{\boldsymbol{r}} \\ a_{23} &=& -k_*^2 \int_\Omega F({\boldsymbol{r}}) \overline{\psi} \phi_* \, d{\boldsymbol{r}}, \end{align}\] \(b_{1j}\) and \(b_{2j}\) can also be explicitly written down (see Supplemental Material [39]). Using integration by parts, it is easy to show that \(a_{11}\) is real. From condition (6 ), we see that \(a_{21}\) is also real. Therefore, all entries in the \(3 \times 3\) coefficient matrix of Eq. (13 ) are real. The second column the coefficient matrix is related to \[a_{22} = -2 k_* \int_\Omega \varepsilon_* \overline{\psi} \phi_* \, d{\boldsymbol{r}},\] and it is zero by the orthogonality assumption (4 ). Since \(a_{12}\), \(a_{21}\) and \(Im(a_{23})\) [by condition (8 )], are all nonzero, the coefficient matrix is invertible. Moreover, we can prove that \(b_{1j}\) is real for all \(j\ge 1\) (see Supplementary Material [39]), therefore, for each \(j\ge 1\), \(\beta_j\), \(k_j\) and \(\gamma_j\) can be solved and they are real. Meanwhile, we can show that the governing equation for \(\phi_j\) has a solution with the same parity (even or odd in \(z\)) as \(\phi_*\), and it decays to zero as \(|z| \to \infty\) (see Supplemental Material [39]).
Notice that \(G({\boldsymbol{r}})\) has no additional condition besides those specified below Eq. (7 ). If \(G({\boldsymbol{r}}) \equiv 0\), the above procedure does not give a new BIC, namely, we only get \(\gamma=0\) and \(u = u_*\). The same is true if \(F({\boldsymbol{r}})\) and \(G({\boldsymbol{r}})\) are proportional to each other. For example, if \(F({\boldsymbol{r}}) = G({\boldsymbol{r}})\), then \(\gamma = - \delta\) and \(u = u_*\).
If the original BIC is a standing wave (\(\beta_* =0\)), then the BIC on the perturbed structure is also a standing wave. Since \(\beta_* =0\), and the real and imaginary parts of a standing wave \(u_*\) are also standing waves. Therefore, we can assume \(u_* ({\boldsymbol{r}})=\phi_* ({\boldsymbol{r}})\) is a real function. The diffraction solution \(v({\boldsymbol{r}})\) contains normally incident and reflected plane waves below and above the periodic layer, and it can be scaled to be a pure imaginary function. Thus, \(a_{23}\) is pure imaginary. In addition, we can show that for each \(j \ge 1\), \(b_{2j}\) is pure imaginary (see Supplemental Material [39]). Therefore, the second equation in (13 ) is \(a_{21} \beta_j = 0\) and it gives \(\beta_j = 0\) for all \(j \ge 1\). This result relies on the non-degeneracy of the standing wave and is consistent with the reciprocity principle. If the perturbed structure has a BIC with Bloch wavenumber \(\beta \ne 0\), it must have another one with Bloch wavenumber \(-\beta\), and both of them are perturbations of the original standing wave \(u_*\). However, the power series (9 )-(12 ) give only one solution. This implies that the BIC on the perturbed structure must also be a standing wave.
If the original periodic structure has an additional reflection symmetry in \(y\) and \(G({\boldsymbol{r}})\) is also symmetric in \(y\), then according to our previous work [37], a perturbed structure with a dielectric function \(\varepsilon_* ({\boldsymbol{r}}) + \delta G({\boldsymbol{r}})\) should have a BIC near the original one on the unperturbed structure. Our theory developed above covers this result as a special case. If \(F({\boldsymbol{r}})\) is not symmetric in \(y\), we can show that \(\gamma_j = 0\) for all \(j \ge 1\) (see Supplemental Material [39]). Therefore, a BIC exists on the perturbed structure with only one perturbation \(\delta G({\boldsymbol{r}})\). If \(F({\boldsymbol{r}})\) is also symmetric in \(y\), then condition (8 ) is not satisfied, thus, \(\gamma\) cannot be determined as a function of \(\delta\). In fact, for any small \(\gamma\), \(\delta G({\boldsymbol{r}}) + \gamma F({\boldsymbol{r}})\) is a perturbation preserving the reflection symmetry in \(y\), and there should be a BIC on the perturbed structure.
To validate the above theory, we consider a periodic array of circular cylinders surrounded by vacuum as shown in Fig. 1.
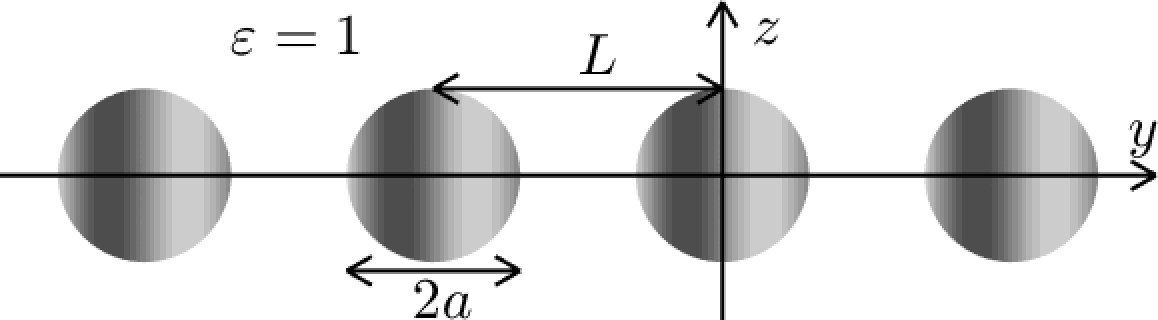
Figure 1: A periodic array of circular cylinders with radius \(a\) and a \(y\)-dependent dielectric function. The array is symmetric in \(z\) and asymmetric in \(y\).
The radius of the cylinders is \(a=0.3L\), where \(L\) is the period in the \(y\) direction. The dielectric function \(\varepsilon({\boldsymbol{r})}\) of the structure is given by Eq. (7 ) with \(\varepsilon_*({\boldsymbol{r}}) = 10\), \[F({\boldsymbol{r}}) = \sin \left( \dfrac{\pi y}{2 a} + \dfrac{\pi}{4}\right), \; G({\boldsymbol{r}}) = \sin \left( \dfrac{\pi y}{a}\right),\] if \({\boldsymbol{r}}\) is inside the cylinders, i.e., for an integer \(m\), \(y\) and \(z\) satisfy \((y-m L)^2 + z^2 < a^2\), and \(\varepsilon_* ({\boldsymbol{r}}) = 1\) and \(F({\boldsymbol{r}}) = G({\boldsymbol{r}}) = 0\) if \({\boldsymbol{r}}\) is outside the cylinders. For nonzero \(\delta\) and \(\gamma\), the periodic array is symmetric in \(z\) and asymmetric in \(y\). For \(\delta=\gamma=0\), the periodic array is symmetric in \(y\), and has a standing wave with freespace wavenumber \(k_* = 0.4414 (2\pi/L)\) and a propagating BIC with \(k_* =0.6173 (2\pi/L)\) and Bloch wavenumber \(\beta_* = 0.2206 (2\pi/L)\). The standing wave is anti-symmetric in \(y\), i.e., it is a symmetry-protected BIC.
For a proper \(\gamma\) depending on \(\delta\), the BICs exist continuously with respect to \(\delta\). Using an efficient numerical method, we calculated the BICs for \(0 \le \delta \le 1\). As predicted by our theory, the standing wave for \(\delta=\gamma=0\) continues as a standing wave for \(\delta \ne 0\). In Figs. 2 (a) and 2 (b),
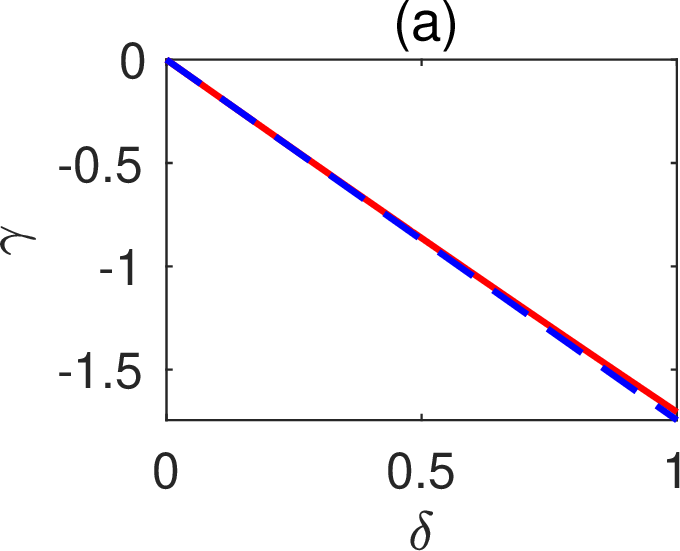
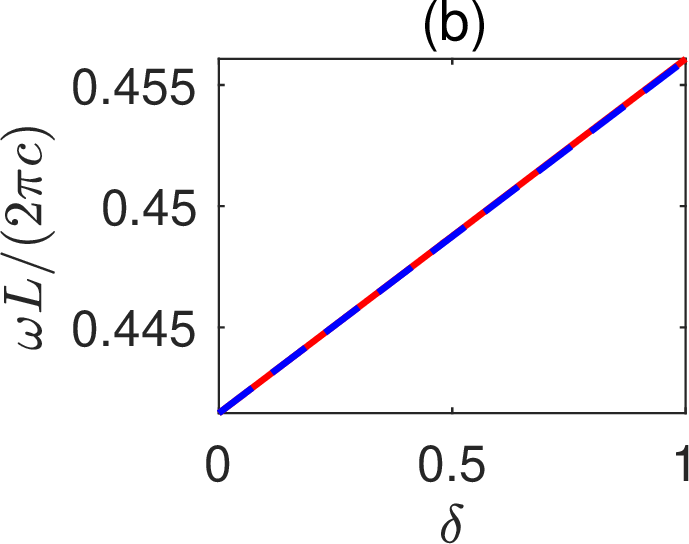
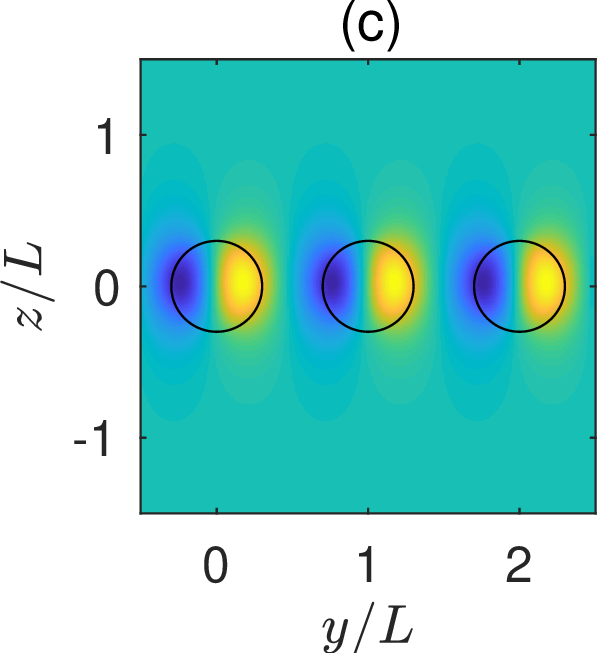
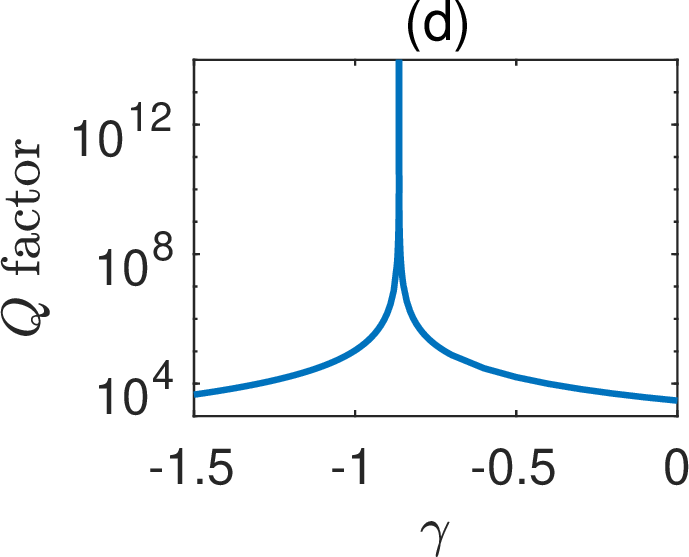
Figure 2: Standing wave on a periodic array without a reflection symmetry in \(y\): (a) \(\gamma\) as a function of \(\delta\) for the existence of the standing wave; (b) frequency of the standing wave as a function of \(\delta\); (c) wave field pattern of the standing wave for \(\delta = 0.5\) and \(\gamma = -0.863673\); (d) \(Q\) factors of the resonant states for \(\beta=0\), \(\delta=0.5\) and different values of \(\gamma\)..
the solid red curves depict \(\gamma\) and freespace wavenumber \(k\) as functions of \(\delta\) for the standing wave. Based on the standing wave for \(\delta=\gamma=0\), we found the first order perturbation terms \(k_1 = 0.0146 (2\pi/L)\) and \(\gamma_1=-1.7491\). The first order perturbation results, i.e. \(\gamma \approx \gamma_1 \delta\) and \(k \approx k_* + k_1 \delta\) are shown in Figs. 2 (a) and 2 (b) as the blue dashed lines, and they are quite accurate even when \(\delta\) is not small. For \(\delta=0.5\), the standing wave is obtained at \(\gamma = -0.863673\) and it is shown in Fig. 2 (c). For other values of \(\gamma\), the periodic structure can only have resonant states with complex frequencies. In Fig. 2 (d), we show the \(Q\) factors of the resonant states as a function of \(\gamma\) for \(\delta = 0.5\) and \(\beta = 0\), where the infinite peak corresponds to the standing wave.
The propagating BIC for \(\delta=\gamma=0\) can also be easily extended to the case with \(\delta \ne 0\). In Figs. 3 (a), 3 (b) and 3 (c),
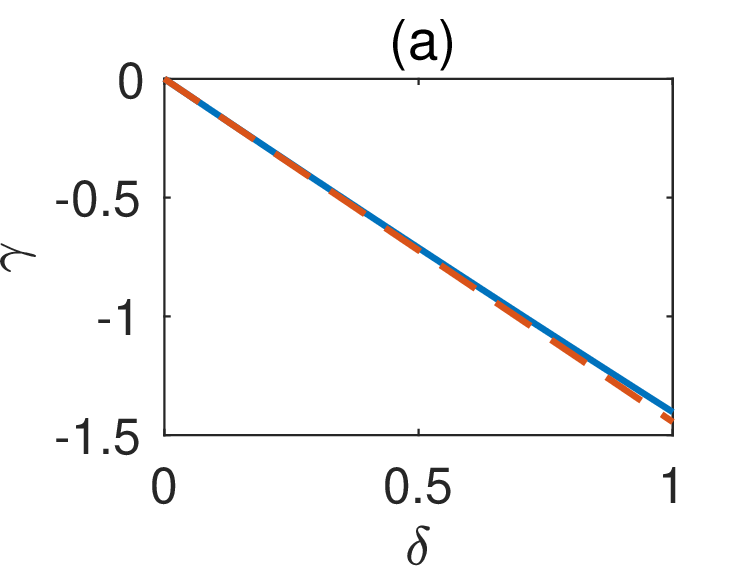
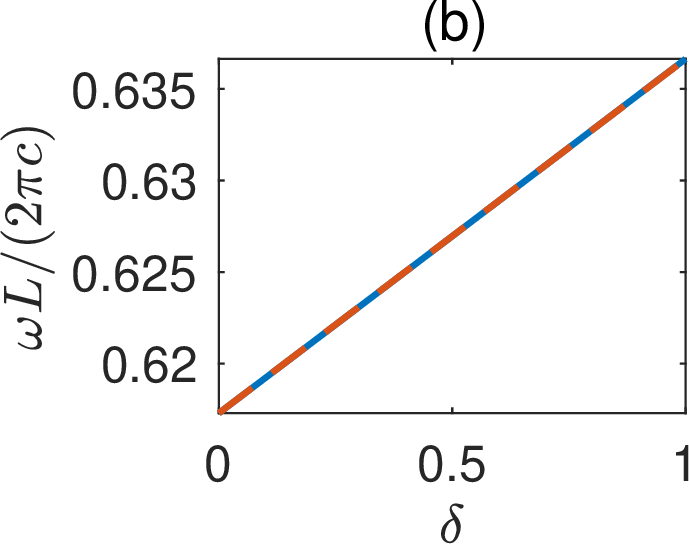
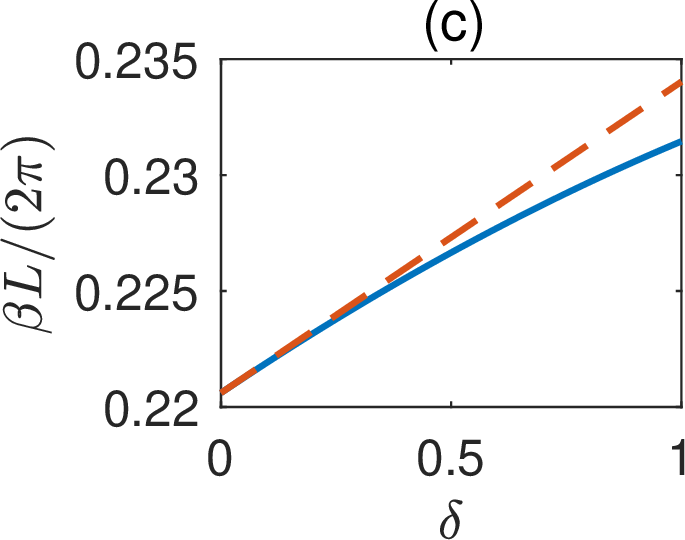
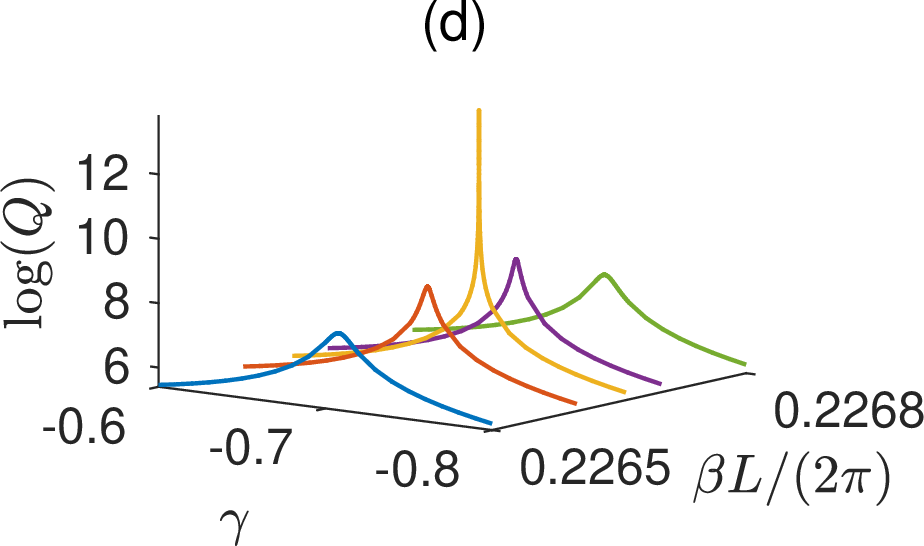
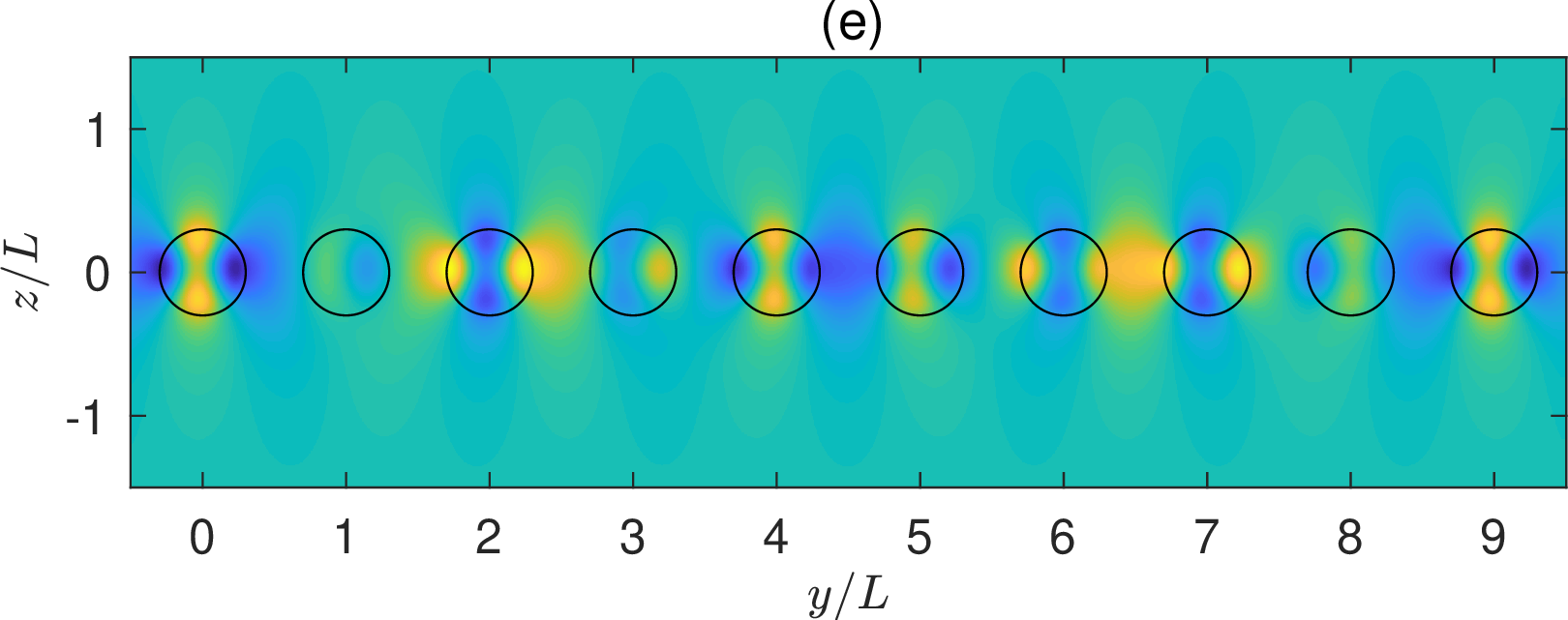
Figure 3: Propagating BIC on a periodic array without a reflection symmetry in \(y\): (a) \(\gamma\) as a function of \(\delta\) for the existence of the BIC; (b) frequency of the propagating BIC; (c) Bloch wavenumber of the propagating BIC; (d) \(Q\) factors of the resonant states for \(\delta=0.5\) and different values of \(\beta\) and \(\gamma\); (e) wave field pattern, i.e., \(Re[u({\boldsymbol{r}})]\), of the propagating BIC for \(\delta = 0.5\) and \(\gamma = -0.711932\)..
we show \(\gamma\), \(k\) and \(\beta\) as functions of \(\delta\) for the propagating BIC, respectively. The first order perturbation terms are found as \(\gamma_1 = -1.4445\), \(k_1 = 0.0193 (2\pi/L)\), and \(\beta_1 = 0.0134 (2\pi/L)\). In Figs. 3 (a), 3 (b) and 3 (c), the first order perturbation results are shown as the red dashed lines. For \(\delta = 0.5\) and \(\gamma = -0.711932\), the periodic structure supports a propagating BIC with \(k = 0.626957 (2\pi/L)\) and \(\beta = 0.226658 (2\pi/L)\). Its field pattern is shown in Fig. 3 (e). As shown in Fig. 3 (d), the periodic structure has resonant states with finite \(Q\) factors for nearby values of \(\gamma\) and \(\beta\).
In summary, we show analytically that if there is only one radiation channel, typical BICs on periodic structures form codimension-1 objects in the space of generic structural parameters, and consequently, on periodic structures without the \(C_2\) rotational symmetry, it is possible to find BICs by tuning one structural parameter. The result is established by analyzing a perturbation with two independent terms. Some generic conditions are needed for the periodic structure, the perturbations and the original BIC. The reflection symmetry in \(z\) and condition (3 ) are imposed such that there is only one independent radiation channel. The BIC must be non-degenerate and must satisfy condition (5 ), and the perturbation profile \(F({\boldsymbol{r}})\) must satisfy condition (8 ). Our theory and numerical results are presented for 2D periodic structures with a single periodic direction. We are currently completing an extension for three-dimensional bi-periodic structures. It may be possible to develop similar theories for BICs on other structures, such as rotationally-symmetric periodic structures [9], [10] and waveguides with lateral leaky channels [7].
The authors acknowledge support from the Natural Science Foundation of Chongqing, China, under Grant No. cstc2019jcyj- msxmX0717, and the Research Grants Council of Hong Kong Special Administrative Region, China, under Grant No. CityU 11304117.
Supplemental material for “Bound States in the Continuum on Periodic Structures without \(C_2\) Rotational Symmetry”
1 S1: Perturbation process↩︎
On a 2D periodic structure that is invariant in \(x\), periodic in \(y\) with period \(L\), and symmetric in \(z\), a Bloch mode for the \(E\) polarization is given as \(u({\boldsymbol{r}}) = \phi({\boldsymbol{r}}) e^{ i \beta y}\) for \({\boldsymbol{r}}=(y,z)\), where \(\phi\) satisfies \[\label{eq:helm2} \frac{\partial^2 \phi}{\partial z^2} + \frac{\partial^2 \phi}{\partial y^2} + 2 i \beta \frac{\partial \phi}{\partial y} + [ k^2 \varepsilon({\boldsymbol{r}}) - \beta^2 ] \phi = 0.\tag{14}\] The dielectric function \(\varepsilon({\boldsymbol{r}})\) of the periodic structure is assumed to be \(\varepsilon({\boldsymbol{r}}) = \varepsilon_* ({\boldsymbol{r}}) + \gamma F({\boldsymbol{r}}) + \delta G({\boldsymbol{r}})\), where \(\varepsilon_*({\boldsymbol{r}})\) is the dielectric function of the original unperturbed structure, \(F\) and \(G\) are perturbation profiles, \(\delta\) and \(\gamma\) are small real parameters. We assume the unperturbed structure supports a BIC \(u_*({\boldsymbol{r}}) = \phi_*({\boldsymbol{r}}) e^{ i \beta_* y}\) with frequency \(\omega_*=k_* c\). Since the unperturbed structure also has a reflection symmetry in \(z\), we can construct a diffraction solution \(v({\boldsymbol{r}}) = \psi({\boldsymbol{r}})e^{ i \beta_* y}\) with the same even or odd parity in \(z\) as the BIC \(u_*({\boldsymbol{r}})\). The diffraction solution is not unique, we can choose \(v\) such that \[\label{dhuapoyx} \int_\Omega \varepsilon_* \overline{\psi} \phi_* d{\boldsymbol{r}} = 0,\tag{15}\] where \(\Omega\) is given by \(|y| < L/2\) and \(|z| < \infty\). Moreover, we assume \[\int_\Omega \overline{v} \frac{\partial u_*}{\partial y} d{\boldsymbol{r}} \ne 0.\] If the above is true, we scale the diffraction solution, such that \[\label{vqmtwkip} \int_\Omega \overline{\psi} \left[ \beta_* \phi_* - i \frac{\partial \phi_*}{\partial y} \right] d{\boldsymbol{r}} > 0.\tag{16}\] Finally, the perturbation profile \(F\) is required to satisfy \[\label{tigxaqeb} Im \int_\Omega F \overline{v} u_* d{\boldsymbol{r}} = Im \int_\Omega F \overline{\psi} \phi_* d{\boldsymbol{r}} \ne 0.\tag{17}\]
For a given small \(\delta\), we try to determine \(\gamma\) such that the Bloch mode \(u({\boldsymbol{r}})\) is a BIC. Expanding \(\phi\), \(\beta\), \(k\) and \(\gamma\) in power series of \(\delta\), and comparing coefficients of \(\delta^j\) for \(j \ge 1\), we obtain \[\label{phij} \mathcal{L} \phi_j = B_1 \beta_j + B_2 k_j + B_3 \gamma_j - C_j,\tag{18}\] where \[\begin{align} \mathcal{L} &=& \partial_z^2 + \partial_y^2 + 2 i \beta_* \partial_y + k_*^2 \varepsilon_* - \beta_*^2\\ B_1 &=& 2 \beta_* \phi_* - 2 i \frac{\partial \phi_*}{\partial y} \\ B_2 &=& -2 k_* \varepsilon_* \phi_* \\ B_3 &=& - k_*^2 F \phi_* \\ C_j &=& V_j \phi_* + \sum\limits_{n=1}^{j-1} W_n \phi_{j-n} + 2 i \sum\limits_{n=1}^{j-1} \beta_n \frac{ \partial \phi_{j-n}}{\partial y} \\ V_j &=& \sum\limits_{m=1}^{j-1} (k_m k_{j-m} \varepsilon_* - \beta_m \beta_{n-m}) + G \sum\limits_{m=0}^{j-1} k_m k_{j-1-m} + F \sum\limits_{m=1}^{j-1} \sum\limits_{l=0}^{m} k_l k_{m-l} \gamma_{j-m} \\ W_n &=& V_n + 2 k_* k_n \epsilon_* - 2 \beta_* \beta_n + k_*^2 \gamma_n F, \qquad 1 \leq n \leq j-1. \end{align}\] In the above, we set \(\beta_0 = \beta_*\), \(k_0 = k_*\), \(\gamma_0 = 0\), and \(\phi_0 = \phi_*\) in the sum terms. Notice that \(C_j\) only involves \(\beta_m\), \(k_m\), \(\gamma_m\) and \(\phi_m\) for \(m \leq j-1\). More specifically, \[\begin{align} && C_1 = V_1 \phi_* = k_*^2 G \phi_* \\ && C_2 = V_2 \phi_* + W_1 \phi_1 + 2 i \beta_1 \partial_y \phi_1 \\ &&= (k_1^2 \varepsilon_* - \beta_1^2 + 2 k_* k_1 G + 2 k_* k_1 \gamma_1 F) \phi_* + (2k_* k_1 \varepsilon_* - 2 \beta_* \beta_1 + k_*^2 G + k_*^2 \gamma_1 F) \phi_1 +2 i \beta_1 \partial_y \phi_1. \end{align}\]
If Eq. (18 ) has a solution \(\phi_j\) that decays to 0 as \(|z| \to \infty\), we can multiple \(\overline{\phi}_*\) and \(\overline{\psi}\) to both sides and integrate on \(\Omega\). This gives rise to \[\label{lin95sys} \left[ \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{matrix} \right] \left[ \begin{matrix} \beta_j \\ k_j \\ \gamma_j \end{matrix} \right] = \left[ \begin{matrix} b_{1j} \\ b_{2j} \end{matrix} \right],\tag{19}\] where \[\begin{align} && a_{1m} = \int_{\Omega} \overline{\phi}_* B_m d \mathbf{r}, \quad a_{2m} = \int_{\Omega} \overline{\psi} B_m d \mathbf{r}, \qquad m = 1, 2, 3 \\ && b_{1j} = \int_{\Omega} \overline{\phi}_* C_j d \mathbf{r}, \quad b_{2j} = \int_{\Omega} \overline{\psi} C_j d \mathbf{r}. \end{align}\] It is easy to check that \(a_{11}\), \(a_{12}\) and \(a_{13}\) are all real. From conditions (4 ) and (6 ), we obtain \(a_{22} = 0\) and \(a_{21} > 0\). The linear system (19 ) can be written as \[\label{lin95sys2} \left[ \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21}& 0 & Re(a_{23}) \\ 0 & 0 & Im(a_{23}) \end{matrix} \right] \left[ \begin{matrix} \beta_j \cr k_j \cr \gamma_j \end{matrix} \right] = \left[ \begin{matrix} b_{1j} \cr Re(b_{2j}) \cr Im(b_{2j}) \end{matrix} \right].\tag{20}\] Since \(F\) must satisfy condition (8 ), \(Im(a_{23}) \ne 0\). Therefore, the \(3 \times 3\) coefficient matrix above is invertible. To have real solutions for \(\beta_j\), \(k_j\) and \(\gamma_j\), we need to show that \(b_{1j}\) is real for all \(j \geq 1\).
For \(j=1\), \(C_1 = k_*^2 G \phi_*\). Since \(G\) is real, \(b_{11}\) is real. Meanwhile, since \(C_1\) decays exponentially as \(|z| \to \infty\), \(b_{21}\) is well defined. Therefore, we can find real \(\beta_1\), \(k_1\) and \(\gamma_1\). After that, we can solve \(\phi_1\) from Eq. (18 ) for \(j=1\). The solution \(\phi_1\) decays to zero as \(|z| \to \infty\) and has the same even/odd parity in \(z\) as \(\phi_*\).
For \(j=2\), \(C_2 = V_2 \phi_* + W_1 \phi_1 + 2 i \beta_1 \partial_y \phi_1\). It decays exponentially as \(|z| \to \infty\) and has the same even/odd parity as \(\phi_*\). Thus, \(b_{22}\) is well defined. Since \(V_2\) is real and \[b_{12} = \int_{\Omega} V_2 |\phi_*|^2 d \mathbf{r} + \int_{\Omega} \left( W_1 \phi_1 + 2i \beta_1 \partial_y \phi_1 \right) \overline{\phi}_* d \mathbf{r},\] it is only necessary to show the second term on the right hand side above is real. Multiplying the complex conjugate of Eq. (18 ) for \(j=1\) by \(\phi_1\) and integrating on \(\Omega\), we have \[\begin{align} \int_{\Omega} \phi_1 \overline{\mathcal{L} \phi_1} d \mathbf{r}&= & - \int_{\Omega} ( 2 k_* k_1 \varepsilon_* - 2 \beta_* \beta_1 + k_*^2 \gamma_1 F + V_1) \overline{ \phi}_* \phi_1 d \mathbf{r} + 2i \beta_1 \int_{\Omega} \phi_1 \partial_y \overline{\phi}_* d \mathbf{r} \\ & = & - \int_{\Omega} ( W_1 \phi_1 + 2 i \beta_1 \partial_y \phi_1) \overline{\phi}_* d \mathbf{r}. \end{align}\] It is easy to check that \(\int_{\Omega} \phi_1 \overline{\mathcal{L} \phi_1} d \mathbf{r}\) is real, thus \(b_{12}\) is real. Solving Eq. (20 ) for \(j=2\), we obtain real \(\beta_2\), \(k_2\) and \(\gamma_2\). After that, \(\phi_2\) can be solved from Eq. (18 ) for \(j=2\), and it decays to zero as \(|z| \to \infty\) and has the same even/odd parity as \(\phi_*\).
For \(j > 2\), we assume for any \(n\) satisfying \(1 \leq n \leq j-1\), \(\beta_n\), \(k_n\) and \(\gamma_n\) are real, \(\phi_n \to 0\) as \(|z| \to \infty\), and \(\phi_n\) has the same even/odd parity as \(\phi_*\). This implies that \(V_j\) and \(W_n\) for \(1 \leq n \leq j-1\) are real. Since \[b_{1j} = \int_{\Omega} \overline{\phi}_* C_j d \mathbf{r} = \int_{\Omega} V_j |\phi_*|^2 d \mathbf{r} + \sum\limits_{n=1}^{j-1} \int_{\Omega} \left( W_n \phi_{j-n} + 2 i \beta_n \partial_y \phi_{j-n} \right) \overline{\phi}_* d \mathbf{r},\] we only need to show the last term on the right hand side of above is real. Using the relations between \(W_n\) and \(V_n\) for \(1 \leq n \leq j-1\), we obtain \[\begin{align} \sum\limits_{n=1}^{j-1} \int_{\Omega} \phi_{j-n} \overline{\mathcal{L} \phi_n} d \mathbf{r} & = & -\sum_{n=1}^{j-1} \int_{\Omega} \left( W_n \phi_{j-n} + 2 i \beta_n \partial_y \phi_{j-n} \right) \overline{\phi}_* d \mathbf{r} \\ & - & \sum\limits_{n=1}^{j-2} \int_{\Omega} \left( \sum\limits_{m=n+1}^{j-1} \overline{\phi}_{m-n} \phi_{j-m} \right) W_n d \mathbf{r} + 2i \sum\limits_{n=1}^{j-2} \beta_n \int_{\Omega} \left( \sum\limits_{m=n+1}^{j-1} \phi_{j-m} \partial_y \overline{\phi}_{m-n} \right)d \mathbf{r} . \end{align}\] It is easy to verify that \(\sum\limits_{n=1}^{j-1} \int_{\Omega} \phi_{j-n} \overline{\mathcal{L} \phi_n} d \mathbf{r}\) and \(\sum\limits_{m=n+1}^{j-1} \overline{\phi}_{m-n} \phi_{j-m}\) for \(1 \leq n \leq j-1\) are real, and \(\sum\limits_{m=n+1}^{j-1} \phi_{j-m} \partial_y \overline{\phi}_{m-n}\) for \(1 \leq n \leq j-1\) are pure imaginary. Therefore, the first term on the right hand side of above is real, and \(b_{1j}\) is real.
2 S2: Special cases↩︎
If the BIC of the unperturbed structure is a standing wave, i.e., \(\beta_* = 0\), then we can choose \(\phi_*\) as a real function and \(\psi\) as a pure imaginary function. In that case, \(a_{11} = 0\), \(a_{21}\) is real, \(a_{23}\) and \(b_{2j}\) must be pure imaginary. The second equation of linear system Eq. (20 ) gives \(a_{21} \beta_j = 0\) for all \(j \ge 1\). Therefore, \(\beta_j = 0\) for all \(j \ge 1\).
If the unperturbed structure has a reflection symmetry in \(y\), i.e., \(\varepsilon_*\) satisfies \(\varepsilon_*({\boldsymbol{r}}) = \varepsilon_*(-y,z)\) for all \({\boldsymbol{r}}\), then, as shown in Ref. [37], we can scale the BIC and the diffraction solution such that \(\phi_*\) and \(\psi\) are \({\cal PT}\)-symmetric in \(y\), i.e., \[\label{PTiny} \phi_*({\boldsymbol{r}}) = \overline{\phi}_*(-y,z), \quad \psi({\boldsymbol{r}}) = \overline{\psi}(-y,z)\tag{21}\] for all \({\boldsymbol{r}}\). We still assume conditions (4 ) and (6 ) are satisfied, since they are consistent with the \({\cal PT}\)-symmetry scaling. If \(F\) is not symmetric in \(y\), then \(a_{23} = -k_*^2 \int_\Omega F \psi \phi_* d{\boldsymbol{r}}\) is in general complex, and we can assume condition (8 ) is satisfied. Therefore, the coefficient matrix in (20 ) is real and invertible. If \(G\) is symmetry in \(y\), then \(b_{21} = k_*^2 \int_\Omega G \overline{\psi} \phi_* d{\boldsymbol{r}}\) is real. Thus, linear system (20 ) gives a real \(\beta_1\), a real \(k_1\), and \(\gamma_1=0\). The right hand side of the governing equation for \(\phi_1\) does not involve \(F\) and is \(PT\)-symmetric. This implies that \(\phi_1\) and \(C_2\) are \({\cal PT}\)-symmetric. Repeating this process, we obtain \(\gamma_j = 0\) for all \(j \ge 1\).