Explaining Fast Improvement in Online Imitation Learning
July 06, 2020
Abstract
Online imitation learning (IL) is an algorithmic framework that leverages interactions with expert policies for efficient policy optimization. In this work, we provide an explanation of this phenomenon. Let \(\xi\) denote the policy class bias and assume the online IL loss functions are convex, smooth, and non-negative. We prove that, after \(N\) rounds of online IL with stochastic feedback, the policy improves in \(\tilde{O}(1/N + \sqrt{\xi/N})\) in both expectation and high probability. In other words, we show that adopting a sufficiently expressive policy class in online IL has two benefits: both the policy improvement speed increases and the performance bias decreases.
1 INTRODUCTION↩︎
Imitation learning (IL) is a framework for improving the sample efficiency of policy optimization in sequential decision making. Unlike reinforcement learning (RL) algorithms that optimize policies purely by trial-and-error, IL leverages expert policies in the training time to provide extra feedback signals to aid the policy search (e.g., in the form of supervised learning losses). These expert policies can represent human demonstrators or resource-intensive engineered solutions which achieve non-trivial performance in the problem domain. By following the guidance of an expert policy, the learner can avoid blindly exploring the problem space and focus on promising directions that lead to expert-like behaviors, so the learning becomes sample efficient.
Online IL, pioneered by [1], is one of the algorithms that exploit such expert policies. Given access to interact with an expert policy, online IL reduces policy optimization into no-regret online learning [2] for which effective algorithms have been developed. The main idea of online IL is to design an online learning problem1 of which 1) the decision set is identified with the policy class in the original policy optimization problem; and 2) the online loss functions are set to encourage the learner to take expert-like actions under its own state distribution, which resemble a sequence of supervised learning problems. When these two conditions are met, the reduction follows: the regret rate and the minimum cumulative loss witnessed in the online learning problem determine respectively the learning speed and the performance bias in the original policy optimization problem.
Since the seminal work by [1] was published, significant progress has been made in both theory and practice. It is shown that, for certain problems, online IL can learn the optimal policy exponentially faster than any RL algorithm when the expert policy is optimal [3]. Furthermore, online IL has been validated on physical robot control tasks [4], [5]. Beyond typical IL scenarios, online IL has also been applied to design algorithms for system identification [6], model-based RL [7], structured prediction [3], [8], [9], and combinatorial search [10]. Here we collectively call these algorithms online IL, since they adopt the same reduction idea and mainly differ in the way the expert policy is defined.
Despite the success of online IL, there is a mismatch between provable theoretical guarantees and the learning phenomenon observed in practice. Because of the design constraint imposed on the online losses mentioned above, the online losses used in the online IL reduction are not fully adversarial, but generated by samples of a sequence of probability distributions that vary slowly as the learner updates its policy [11]. This structure makes the performance guarantee given by the classic adversary-style analysis of the regret rate taken by [1] overly conservative, and motivates a deeper study on theoretical underpinnings of online IL [11]–[14].
In this work, we are interested in explaining the fast policy improvement of online IL that is observed in practice but not captured by existing theory. When the online loss functions are convex and Lipschitz, typical analyses of regret and martingales [1], [15] suggest an on-average convergence rate in \(O(1/\sqrt{N})\) after \(N\) rounds. However, empirically, online IL algorithms learn much faster; e.g., the online IL algorithm DAgger [1] learned to mimic a model predictive control policy for autonomous off-road driving in only three rounds in [5]. Although the convergence rate improves to \(\tilde{O}(1/N)\) when the online losses are strongly convex [11], this condition can be difficult to satisfy especially when the policy class is large, such as a linear function class built on high-dimensional features. The empirical effectiveness and sample efficiency of online IL demand alternative explanations.
Formally, we prove a new bias-dependent convergence rate for online IL that is adaptive to the performance of the best policy in the policy class on the sequence of sampled losses. Interestingly, this new rate shows that an online IL algorithm can learn faster as this performance bias becomes smaller. In other words, adopting a sufficiently expressive policy class in online IL has two benefits: as the policy class becomes reasonably rich, both the learning speed increases and the performance bias decreases.
Let \(\xi\) denote the policy class bias, . We give a convergence rate in \(\tilde{O}(1/N + \sqrt{\xi/N})\) both in expectation and in high probability for online IL algorithms using stochastic feedback. This new result shows a transition from the faster rate of \(\tilde{O}(1/N)\) to the usual rate of \(\tilde{O}(1/\sqrt{N})\) as the policy class bias \(\xi\) increases.
This type of bias-dependent or optimistic convergence rate has been studied in typical machine learning settings, e.g., statistical learning [16], stochastic convex optimization [17], [18], and online learning [16], [19]. indeed, previous analyses tackle only one of these two properties and a straightforward combination does not lead to the fast rate desired here (cf. 3.3). and leverage a recent martingale concentration result based on path-wise statistics [20].
We conclude by corroborating the new theoretical findings with experimental results of online IL. The detailed proofs for this paper can be found in the Appendix.
2 BACKGROUND: ONLINE IL↩︎
2.1 Policy Optimization↩︎
The objective of policy optimization is to find a high-performance policy in a policy class \(\Pi\) for sequential decision making problems. Typically, it models the world as a Markov decision process (MDP), defined by an initial state distribution, transition dynamics, and an instantaneous state-action cost function [21]. This MDP is often assumed to be unknown to the learning agent; therefore the learning algorithm for policy optimization needs to perform systematic exploration in order to discover good policies in \(\Pi\). Concretely, let us consider a policy class \(\Pi\) that has a one-to-one mapping to a parameter space \(\Theta\), and let \(\pi_\theta\) denote the policy associated with the parameter \(\theta \in \Theta\). That is, \(\Pi = \{\pi_\theta: \theta\in\Theta\}\). The goal of policy optimization is to find a policy \(\pi_\theta\in\Pi\) that minimizes the expected cost, \[\begin{align} \label{eq:rl32objective} J(\pi) \mathrel{\vcenter{:}}= \mathbb{E}_{s\sim d_{\pi_\theta}} \mathbb{E}_{a \sim \pi_\theta}[c(s, a)], \end{align}\tag{1}\] where \(s\) and \(a\) are the state and the action, respectively, \(c\) is the instantaneous cost function and \(d_{\pi_\theta}\) denotes the average state distribution over the problem horizon induced by executing policy \(\pi_\theta\) starting from a state sampled from the initial state distribution. The problem formulation in 1 applies to various settings of problem horizon and discount rate, where the main difference is how the average state distribution is defined; e.g., for a discounted problem, \(d_{\pi_\theta}\) is defined by a geometric mean, whereas \(d_{\pi_\theta}\) is the stationary state distribution for average infinite-horizon problems.
2.2 Online IL Algorithms↩︎
Online imitation learning (IL) is a policy optimization technique that leverages interactive experts to efficiently find good policies. It devises a sequence of online loss functions \({l}_n\) such that no regret and small policy class bias imply good policy performance in the original sequential decision problem.
Concretely, let \({\pi_\mathrm{e}}\) be an interactive expert policy. Instead of minimizing 1 directly, online IL minimizes the performance difference between the policy \(\pi_\theta\) and the expert \({\pi_\mathrm{e}}\): \[\begin{align} \label{eq:il32surrogate} J(\pi_\theta) - J({\pi_\mathrm{e}}) \leq O \Big( \underbrace{\mathbb{E}_{s \sim d_{\pi_\theta}} \mathbb{E}_{a \sim \pi_\theta}[D_{{\pi_\mathrm{e}}}(s,a)]}_{\text{{\color{black}{surrogate objective}}}} \Big), \end{align}\tag{2}\] where the function \(D_{\pi_\mathrm{e}}(s,a)\) represents how similar an action \(a\) is to the action taken by expert policy \({\pi_\mathrm{e}}\) at state \(s\), measured by statistical distances (e.g., Wasserstein distance and KL divergence) or their upper bounds [1], [3], [8]. Although the surrogate objective in 2 resembles 1 (i.e., by replacing \(D_{\pi_\mathrm{e}}(s,a)\) with \(c(s,a)\)), the surrogate objective has an additional , if the policy class \(\Pi\) has enough capacity to contain the expert policy \({\pi_\mathrm{e}}\), there is a policy \(\pi_\theta \in \Pi\) such that, for all states, \[\begin{align} \label{eq:realizable32assumption} \mathbb{E}_{a \sim \pi_\theta}[D_{{\pi_\mathrm{e}}}(s,a)] =0. \end{align}\tag{3}\] online IL can minimize the surrogate function in 2 by solving an online learning problem: Let parametric space \(\Theta\) be the decision set (i.e., the policy class) in online learning; it defines the online loss function in round \(n\) as \[\begin{align} \label{eq:IL32online32loss} {{l}_n(\theta)}=\mathbb{E}_{s \sim d_{\pi_{\theta_n}}} \mathbb{E}_{a \sim \pi_\theta}[D_{{\pi_\mathrm{e}}}(s, a)], \end{align}\tag{4}\] where \(\theta_n\in\Theta\) is the online decision made by the online algorithm in round \(n\).
The main benefit of this indirect approach is that, compared with the surrogate function 2 , the average state distribution \(d_{\pi_{\theta_n}}\) in the online loss function 4 is not considered as a function of the policy parameter \(\theta\), making the online loss function 4 the objective function of a supervised learning problem whose sampled gradient is less noisy than that of the surrogate problem in 2 . Because of the 3 , the influence of the policy parameter on the change of the average state distribution can be ignored here, and the average regret with respect to the online loss functions in 4 alone [1] can upper bound the surrogate function in 2 .
When the expert policy \({\pi_\mathrm{e}}\) is only nearly realizable by the policy class \(\Pi\) (that is, 3 can only be satisfied up to a certain error), optimizing the policy with this online learning reduction would suffer from an extra performance bias due to using a limited policy class, as we will later discuss in 2.3.

Figure 1: Online Imitation Learning (IL)
2.2.0.1 Summary
Online IL can be viewed as a meta algorithm shown in 1, where we take into account that in practice the MDP is unknown and therefore the online loss function \({l}_n\) needs to be further approximated by finite samples as \({\hat{l}}_n\), such that \(\forall\theta\in\Theta\), \(\mathbb{E}[{\hat{l}}_n(\theta)] = {l}_n(\theta)\). Given an expert policy, it selects a surrogate function to satisfy conditions similar to 2 and 3 (or their approximations). Then a no-regret online learning algorithm \(\mathcal{A}\) is used to optimize the policy with respect to the sampled online loss functions \({\hat{l}}_n\), generating a sequence of policies \(\{\pi_{\theta_n}\}_{n=1}^N\). By this reduction, performance guarantees can be obtained for the best policy in this sequence.
2.2.0.2 Online IL in General
Before proceeding we note that by following the online IL design protocol above, 1 can be instantiated beyond the typical IL setup. By properly choosing the definition of expert policies, the online IL reduction can be used to efficiently solve model-based RL and system identification where the samples of the MDP transition dynamics are treated as experts demonstrations [6], [7], and structured prediction where expert state-action value functions measure how good an action is in the surrogate function in 2 [3], [8].
2.3 Guarantees of Online IL↩︎
Now that we have reviewed the algorithmic aspects of online IL, we give a brief tutorial of the theoretical foundation of online IL and the known convergence results, which show exactly how regret and policy class bias are related to the performance in the original policy optimization problem.
To this end, let us formally define 1) the regret and 2) the policy class bias. For a sequence of online loss functions \(\{f_n\}_{n=1}^N\) and decisions \(\{\theta_n\}_{n=1}^N\) in an online learning problem, we define the regret as \[\begin{align} \label{eq:regret} \textstyle \textrm{Regret}(f_n) = \sum f_n(\theta_n) - \min_{\theta \in \Theta} \sum f_n(\theta). \end{align}\tag{5}\] Note that, for brevity, the range in \(\sum_{n=1}^N\) is omitted in 5 and we will continue to do so below as long as the range is clear from the context. In addition to the regret, we define two problem-dependent biases of the decision set \(\Theta\) (the equivalence of the policy class \(\Pi\)).
Definition 1 (Problem-dependent biases). For the sampled loss functions \(\{{\hat{l}}_n\}_{n=1}^N\) experienced by running 1, we define \({\hat{\epsilon}}= \frac{1}{N}\min_{\theta \in \Theta} \sum {{\hat{l}}_n(\theta)}\) and \({\epsilon}= \frac{1}{N}\min_{\theta \in \Theta} \sum {{l}_n(\theta)}\), where for all \(n\) and \(\theta\), \({{l}_n(\theta)}= \mathbb{E}[{{\hat{l}}_n(\theta)}]\).
A typical online IL analysis uses the regret and the policy class biases \({\epsilon}\) and \({\hat{\epsilon}}\) to decompose the cumulative loss \(\sum {{l}_n(\theta_n)}\) to provide policy performance guarantees. Specifically, define \(\theta^\star \in \mathop{\mathrm{arg\,min}}_{\theta \in \Theta} \sum l_n(\theta)\). By 5 and 1, we can write \[\begin{align} \textstyle \sum {{l}_n(\theta_n)} & \textstyle = {\textrm{Regret}({\hat{l}}_n)}+ \left( \sum {{l}_n(\theta_n)}- {{\hat{l}}_n(\theta_n)} \right) + N{\hat{\epsilon}}\tag{6} \\ & \textstyle \le {\textrm{Regret}({\hat{l}}_n)}+ \left( \sum {{l}_n(\theta_n)}- {{\hat{l}}_n(\theta_n)} \right) + \nonumber \\ & \; \; \; \left( \sum {\hat{l}}_n(\theta^\star) - {l}_n(\theta^\star) \right) + N{\epsilon}\tag{7} \end{align}\] where, in both 6 and 7 , the first term is the online learning regret, the middle term(s) are the generalization error(s), and the last term is the policy class bias.
In a nutshell, existing convergence results of online IL are applications of 6 and 7 with different upper bounds on the regret and the generalization errors [1], [3], [7], [8]. For example, when the sampled loss functions \({\hat{l}}_n\) are bounded, the generalization error(s) (i.e., the middle term(s) in 6 and 7 ) can be bounded by \(\tilde{O}(\sqrt{N})\) with high probability by Azuma’s inequality (see [15] or [2]). Together with an \(O(\sqrt{N})\) bound on the regret (which is standard for online convex losses) [2], [22], it implies that the average performance \(\frac{1}{N} \sum {{l}_n(\theta_n)}\) and the best performance \(\min_n {{l}_n(\theta_n)}\) converge to \({\hat{\epsilon}}\) or \({\epsilon}\) at the speed of \(\tilde{O}(1/\sqrt{N})\).
However, the rate above often does not explain the fast improvement of online IL observed in practice [3], [5], [23], [24], as we will also show experimentally in 5. While faster rates in \(\tilde{O}(1/N)\) was shown for strongly convex loss functions [1], [11], the strong convexity assumption usually does not hold; . Thus, alternative explanations are needed.
3 NEW BIAS-DEPENDENT RATES↩︎
In this section, we present new policy convergence rates that are adaptive to the performance biases in 1. The full proof of these theorems is provided in the Appendix.
3.1 Setup and Assumptions↩︎
We suppose the parameter space of the policy class \(\Theta\) is a closed convex subset of a Hilbert space \(\mathcal{H}\) that is equipped with norm \(\| \cdot \|\). Since \(\| \cdot \|\) is not necessarily the norm induced by the inner product, we denote its dual norm by \(\| \cdot \| _*\), which is defined as \(\| x \| _* = \max_{\| y \| =1} \langle x, y\rangle\).
We define admissible algorithms to broaden the scope of online IL algorithms that our analysis covers.
Definition 2 (Admissible online algorithm). We say an online algorithm \(\mathcal{A}\) is admissible for a parameter space \(\Theta\) if there exists \(R_\mathcal{A}\in[0,\infty)\) such that given any \(\eta > 0\) and any sequence of differentiable convex functions \(f_n\), \(\mathcal{A}\) can achieve \(\textrm{Regret}(f_n) \le \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) \le \frac{1}{\eta} R_\mathcal{A}^2 + \frac{\eta}{2}\sum \| {\nabla f_n(\theta_n)} \| _*^2\), where \(\theta_n\) is the decision made by \(\mathcal{A}\) in round \(n\).
We assume that 1 is realized by an admissible online learning algorithm \(\mathcal{A}\). This assumption is satisfied by common online algorithms, such as mirror descent [25] and Follow-The-Regularized-Leader [22], where \(\eta\) in 2 corresponds to a constant stepsize that is chosen before seeing the online losses, and \(R_\mathcal{A}\) measures that size of the decision set \(\Theta\). Finally, we formally define convex, smooth, and non-negative (CSN) functions; we will assume the online loss \({l}_n\) in online IL and its sampled version \({\hat{l}}_n\) belong to this class.
Definition 3 (Convex, smooth, and non-negative (CSN) function). A function \(f: \mathcal{H}\to \mathbb{R}\) is CSN if \(f\) on \(\mathcal{X}\) is convex, \(\beta\)-smooth2, and non-negative.
Several popular loss functions used in online IL (e.g., squared \(\ell_2\)-loss and KL-divergence) are indeed CSN (3) (see 4 for examples). If the losses are not smooth, several smoothing techniques in the optimization literature are available to smooth the losses locally, e.g., Nesterov’s smoothing [26], Moreau-Yosida regularization [27], and randomized smoothing [28].
3.2 Rate in Expectation↩︎
theoremthmexpectation In 1, suppose \({\hat{l}}_n\) is CSN and \(\mathcal{A}\) is admissible. Let \({\hat{\epsilon}}= \frac{1}{N}\min_{\theta \in \Theta} \sum {{\hat{l}}_n(\theta)}\) be the bias, and let \({\hat{E}}\) be an upper bound on \({\hat{\epsilon}}\). \(\frac{1}{2\left(\beta + \sqrt{\beta^2 + \frac{1}{2} \beta N {\hat{E}}R_\mathcal{A}^{-2} } \right)}\). Then it holds that \[\begin{align} \label{eq:rate32in32expectation} \textstyle \mathbb{E}\left[\frac{1}{N}\sum {{l}_n(\theta_n)}- {\hat{\epsilon}}\right] \le \frac{8 \beta R_\mathcal{A}^2}{N} + \sqrt{\frac{8\beta R_\mathcal{A}^2 {\hat{E}}}{N}} \end{align}\tag{8}\]
The rate in 8 suggests that an online IL algorithm can learn faster as the policy class bias becomes smaller; this is reflected in the transition from the usual rate \(O(1/\sqrt{N})\) to the faster rate \(O(1/N)\) when the bias goes to zero. Notably, the rate in 8 does not depend on the dimensionality of \(\mathcal{H}\) but only on \(R_\mathcal{A}\), which one can roughly think of as the largest norm in \(\Theta\). Therefore, we can increase the dimension of the policy class to reduce the bias (e.g., by using reproducing kernels [29]) as long as the diameter of \(\Theta\) measured by norm \(\| \cdot \|\) (e.g., \(\ell_2\)-norm) stays controlled.
3.2.0.1 Online IL with Adaptive Stepsizes
3.3 Rate in High Probability↩︎
Next we show that a similar 3 bias-dependent convergence rate to the rate 8 also holds in high probability.
theoremthmhighprob Under the same assumptions and setup of [thm:rough32bound32in32expectation], further assume that there is \(G\in[0,\infty)\) such that, for any \(\theta \in \Theta\), \(\| \nabla {\hat{l}}_n(\theta) \| _* \le G\). For any \(\delta < 1/e\), with probability at least \(1-\delta\), the following holds \[\begin{align} \label{eq:rate32with32high32probability} \textstyle \frac{1}{N}\sum {{l}_n(\theta_n)}- {\epsilon}= O \left( \frac{C \beta R^2}{N} + \sqrt{\frac{C \beta R^2 ({\hat{E}}+ {\epsilon})}{N}} \right) \end{align}\tag{9}\] where \(R_\Theta = \max_{\theta \in \Theta} \| \theta \| , R = \max(1, R_\Theta, R_\mathcal{A}), C = \log(1/\delta) \log(G R N)\).
We remark that the uniform bound \(G\) on the norm of the gradients only appears in logarithmic terms. Therefore, this rate stays reasonable when the loss functions have gradients whose norm grows with the size of \(\Theta\), such as the popular squared loss.
To prove [thm:rough32bound32in32high32probability], one may attempt to build on top of the proof of [thm:rough32bound32in32expectation] by applying basic martingale concentration properties on the martingale difference sequences (MDSs) in 6 , or devise a similar scheme for 7 . But taking this direct approach will bring back the usual rate of \(O(1/\sqrt{N})\). To the best of our knowledge, sharp concentration inequalities for the counterparts of MDS in other learning settings cannot be adapted here in a straightforward way. [16] prove a fast rate for empirical risk minimizer (ERM) in statistical learning. However, their proof is based on local Rademacher complexities, which do not have obvious extension to non-stationary online losses. [17] extend the results of [16] to stochastic convex optimization, but the extension relies on an i.i.d. concentration lemma.4 [31] show fast converging excess risk of online convex programming algorithms when the loss function is Lipschitz and strongly convex; relaxing the strong convexity assumptions is the goal of this work.
3.3.0.1 Convexity Assumption
| Setting | Info. | Stochastic | Non-stationary | Partial FB | Estimator | Excess loss to minimize |
|---|---|---|---|---|---|---|
| Online IL (this work) | \({\hat{l}}_n\) | Yes | Yes | No | Online | \(\sum {l}_n (\theta_n) - \min \sum {l}_n(\theta)\) |
| Stochastic bandits | \({\hat{l}}(\theta_n)\) | Yes | No | Yes | Online | \(\sum {l}(\theta_n) - N \min {l}(\theta)\) |
| Online learning | \({l}_n\) | No | Yes | No | Online | \(\sum {l}_n(\theta_n) - \min \sum {l}_n(\theta)\) |
| Statistical learning | \({\hat{l}}\) | Yes | No | No | ERM | \({l}(\theta_{\mathrm{ERM}}) - \min {l}(\theta)\) |
| Online-to-batch | \({\hat{l}}\) | Yes | No | No | Online | \(\sum l(\theta_n) - N \min l(\theta)\) |
3.3.0.2 Related Work in Learning
Similar bias-dependent or optimistic rates have been studied extensively in several more typical learning settings such as contextual bandits [32], statistical learning [16]–[18], [33], online learning with adversarial loss sequences [16], [34], and online-to-batch conversion [15], [35].
3.3.0.3 Specialization to Stochastic Convex Optimization
Because of the generality of the online IL, an online IL algorithm (1) running on a stationary loss function can serve as a one-pass learning algorithm for stochastic optimization; that is, we have \({l}_n = {l}\) for some \({l}\) for all \(n\); By specializing [thm:rough32bound32in32expectation] and [thm:rough32bound32in32high32probability] to the stochastic optimization setting, we can recover the existing bounds in the stochastic optimization literature, i.e., Corollary 3 and Theorem 1 in [16], respectively. These special cases can be derived in a straightforward manner due to the relationship between \({\hat{\epsilon}}\) and \({\epsilon}\) when the loss function is fixed (i.e., \({l}_n = {l}\)): 1) \(\mathbb{E}[\epsilon] = \mathbb{E}[{\hat{\epsilon}}]\), and 2) in high probability, \({\hat{\epsilon}}- {\epsilon}\le O(\sqrt{1/N})\). However, we note that for general online IL problems, the sizes of \({\hat{\epsilon}}\) and \({\epsilon}\) are not comparable and \(\mathbb{E}[\epsilon] \neq \mathbb{E}[{\hat{\epsilon}}]\).
3.4 Proof Sketch for Theorem 2↩︎
We take a different decomposition of the cumulative loss to avoid the usual \(O(1/\sqrt{N})\) rate originating from applying martingale analyses on the MDSs in 6 and 7 . Here we construct two new MDSs in terms of the gradients: recall \({\epsilon}= \min_{\theta \in \Theta} \sum {{l}_n(\theta)}\) and let \(\theta^\star = \mathop{\mathrm{arg\,min}}_{\theta \in \Theta} \sum {{l}_n(\theta)}\). Then by convexity of \({l}_n\), we can derive \[\begin{align} \label{eq:proof32first} & \quad \sum {{l}_n(\theta_n)}- N {\epsilon}\nonumber \\ & \le \sum \underbrace{\langle {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}, \theta_n \rangle}_{\text{MDS}} - \\ & \;\;\; \;\; \sum \langle \underbrace{{\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}}_{\text{MDS}}, \theta^\star \rangle + \textrm{Regret}(\langle\nabla {\hat{l}}_n(\theta_n), \cdot\rangle) \nonumber \end{align}\tag{10}\]
Our proof is based on analyzing these three terms. For the MDSs in 10 , we notice that, for smooth and non-negative functions, the squared norm of the gradients can be bounded by its function value.
lemmaselfbounding Suppose a function \(f: \mathcal{H}\to \mathbb{R}\) is \(\beta\)-smooth and non-negative, then for any \(x \in \mathcal{H}\), \(\| \nabla f(x) \| _*^2 \le 4 \beta f(x)\).
[lm:self32bounding] enables us to properly control the second-order statistics of the MDSs in 10 . By a recent vector-valued martingale concentration inequality that depends only on second-order statistics [20], we obtain a self-bounding property for 10 to get fast concentration rate.
Besides analyzing the MDSs, we need to bound the regret to the linear functions defined by the gradients (the last term in 10 ). Since this last term is linear, not CSN, the bias-dependent online regret in the proof of [thm:rough32bound32in32expectation] does not apply. Nonetheless, because these linear functions are based on the gradients of CSN functions, we discover that their regret rate actually obeys the exact same rate as the regret to the CSN loss functions. This is notable because the regret to these linear functions upper bounds the regret to the CSN loss functions.
Combining the bounds on the MDSs and the regret, we obtain the rate in 9 .
4 CASE STUDIES↩︎
We use two concrete instantiations of the online IL algorithm (1) to show how the new theoretical results in 3 improve the existing understanding of the policy improvement speed in these algorithms.
4.1 Imitation Learning↩︎
The seminal work on online IL [1] has demonstrated successes in solving many real-world sequential decision making problems [5], [23], [36]. When the action space is discrete, a popular design choice is to set \(D_{{\pi_\mathrm{e}}}(s,a)\) in 4 as the hinge loss [1]. For continuous domains, \(\ell_1\)-loss becomes a natural alternative for defining \(D_{{\pi_\mathrm{e}}}(s,a)\), which, e.g., is adopted by [5] for autonomous driving. When the policy is linear in the parameters, one can verify that these loss functions are convex and non-negative, though not strongly convex. Therefore, existing theorems suggest only an \(O(1/\sqrt{N})\) rate, which does not reflect the fast experimental rates [1], [5].
Although our new theorems are not directly applicable to these non-smooth loss functions, they can be applied to a smoothed version of these non-negative convex loss functions. For instance, applying the Huber approximation (an instantiation of Nesterov’s smoothing) [26] to “smooth the tip” of these \(\ell_1\)-like losses yields a globally smooth function with respect to the \(\ell_2\)-norm. As the smoothing mainly changes where the loss is close to zero, our new theorems suggest that, when the policy class is expressive enough, learning with these \(\ell_1\)-like losses would converge in a \(\tilde{O}(1/N)\) rate before the policy gets very close to the expert policy during policy optimization.
4.2 Interactive System ID for Model-based RL↩︎
Interactive system identification (ID) is a technique that interleaves data collection and dynamics model learning for robust model-based RL. [7] show that interactive system ID can be analyzed under the online IL framework, where the regret guarantee implies learning a dynamics model that mitigates the train-test distribution shift problem [7], [37]. Let \(T\) and \(T_\theta\) denote the true and the learned transition dynamics, respectively. A common online loss for interactive system ID is \({{l}_n(\theta)}= \mathbb{E}_{(s,a) \sim \frac{1}{2}{d_{T_{\theta_{n}}}} + \frac{1}{2}\nu } \left[ D_{s,a}(T_\theta|| T) \right]\), where \(D_{s,a}(T_\theta|| T)\) is some distance between \(T\) and \(T_\theta\) under state \(s\) and action \(a\), \(\nu\) is the state-action distribution of an exploration policy, and \(d_{T_{\theta_{n}}}\) is the state-action distribution induced by running an optimal policy with respect to the model \(T_{\theta_n}\). When the model class is expressive enough to contain the \(T\), it holds \({{l}_n(\theta)}=0\) for some \(\theta\in\Theta\) (cf. 3 ).
Suppose that the states and actions are continuous. A common choice for \(D_{s,a}(T_\theta|| T)\) in learning deterministic dynamics is the squared error \(D_{s,a}(T_\theta|| T)= \| T_\theta(s,a)- s' \| _2^2\) [7], where the \(s'\) is the next state in the true transition of \(T\). If \(T_\theta\) is linear in \(\theta\) or belongs to a reproducing kernel Hilbert space, the sampled loss function \({\hat{l}}_n\) is CSN. Alternatively, when learning a probabilistic model, \(D_{s,a}\) can be selected as the KL-divergence [7]; it is known that if \(T_\theta\) belongs to the exponential family of distributions, the KL divergence, and hence \({\hat{l}}_n\), are smooth and convex [38]. If the sample size is large enough, \({\hat{l}}_n\) becomes non-negative in high probability.
As these online losses are CSN, our theoretical results apply and suggest a convergence rate in \(\tilde{O}(1/N)\). On the contrary, the finite sample analysis conducted in [7] uses the standard online-to-batch techniques [15] and can only give a rate of \(O(1/\sqrt{N})\). Our new results provide a better explanation to justify the fast policy improvement speed observed empirically, e.g., [7].
5 EXPERIMENTAL RESULTS↩︎
Although the main focus of this paper is the new theoretical insights, we conduct experiments to provide evidence that the fast policy improvement phenomenon indeed exists, as our theory predicts. We verify the change of the policy improvement rate due to policy class capacity by running an imitation learning experiment in a simulated CartPole balancing task. Details can be found in 10.
5.0.0.1 MDP setup
The goal of the CartPole task is to keep the pole upright by controlling the acceleration of the cart. The start state is a configuration with a small uniformly sampled offset from being static and vertical, and the dynamics is deterministic. In each time step, if the pole is maintained within a threshold from being upright, the learner receives an instantaneous reward of one; otherwise, the learner receives zero rewards and the episode terminates. This MDP has a 4-dimensional continuous state space and a 1-dimensional continuous action space.
5.0.0.2 Expert and learner policies
We use a neural network expert policy (with one hidden layer of \(64\) units and \(\mathrm{tanh}\) activation) which is trained using policy gradient with GAE [39] and ADAM [40]. We let the learner policy be another neural network that shares the same architecture with the expert policy.
5.0.0.3 Online IL setup
We emulate online IL with unbiased and biased policy classes. We select \({l}_n(\theta) = \mathbb{E}_{s \sim d_{\pi_{\theta_n}}} [H_\mu(\pi_\theta(s) - {\pi_\mathrm{e}}(s))]\) as the online loss in IL (see 2.2), where \(H_\mu\) is the Huber function defined as \(H_\mu(x) = \frac{1}{2} x^2\) for \(| x | \le \mu\) and \(\mu | x | - \frac{1}{2}\mu^2\) for \(| x | > \mu\). In the experiments, \(\mu\) is set to \(0.05\); as a result, \(H_\mu\) is linear when its function value is larger than \(0.00125\). , because the learner’s policy is linear, this online loss is CSN (3) in the unknown weights of the learner.
5.0.0.4 Simulation results
We compare the results in the unbiased and the biased settings, in terms of how the average loss \(\frac{1}{N}\sum_{n=1}^N {{l}_n(\theta_n)}\) changes as the number of rounds \(N\) in online learning increases.
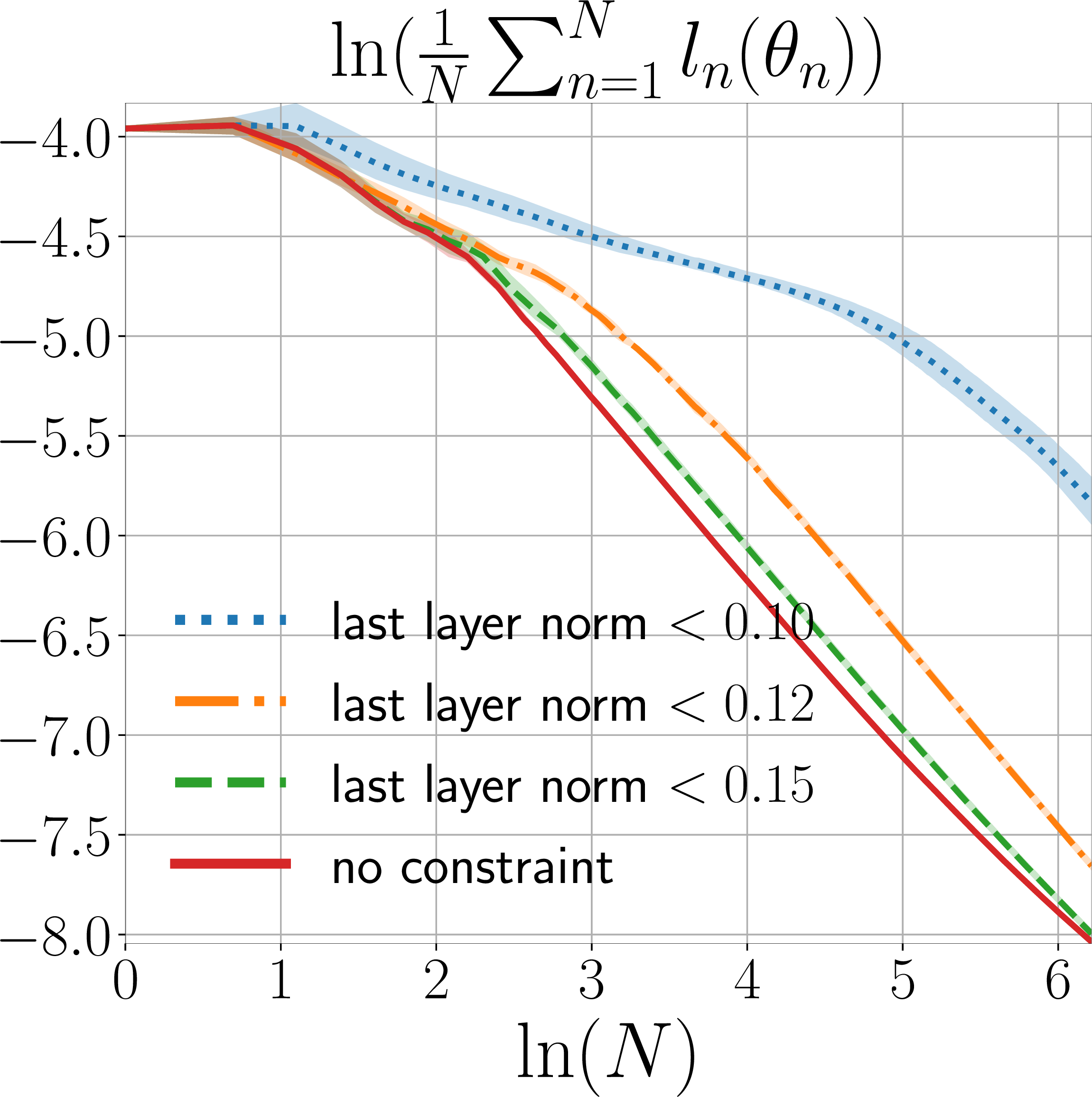
learning output layer
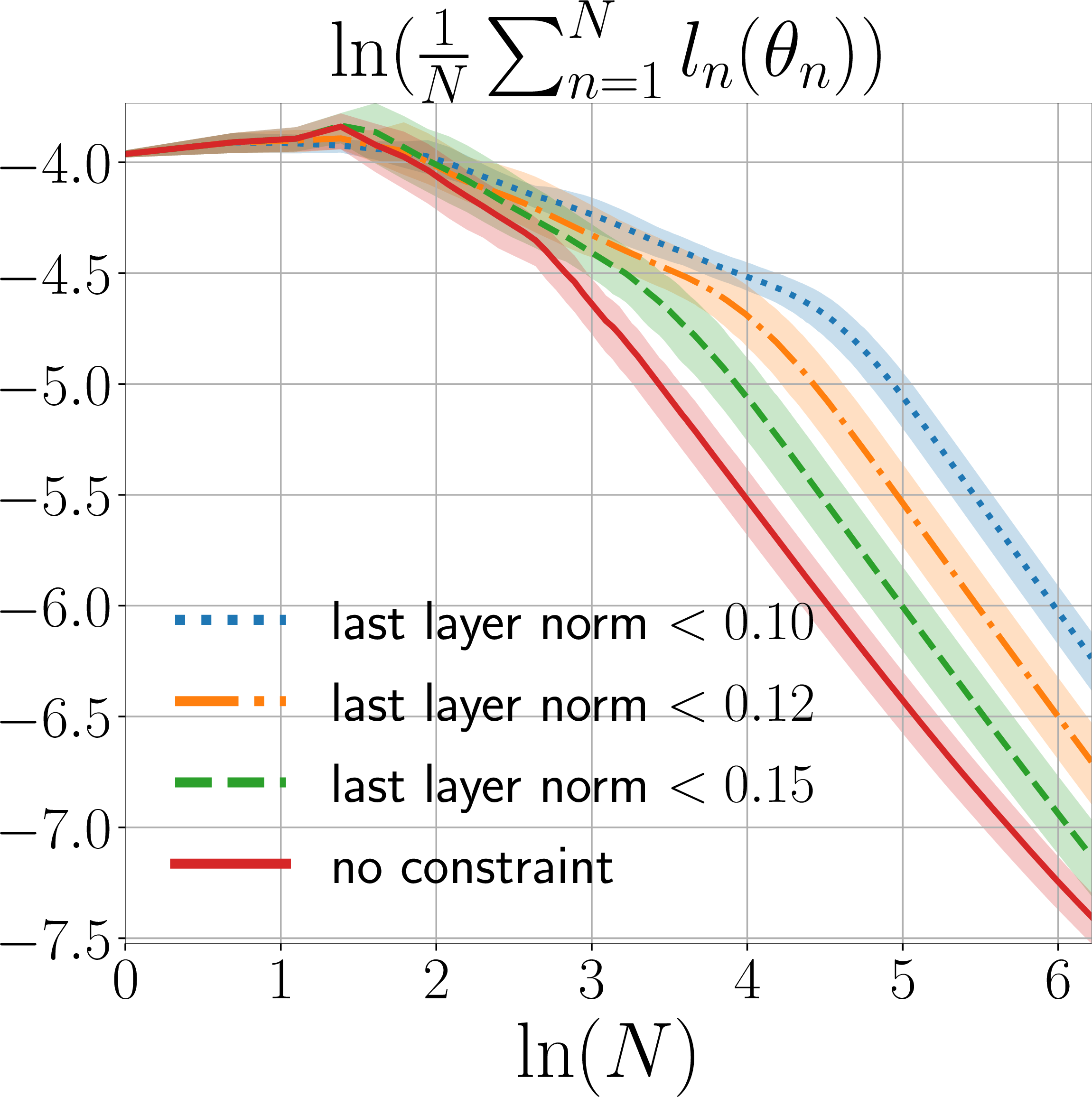
learning full network
Figure 2: The convergence rate of online IL with different policy class biases, where the bias is defined as the \(\ell_2\)-norm constraint on the weights of the output layer. The curves are plotted using the median over 4 random seeds, and the shaded region represents \(10\%\) and \(90\%\) percentile..
6 CONCLUSION↩︎
In this paper, we provide an explanation of the fast learning speed of online IL by proving new expected and high-probability convergence rates that depend on the policy class capacity. However, our current results do not explain all the fast improvements of online IL observed in practice. The analyses here are based on the assumption of using convex and smooth loss functions. This assumption would be violated, for example, with a deep neural network policy based on with ReLU activation; yet [5] show fast empirical convergence rates of these networks in online IL. Nonetheless, we envision that the insights from this paper can provide a promising direction to better understanding the behaviors of online IL, and to suggest ways for designing new online IL algorithms that proactively leverage these self-bounding regret properties to achieve faster learning.
7 PROOF OF TOOL LEMMAS↩︎
7.1 Proof of Lemma 1↩︎
For completeness, we provide the proof for the basic inequality that upper bounds the norm of gradients by the function values, for smooth and nonnegative functions. This is essential for obtaining the self-bounding properties for proving 1 and [thm:rough32bound32in32high32probability] later on.
Proof. Fix any \(x \in \mathcal{H}\). And fix any \(y \in \mathcal{H}\) satisfying \(\| y-x \| \le 1\). Let \(g(u) = f(x + u(y-x))\) for any \(u \in \mathbb{R}\). Fix any \(u, v \in \mathbb{R}\), \[\begin{align} |g'(v) - g'(u)| & = |\langle \nabla f(x+v(y-x)) - \nabla f(x+u(y-x)), y - x\rangle| \\ & \le \|\nabla f(x+v(y-x)) - \nabla f(x+u(y-x)) \|_* \| y - x\| \\ & \le \beta |v-u|\|y - x\|^2 \\ & \le \beta |v-u| \end{align}\] Hence, \(g\) is \(\beta\)-smooth. By the mean-value theorem, for any \(u, v \in \mathbb{R}\), there exists \(w \in (u, v)\), such that \(g(v) = g(u) + g'(w) (v-u)\). Hence \[\begin{align} 0 & \le g(v) = g(u) + g'(u)(v-u) + (g'(w) - g'(u))(v-u) \\ & \le g(u) + g'(u)(v-u) + \beta |w-u| |v-u| \le g(u) + g'(u)(v-u) + \beta (v-u)^2 \end{align}\] Setting \(v = u - \frac{g'(u)}{2\beta}\) yields that \(|g'(u)| \le \sqrt{4\beta g(u)}\). Therefore, we have \[\begin{align} |g'(0)| = |\langle \nabla f(x), y - x\rangle| \le \sqrt{4\beta g(0)} = \sqrt{4 \beta f(x)} \end{align}\] Therefore, by the definition of dual-norm, \[\begin{align} \| \nabla f(x) \| _* = \sup_{y\in \mathcal{B}, \| y-x \| \le 1} \langle \nabla f(x), y-x \rangle = \sup_{y\in \mathcal{B}, \| y-x \| \le 1} |\langle \nabla f(x), y-x \rangle |\le \sqrt{4 \beta f(x)} \end{align}\] where the second equality is due to the domain of \(y-x\). ◻
It’s worthy to note that \(f\) needs to be smooth and non-negative on the entire Hilbert space \(\mathcal{H}\).
8 PROOF OF THEOREM 1↩︎
The rate 8 follows from analyzing the regret and the generalization error in the decomposition in 6 . First, under the assumption of CSN loss functions and admissible online algorithms, the online regret can be bounded by an extension of the bias-dependent regret that is stated for mirror descent in [16], whose average gives the rate in 8 (see 8.1). Second, the generalization error in 6 vanishes in expectation because it is a martingale difference sequence (see 8.2).
8.1 Upper Bound of Online Regret↩︎
We show a bias-dependent regret of admissible online algorithms (2) with CSN functions (3) by extending Theorem 2 of [16] as follows.
Lemma 1. Consider running an admissible online algorithm \(\mathcal{A}\) on a sequence of CSN loss functions \(\{f_n\}\). Let \(\{\theta_n\}\) denote the online decisions made in each round, and let \({\hat{\epsilon}}= \frac{1}{N}\min_{\theta \in \Theta} \sum f_n(\theta)\) be the bias, and let \({\hat{E}}\) be such that \({\hat{E}}\geq {\hat{\epsilon}}\) almost surely. Choose \(\eta\) for \(\mathcal{A}\) to be \(\frac{1}{2 \left( \beta + \sqrt{\beta^2 + \frac{\beta N {\hat{E}}}{2 R_\mathcal{A}^2}} \right) }\). Then the following holds \[\begin{align} \textrm{Regret}(f_n) \le 8 \beta R_\mathcal{A}^2 + \sqrt{8\beta R_\mathcal{A}^2 N {\hat{E}}}. \end{align}\]
Proof. Because the online algorithm \(\mathcal{A}\) is admissible, we have \[\begin{align} \textrm{Regret}(f_n) \le \frac{1}{\eta} R_\mathcal{A}^2 + \frac{\eta}{2}\sum \| {\nabla f_n(\theta_n)} \| _*^2 \end{align}\] Let \(\lambda = \frac{1}{2\eta}\) and \(r^2 = 2R_\mathcal{A}^2\), then \[\begin{align} \frac{1}{\eta} R_\mathcal{A}^2 + \frac{\eta}{2}\sum \| {\nabla f_n(\theta_n)} \| _*^2 = \lambda r^2 + \sum \frac{1}{4\lambda}\| {\nabla f_n(\theta_n)} \| _*^2 \end{align}\] Using [lm:self32bounding] yields a self-bounding property for \(\textrm{Regret}(f_n)\): \[\begin{align} \label{eq:concrete32self-bounding} \textrm{Regret}(f_n) \le \lambda r^2 + \frac{\beta}{\lambda} \sum f_n(\theta_n) \le \lambda r^2 + \frac{\beta}{\lambda} \textrm{Regret}(f_n) + \frac{\beta}{\lambda} N {\hat{E}} \end{align}\tag{11}\] By rearranging the terms, we have a bias-dependent upper bound \[\begin{align} \label{eq:proof32thm132bound} \textrm{Regret}(f_n) \le \frac{\beta}{\lambda - \beta} N{\hat{E}}+ \frac{\lambda^2}{\lambda - \beta} r^2 \end{align}\tag{12}\] The upper bound can be minimized by choosing an optimal \(\lambda\). Setting the derivative of the right-hand side to zero, and computing the optimal \(\lambda\) (\(\lambda > 0\)) gives us \[\begin{align} \label{eq:lambda} r^2 \lambda^2 - 2 \beta r^2 \lambda - \beta N {\hat{E}}= 0, \quad \lambda > 0 \quad \text{ and } \quad \lambda = \beta + \sqrt{\beta^2 + \frac{\beta N {\hat{E}}}{r^2}} \end{align}\tag{13}\] which implies that the optimal \(\eta\) is \(\frac{1}{2 \left( \beta + \sqrt{\beta^2 + \frac{\beta N {\hat{E}}}{2 R_\mathcal{A}^2}} \right) }\). Since the optimal \(\lambda\) satisfies \(\beta N {\hat{E}}= r^2 \lambda^2 - 2 \beta r^2 \lambda\) implied from 13 , 12 can be simplified into: \[\begin{align} \textrm{Regret}(f_n) & \le \frac{1}{\lambda-\beta} \beta N {\hat{E}}+ \frac{\lambda^2}{\lambda - \beta} r^2 = \frac{1}{\lambda - \beta}(r^2 \lambda^2 - 2 \beta r^2 \lambda) +\frac{\lambda^2}{\lambda - \beta} r^2 \nonumber \\ & =\frac{2\lambda^2 r^2 - 2\beta \lambda r^2}{\lambda - \beta} = 2 \lambda r^2 \end{align}\] Plugging in the optimal \(\lambda\) yields \[\begin{align} \label{eq:ol32result} \textrm{Regret}(f_n) & \le 2 \lambda r^2 = 2 \left( \beta + \sqrt{\beta^2 + \frac{\beta N{\hat{E}}}{r^2}} \right) r^2\nonumber \\ & = 2 \beta r^2 + \sqrt{2\beta r^2} \sqrt{2\beta r^2 + 2N{\hat{E}}} \nonumber \\ & \le 4 \beta r^2 + 2 \sqrt{\beta r^2 N {\hat{E}}} \nonumber \\ & = 8 \beta R_\mathcal{A}^2 + \sqrt{8\beta R_\mathcal{A}^2 N {\hat{E}}} \end{align}\tag{14}\] where the last inequality uses the basic inequality: \(\sqrt{a+b}\leq\sqrt{a}+\sqrt{b}\). ◻
Notably, the admissibility defined in 2 is satisfied by common online algorithms, such as mirror descent [25] and Follow-The-Regularized-Leader [22] under first-order or full-information feedback, where \(\eta\) in 2 corresponds to a constant stepsize, and \(R_\mathcal{A}\) measures the size of the decision set \(\Theta\). More concretely, assume that the loss functions \(\{f_n\}\) are convex. Then for mirror descent, with constant stepsize \(\eta\), i.e., \(\theta_{n+1} = \mathop{\mathrm{arg\,min}}_{\theta \in \Theta} f_n(\theta) + \frac{1}{\eta}D_h(\theta||\theta_n)\), where \(h\) is 1-strongly convex and \(D_h\) is the Bregman distance generated by \(h\) defined by \(D_h(x||y) = h(x) - h(y) - \langle\nabla h(y), x-y\rangle\) [41], \(R_\mathcal{A}^2\) can be set to \(\max_{x, y\in \Theta} D_h(x||y)\). And for FTRL with constant stepsize \(\eta\), i.e., \(\theta_{n+1} = \mathop{\mathrm{arg\,min}}_{\theta \in \Theta} \sum f_n(\theta) + \frac{1}{\eta} h(\theta)\), where \(h\) is 1-strongly convex and non-negative, \(R_\mathcal{A}^2\) can be set to \(\max_{\theta \in \Theta} h(\theta)\) [22].
8.2 The Generalization Error Vanishes in Expectation↩︎
The generalization error in 6 vanishes in expectation because it is a martingale difference sequence.
Lemma 2. For 1, the following holds: \(\mathbb{E}[\sum {{l}_n(\theta_n)}-\sum {{\hat{l}}_n(\theta_n)}]=0\).
Proof. We show this by working from the end of the sequence. For brevity, we use the symbol colon in the subscript to represent a set that includes the start and the end indices, e.g. \({\hat{l}}_{1:N-2}\) stands for \(\{{\hat{l}}_1, \dots, {\hat{l}}_{N-2}\}\). \[\begin{align} \mathbb{E}_{{\hat{l}}_{1:N}} \left[\sum_{t=1}^N {{l}_n(\theta_n)}\right] & = \mathbb{E}_{{\hat{l}}_{1:N-1}} \left[ \sum_{t=1}^{N-1} {{l}_n(\theta_n)}+ {l}_N(\theta_N) \right] \\ & = \mathbb{E}_{{\hat{l}}_{1:N-1}} \left[ \sum_{t=1}^{N-1} {{l}_n(\theta_n)}+ \mathbb{E}_{{\hat{l}}_N|{{\hat{l}}_{1:N-1}}} \left[ {\hat{l}}_N(\theta_N) \right] \right] \\ & =\mathbb{E}_{{\hat{l}}_{1:N-2}} \left[ \sum_{t=1}^{N-2} {{l}_n(\theta_n)}+ {l}_{N-1}(\theta_{N-1}) + \mathbb{E}_{{{\hat{l}}_{N-1:N}}|{{\hat{l}}_{1:N-2}}} \left[ {\hat{l}}_N(\theta_N) \right] \right] \\ & = \mathbb{E}_{{\hat{l}}_{1:N-2}} \left[ \sum_{t=1}^{N-2} {{l}_n(\theta_n)}+ \mathbb{E}_{{\hat{l}}_{N-1}|{{\hat{l}}_{1:N-2}}} \left[ {\hat{l}}_{N-1}(\theta_{N-1}) \right] + \mathbb{E}_{{{\hat{l}}_{N-1:N}}|{{\hat{l}}_{1:N-2}}} \left[ {\hat{l}}_N(\theta_N) \right] \right] \\ & = \mathbb{E}_{{\hat{l}}_{1:N-2}} \left[ \sum_{t=1}^{N-2} {{l}_n(\theta_n)}+\mathbb{E}_{{{\hat{l}}_{N-1:N}}|{{\hat{l}}_{1:N-2}}} \left[ \sum_{t=N-1}^N {{\hat{l}}_n(\theta_n)} \right] \right] \end{align}\] By applying the steps above repeatedly, the desired equality can be obtained. ◻
8.3 Putting Together↩︎
Finally, plugging 1 and 2 into 6 yields 8 .
9 PROOF OF THEOREM 2↩︎
9.1 Decomposition↩︎
The key to avoid the slow rate due to the direct application of martingale concentration analyses on the MDSs in 6 and 7 is to take a different decomposition of the cumulative loss. Here we construct two new MDSs in terms of the gradients: recall \({\epsilon}= \min_{\theta \in \Theta} \sum {{l}_n(\theta)}\) and let \(\theta^\star = \mathop{\mathrm{arg\,min}}_{\theta \in \Theta} \sum {{l}_n(\theta)}\). Then by convexity of \({l}_n\), we can derive \[\begin{align} \label{eq:proof32first32app} & \quad \sum {{l}_n(\theta_n)}- N {\epsilon}\nonumber \\ & \le \sum \langle{\nabla {{l}_n(\theta_n)}}, \theta_n - \theta^\star \rangle \nonumber \\ & = \sum \langle{\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}, \theta_n - \theta^\star \rangle + \sum \langle{\nabla {{\hat{l}}_n(\theta_n)}}, \theta_n - \theta^\star \rangle \nonumber \\ & \le \sum \underbrace{\langle {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}, \theta_n \rangle}_{\text{MDS}} - \sum \langle \underbrace{{\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}}_{\text{MDS}}, \theta^\star \rangle + \textrm{Regret}(\langle\nabla {\hat{l}}_n(\theta_n), \cdot\rangle) \end{align}\tag{15}\]
Our proof is based on analyzing these three terms. The two MDSs are analyzed in 9.2 and the regret is analyzed in 9.3.
9.2 Upper Bound of the Martingale Concentration↩︎
For the MDSs in 15 , we notice that, for smooth and non-negative functions, the squared norm of the gradient can be bounded by the corresponding function value through [lm:self32bounding]. This enables us to properly control the second-order statistics of the MDSs in 15 . By a recent vector-valued martingale concentration inequality that depends only on the second-order statistics [20], we obtain a self-bounding property for 15 to get a fast concentration rate. The martingale concentration inequality is stated in the following lemma.
Lemma 3 (Theorem 3 [20]). Let \(\mathcal{K}\) be a Hilbert space with norm \(\| \cdot \|\) whose dual is \(\| \cdot \| _*\). Let \(\{z_t\}\) be a \(\mathcal{K}\)-valued martingale difference sequence with respect to \(\{y_t\}\), i.e., \(\mathbb{E}_{z_t|y_1, \dots, y_{t-1}} [z_t] = 0\), and let \(h\) be a 1-strongly convex function with respect to norm \(\| \cdot \|\) and let \(B^2 = \sup_{x, y \in \mathcal{K}, \| x \| =1, \| y \| =1}D_{h}(x||y)\). Then for \(\delta \le 1/e\), with probability at least \(1-\delta\), the following holds \[\begin{align} \left \| \sum z_t \right\| _* \le 2 B\sqrt{V} + \sqrt{2 \log(1/\delta)} \sqrt{1+1/2\log(2V+2W+1)} \sqrt{2V + 2W + 1} \end{align}\] where \(V = \sum \| z_t \| _*^2\) and \(W = \sum \mathbb{E}_{z_t|y_1, \dots, y_{t-1}} \| z_t \| _*^2\).
In order to apply 3 to the MDSs in 15 , the key is to properly upper bound the statistics \(V\) and \(W\) in 3 for these MDSs.
9.2.1 Upper Bound of the Concetration for MDS \(\langle {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}, \theta_n \rangle\)↩︎
Suppose that the decision set \(\Theta\) is inside a ball centered at the origin in \(\mathcal{H}\) with radius \(R_\Theta\).
Assumption 1. There exists \(R_\Theta \in [0, \infty)\), such that \(\max_{\theta \in \Theta} \| \theta \| \le R_\Theta\).
Then by the definition of \(V\) and \(W\) in 3, and the definitions of the two problem-dependent policy class biases \({\epsilon}\) and \({\hat{\epsilon}}\) (see 1), one can obtain \[\begin{align} V & =\sum |\langle {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}, \theta_n \rangle|^2 & \nonumber \\ & \le \sum R_\Theta^2 \| {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}} \| _*^2 & \text{\ref{as:R}}\nonumber \\ & \le \sum R_\Theta^2 \left( 2 \| {\nabla {{l}_n(\theta_n)}} \| _*^2 + 2 \| {\nabla {{\hat{l}}_n(\theta_n)}} \| _*^2 \right) & \text{triangle inequality} \tag{16} \\ & \le \sum R_\Theta^2 \left( 8 \beta {{l}_n(\theta_n)}+ 8 \beta {{\hat{l}}_n(\theta_n)} \right) & \text{\ref{lm:self32bounding}}\nonumber \\ & = 8\beta R_\Theta^2 ({\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}+ N{\epsilon}+ N{\hat{\epsilon}}) & \text{\ref{def:minimum32average32loss}} \tag{17} \end{align}\] Similarly for \(W\), we have \[\begin{align} W & = \sum \mathbb{E}_{{\hat{l}}_n|\theta_n}[ |\langle {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}, \theta_n \rangle|^2] \nonumber \\ & \le\sum R_\Theta^2 \mathbb{E}_{{\hat{l}}_n|\theta_n} [\| {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}} \| _*^2] & \text{\ref{as:R}} \nonumber \\ & \le \sum R_\Theta^2 \left( 2\| {\nabla {{l}_n(\theta_n)}} \| _*^2 + 2 \mathbb{E}_{{\hat{l}}_n|\theta_n}[\| {\nabla {{\hat{l}}_n(\theta_n)}} \| _*^2] \right) & \text{triangle inequality} \tag{18} \\ & \le \sum R_\Theta^2 \left( 8 \beta {{l}_n(\theta_n)}+ 8 \mathbb{E}_{{\hat{l}}_n|\theta_n} [\beta {{\hat{l}}_n(\theta_n)}] \right) & \text{\ref{lm:self32bounding}} \nonumber \\ & = \sum R_\Theta^2 \left( 8 \beta {{l}_n(\theta_n)}+ 8 \beta {{l}_n(\theta_n)} \right) \nonumber \\ & = 16 \beta R_\Theta^2 ({\textrm{Regret}({l}_n)}+ N{\epsilon}) & \text{\ref{def:minimum32average32loss}}\tag{19} \end{align}\] Therefore, \[\begin{align} \label{eq:v95w951} V+W \le 24 \beta R_\Theta^2({\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}+ N {\epsilon}+ N {\hat{\epsilon}}) \end{align}\tag{20}\] Further suppose that the gradient of the sampled loss can be uniformly bounded:
Assumption 2. For any loss sequence \(\{{\hat{l}}_n\}\) that can be experienced by 1, suppose that there is \(G\in[0,\infty)\) such that, for any \(\theta \in \Theta\), \(\| \nabla {\hat{l}}_n(\theta) \| _* \le G\).
Then due to 20 , \(V \le 4G^2R_\Theta^2 N\) and \(W \le 4G^2 R_\Theta^2 N\). Now we are ready to invoke 3 by letting the Hilbert space \(\mathcal{K}\) in 3 be \(\mathbb{R}\), and denoting the corresponding \(B\) in 3 by \(B_\mathbb{R}\). Then, for \(\delta > 1/e\), with probability at least \(1-\delta\), the following holds \[\begin{align} \label{eq:expected32regret32for32x95t} & \quad | \sum \langle {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}, \theta_n \rangle | \nonumber \\ & \le 2B_\mathbb{R}\sqrt{8\beta R_\Theta^2}\sqrt{ {\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}+ N{\epsilon}+ N{\hat{\epsilon}}} \; + \nonumber \\ & \sqrt{96\beta R_\Theta^2 \log(1/\delta)} \sqrt{1+1/2\log(16G^2R_\Theta^2 N+1)} \sqrt{{\textrm{Regret}({l}_n)}+ N{\epsilon}+{\textrm{Regret}({\hat{l}}_n)}+ N{\hat{\epsilon}}+ 1/(48 \beta R_\Theta^2)} \end{align}\tag{21}\]
9.2.2 Upper Bound of the Concetration for MDS \({\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}\)↩︎
To bound \(\|\sum {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}\|_*\) that appears in \[\begin{align} \label{eq:x95star32cauchy} \sum \langle {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}, \theta^\star \rangle \le R_\Theta \|\sum {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}\|_* \end{align}\tag{22}\] We use 3 again in a similar way of deriving 21 , except that this time the MDS \({\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}}\) is vector-valued. Akin to showing 17 and 19 , the statistics \(V\) can be bounded as \[\begin{align} V & \le \sum \left( 2 \| {\nabla {{l}_n(\theta_n)}} \| _*^2 + 2 \| {\nabla {{\hat{l}}_n(\theta_n)}} \| _*^2 \right) \label{eq:V952} \\ & \le 8\beta ({\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}+ N{\epsilon}+ N{\hat{\epsilon}}) \end{align}\tag{23}\] and similarly for \(W\): \[\begin{align} W & \le \sum \left( 2\| {\nabla {{l}_n(\theta_n)}} \| _*^2 + 2 \mathbb{E}_{{\hat{l}}_n|\theta_n}[\| {\nabla {{\hat{l}}_n(\theta_n)}} \| _*^2] \right) \label{eq:W952} \\ & \le 16 \beta ({\textrm{Regret}({l}_n)}+ N{\epsilon}) \end{align}\tag{24}\] Therefore, \[\begin{align} \label{eq:v95w952} V+W \le 24 \beta ({\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}+ N {\epsilon}+ N {\hat{\epsilon}}) \end{align}\tag{25}\] Furthermore, by 2, it can be shown from 23 and 24 that \(V \le 4G^2 N\) and \(W \le 4G^2 N\). To invoke 3, let \(\mathcal{K}\) in 3 be \(\mathcal{H}\), and denote the corresponding \(B\) in 3 by \(B_\mathcal{H}\). Then, for \(\delta < 1/e\), with probability at least \(1-\delta\), the following holds \[\begin{align} \label{eq:expected32regret32for32x94star} & \quad \| \sum {\nabla {{l}_n(\theta_n)}}- {\nabla {{\hat{l}}_n(\theta_n)}} \| _* \nonumber \\ & \le 2B_\mathcal{H}\sqrt{8\beta}\sqrt{ {\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}+ N{\epsilon}+ N{\hat{\epsilon}}} \;+ \nonumber \\ & \quad \sqrt{96 \beta\log(1/\delta)} \sqrt{1+1/2\log(16G^2 N+1)} \sqrt{{\textrm{Regret}({l}_n)}+ N{\epsilon}+ {\textrm{Regret}({\hat{l}}_n)}+ N{\hat{\epsilon}}+ 1/(48\beta)} \end{align}\tag{26}\]
9.3 Upper Bound of the Regret↩︎
Besides analyzing the MDSs, we need to bound the regret to the linear functions defined by the gradients (the last term in 15 ). Since this last term is linear, not CSN, the bias-dependent online regret bound in the proof of [thm:rough32bound32in32expectation] does not apply. Nonetheless, because these linear functions are based on the gradients of CSN functions, we discover that their regret rate actually obeys the exact same rate as the regret to the CSN loss functions. This is notable because the regret to these linear functions upper bounds the regret to the CSN loss functions.
Lemma 4. Under the same assumptions and setup in 1, \[\begin{align} \label{eq:ol32gradient32result} \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) \le 8 \beta R_\mathcal{A}^2 + \sqrt{8\beta R_\mathcal{A}^2 N {\hat{E}}}. \end{align}\tag{27}\]
Proof. It suffices to show a self-bounding property for \(\textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle)\) as 11 . Once this is established, the rest resembles how 14 follows from 11 through algebraic manipulations. As in 1, define \(\lambda = \frac{1}{2\eta}\) and \(r^2 = 2R_\mathcal{A}^2\). Due to the property of admissible online algorithms, one can obtain \[\begin{align} \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) \le \frac{1}{\eta} R_\mathcal{A}^2 + \frac{\eta}{2}\sum \| {\nabla f_n(\theta_n)} \| _*^2 = \lambda r^2 + \sum \frac{1}{4\lambda}\| {\nabla f_n(\theta_n)} \| _*^2 \end{align}\] To proceed, as in 1, let \({\hat{\epsilon}}= \frac{1}{N}\min_{\theta \in \Theta} \sum {{\hat{l}}_n(\theta)}\) be the bias, and let \({\hat{E}}\) be such that \({\hat{E}}\geq {\hat{\epsilon}}\) almost surely. Using [lm:self32bounding] and the admissibility of online algorithm \(\mathcal{A}\) yields a self-bounding property for \(\textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle)\): \[\begin{align} \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) & \le \lambda r^2 + \frac{\beta}{\lambda} \sum f_n(\theta_n) \\ & \le \lambda r^2 + \frac{\beta}{\lambda} \textrm{Regret}(f_n) + \frac{\beta}{\lambda} N {\hat{E}}\\ & \le \lambda r^2 + \frac{\beta}{\lambda} \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) + \frac{\beta}{\lambda} N {\hat{E}} \end{align}\] This self-bounding property is exactly like what we have seen in the self-bounding property for \(\textrm{Regret}(f_n)\). After rearranging and computing the optimal \(\lambda\) (which coincides with the optimal \(\lambda\) in 1), 27 follows. ◻
4 provides a bias-dependent regret to the linear functions defined by the gradients when the (stepsize) constant \(\eta\) is set optimally in the online algorithm \(\mathcal{A}\) (used in 1). Interestingly, the optimal \(\eta\) that achieves the bias-dependent regret coincides with the one for achieving a bias-dependent regret to CSN functions. Therefore, a bias-dependent bound for \({\textrm{Regret}({\hat{l}}_n)}\) and \({\textrm{Regret}(\langle{\nabla {{\hat{l}}_n(\theta_n)}}, \cdot\rangle)}\) can be achieved simultaneously.
9.4 Putting Things Together↩︎
We now have all the pieces to prove [thm:rough32bound32in32high32probability]. Plugging 21 , 22 , and 26 into the decomposition 15 , we have, for \(\delta < 1/e\), with probability at least \(1-2\delta\) \[\begin{align} & \quad {\textrm{Regret}({l}_n)}\\ & \le 2B_\mathbb{R}\sqrt{8\beta R_\Theta^2}\sqrt{ {\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}+ N{\epsilon}+ N{\hat{\epsilon}}} \\ & +\sqrt{96\beta R_\Theta^2 \log(1/\delta)} \sqrt{1+1/2\log(16G^2R_\Theta^2 N+1)} \sqrt{{\textrm{Regret}({l}_n)}+ N{\epsilon}+{\textrm{Regret}({\hat{l}}_n)}+ N{\hat{\epsilon}}+ 1/(48 \beta R_\Theta^2)} \\ & + 2B_\mathcal{H}\sqrt{8\beta R_\Theta^2}\sqrt{ {\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}+ N{\epsilon}+ N{\hat{\epsilon}}} \\ & + \sqrt{96 \beta\log(1/\delta)} \sqrt{1+1/2\log(16G^2 N+1)} \sqrt{{\textrm{Regret}({l}_n)}+ N{\epsilon}+ {\textrm{Regret}({\hat{l}}_n)}+ N{\hat{\epsilon}}+ 1/(48 \beta)} \\ & + \textrm{Regret}(\langle\nabla {\hat{l}}_n(\theta_n), \cdot\rangle) \end{align}\] To simplify it, we denote \[\begin{align} A_1 & = 8 \max(B_\mathbb{R}, B_\mathcal{H}) \sqrt{2 \beta R_\Theta^2}, \\ A_2 & = 8\sqrt{6 \beta R_\Theta^2 \log(1/\delta)} \sqrt{1 +1/2 \log(16G^2\max(1, R_\Theta^2)N+1)}, \\ \tilde{R} & = \min(1, R_\Theta) \end{align}\] Plugging them into the above upper bound on \({\textrm{Regret}({l}_n)}\) and using the basic inequality \(\sqrt{a+b} \le \sqrt{a}+\sqrt{b}\) yield \[\begin{align} {\textrm{Regret}({l}_n)} & \le (A_1 + A_2) \sqrt{{\textrm{Regret}({l}_n)}+ {\textrm{Regret}({\hat{l}}_n)}} + (A_1+A_2) \sqrt{ N{\epsilon}+ N{\hat{\epsilon}}} \\ & + \frac{A_2}{\sqrt{48 \beta \tilde{R}^2}} + \textrm{Regret}(\langle\nabla {\hat{l}}_n(\theta_n), \cdot\rangle) \end{align}\] To further simplify, using the basic inequality \(\sqrt{ab} \le (a+b)/2\) yields \[\begin{align} {\textrm{Regret}({l}_n)}& \le \frac{{\textrm{Regret}({l}_n)}}{2} + \frac{{\textrm{Regret}({\hat{l}}_n)}}{2} +(A_1 + A_2) \sqrt{ N{\epsilon}+ N{\hat{\epsilon}}} \\ & + \frac{(A_1 + A_2)^2}{2} + \frac{A_2}{\sqrt{48 \beta \tilde{R}^2}} + \textrm{Regret}(\langle\nabla {\hat{l}}_n(\theta_n), \cdot\rangle) \end{align}\] Rearranging terms and invoking the bias-dependent rate in 1 and 4 give \[\begin{align} \label{eq:plug32in32bias-dependent32rate} {\textrm{Regret}({l}_n)}& \le {\textrm{Regret}({\hat{l}}_n)}+2(A_1 + A_2)\sqrt{ N{\epsilon}+ N{\hat{\epsilon}}}+ (A_1+A_2)^2 + \frac{A_2}{\sqrt{12 \beta \tilde{R}^2}} + 2\textrm{Regret}(\langle\nabla {\hat{l}}_n(\theta_n), \cdot\rangle) \nonumber \\ & \le 2(A_1 + A_2)\sqrt{ N{\epsilon}+ N{\hat{\epsilon}}} + 6\sqrt{2\beta R_\mathcal{A}^2 N {\hat{E}}} + (A_1+A_2)^2 + \frac{A_2}{\sqrt{12 \beta \tilde{R}^2}} + 24 \beta R_\mathcal{A}^2 \end{align}\tag{28}\] Finally, to derive a big-\(O\) bound, denote \[\begin{align} R = \max(1, R_\Theta, R_\mathcal{A}), \quad C = \log(1/\delta) \log(G R N) \end{align}\] then one can obtain the rate in terms of \(N\) in big-\(O\) notation, while keeping \(\tilde{R}\), \(R\), \(B_\mathbb{R}\), \(B_\mathcal{H}\), \(\log(1/\delta)\), \(G\), \({\epsilon}\), and \({\hat{E}}\) as multipliers: \[\begin{align} {\textrm{Regret}({l}_n)}= O \left( C \beta R^2 + \sqrt{C \beta R^2 N({\hat{E}}+ {\epsilon})} \right) \end{align}\] Therefore \[\begin{align} \frac{1}{N}\sum {{l}_n(\theta_n)}- {\epsilon}= O \left( \frac{C \beta R^2}{N} + \sqrt{\frac{C \beta R^2 ({\hat{E}}+ {\epsilon})}{N}} \right) \end{align}\]
In 8 and 9, we proved new bias-dependent rates in expectation ([thm:rough32bound32in32expectation]) and in high-probability ([thm:rough32bound32in32high32probability]). However, these rates hold only provided that the stepsize of the online algorithm \(\mathcal{A}\) in 1 is constant and properly tuned; this requires knowing in advance the smoothness factor \(\beta\), an upper bound of the bias \(\hat{\epsilon}\), and the number of rounds \(N\). Therefore, these theorems are not directly applicable to practical online IL algorithms that update the stepsize adaptively without knowing the constants beforehand.
Fortunately, [thm:rough32bound32in32expectation] and [thm:rough32bound32in32high32probability] can be adapted to online IL algorithms that utilize online algorithms with adaptive stepsizes in a straightforward manner, which we shall show next. The key insight is that online algorithms with adaptive stepsizes obtain almost the same guarantee as they would have known the optimal constant stepsize in advance. For example, [19] shows that for Online Subgradient Descent [42], the difference between the guarantees of using the optimal constant stepsize and the guarantee of using adaptive stepsizes \(\eta_n = \frac{\sqrt{2}D}{2 \sqrt {\sum_{i=1}^n \|g_i\|_2^2}}\) is only a factor of \(\sqrt{2}\).
Lemma 5 (Theorem 4.14 [19]). Let \(V \subseteq \mathbb{R}^d\) a closed non-empty convex set with diameter \(D\), i.e., \(\max_{x, y \in V} \|x -y\|_2 \le D\). Let \(f_1, \dots, f_N\) be an arbitrary sequence of non-negative convex functions \(f_n: \mathbb{R}^d \to (-\infty, +\infty]\) differentiable in open sets containing \(V\) for \(t=1, \dots, T\). Pick any \(x_1 \in V\) and stepsize \(\eta_n = \frac{\sqrt{2}D}{2 \sqrt {\sum_{i=1}^n \|\nabla f_i(x_i\|_2^2}}\), \(n = 1, \dots, N\). Then the following regret bound holds for online subgradient descent: \[\begin{align} \label{eq:adaptive32online32algorithm} \mathrm{Regret}(f_n) \le \sqrt{2} \min_{\eta>0} \left( \frac{D^2}{2\eta} + \frac{\eta}{2} \sum_{n=1}^T \|\nabla f_n(x_n)\|_2^2 \right) \end{align}\tag{29}\]
Inspired by this insight, we propose a more general definition of admissible online algorithms (cf. 2) and a notion of proper stepsizes:
Definition 4 (General admissible online algorithm). We say an online algorithm \(\mathcal{A}\) is admissible on a parameter space \(\Theta\), if there exists \(R_\mathcal{A}\in[0,\infty)\) such that given any sequence of differentiable convex functions \(f_n\) and stepsizes \(\eta_n\), \(\mathcal{A}\) can achieve \(\textrm{Regret}(f_n) \le \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) \le \frac{1}{\eta} R_\mathcal{A}^2 + \frac{1}{2}\sum \eta_n \| {\nabla f_n(\theta_n)} \| _*^2\), where \(\theta_n\) is the decision made by \(\mathcal{A}\) in round \(n\).
The admissible online algorithms that we discussed in the last paragraph of 8.1 also belong to this category of genearal admissible algorithms.
Definition 5 (Proper stepsizes). A stepsize adaptation rule is proper if there exists \(K \in (0, \infty)\) such that for any admissible online algorithm \(\mathcal{A}\) (4) with the stepsize \(\eta_n\) chosen according to the rule based on the information till round \(n\) can achieve \(\textrm{Regret}(f_n) \le \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) \le K \min_{\eta > 0} \left( \frac{1}{\eta} R_\mathcal{A}^2 + \frac{1}{2}\sum \eta \| {\nabla f_n(\theta_n)} \| _*^2 \right)\).
With the general definition of admissible online algorithms (4) and the definition of proper stepsizes (5), we can now extend the bias-dependent regret (1) which assumes optimal constant stepsize to adaptive online algorithms with proper stepsizes. This lemma will be the foundation of extending [thm:rough32bound32in32expectation] and [thm:rough32bound32in32high32probability].
Lemma 6. Consider running an admissible online algorithm \(\mathcal{A}\) on a sequence of CSN loss functions \(\{f_n\}\) with adaptive stepsizes that are proper. Let \(\{\theta_n\}\) denote the online decisions made in each round, and let \({\hat{\epsilon}}= \frac{1}{N}\min_{\theta \in \Theta} \sum f_n(\theta)\) be the bias, and let \({\hat{E}}\) be such that \({\hat{E}}\geq {\hat{\epsilon}}\) almost surely. Then the following holds \[\begin{align} \textrm{Regret}(f_n) \le 8 K^2 \beta R_\mathcal{A}^2 + \sqrt{8 K^2\beta R_\mathcal{A}^2 N {\hat{E}}}. \end{align}\]
Proof. Because the online algorithm \(\mathcal{A}\) is admissible and the stepsizes are proper, we have, for any \(\eta > 0\) \[\begin{align} \label{eq:adaptive32constant32stepsize} \textrm{Regret}(f_n) \le \frac{K}{\eta} R_\mathcal{A}^2 + \frac{K \eta}{2}\sum \| {\nabla f_n(\theta_n)} \| _*^2 \end{align}\tag{30}\] Let \(\lambda = \frac{1}{2\eta}\) and \(r^2 = 2R_\mathcal{A}^2\), then \[\begin{align} \frac{K}{\eta} R_\mathcal{A}^2 + \frac{K \eta}{2}\sum \| {\nabla f_n(\theta_n)} \| _*^2 = K \lambda r^2 + \sum \frac{K}{4\lambda}\| {\nabla f_n(\theta_n)} \| _*^2 \end{align}\] Using [lm:self32bounding] yields a self-bounding property for \(\textrm{Regret}(f_n)\): \[\begin{align} \label{eq:adaptive32concrete32self-bounding} \textrm{Regret}(f_n) \le K \lambda r^2 + \frac{K\beta}{\lambda} \sum f_n(\theta_n) \le K\lambda r^2 + \frac{K\beta}{\lambda} \textrm{Regret}(f_n) + \frac{K\beta}{\lambda} N {\hat{E}} \end{align}\tag{31}\] Let \(\hat{\beta} = K\beta\) and \(\hat{r}^2 =K r^2\), and by rearranging the terms, we have a bias-dependent upper bound (cf. 12 ) that for any \(\eta> 0\), \[\begin{align} \label{eq:adaptive32proof32thm132bound} \textrm{Regret}(f_n) \le \frac{\hat{\beta}}{\lambda - \hat{\beta}} N{\hat{E}}+ \frac{\lambda^2}{\lambda - \hat{\beta}} \hat{r}^2 \end{align}\tag{32}\] The upper bound can be minimized by choosing an optimal \(\lambda\). Setting the derivative of the right-hand side to zero, and computing the optimal \(\lambda\) (\(\lambda > 0\)) gives us \[\begin{align} \label{eq:adaptive32lambda} \hat{r}^2 \lambda^2 - 2 \hat{\beta} \hat{r}^2 \lambda - \hat{\beta} N {\hat{E}}= 0, \quad \lambda > 0 \quad \text{ and } \quad \lambda = \hat{\beta} + \sqrt{\hat{\beta}^2 + \frac{\hat{\beta} N {\hat{E}}}{\hat{r}^2}} \end{align}\tag{33}\] which implies that the optimal \(\eta\) is \(\frac{1}{2 \left( \hat{\beta} + \sqrt{\hat{\beta}^2 + \frac{\hat{\beta} N {\hat{E}}}{2 R_\mathcal{A}^2}} \right) }\). Because 32 holds for any \(\eta\), it holds for the optimal \(\eta\) too. Next, we simplify 32 . Since the optimal \(\lambda\) satisfies the equality \(\hat{\beta} N {\hat{E}}= \hat{r}^2 \lambda^2 - 2 \hat{\beta} \hat{r}^2 \lambda\) implied from 33 , 32 can be written as \[\begin{align} \textrm{Regret}(f_n) & \le \frac{1}{\lambda-\hat{\beta}} \hat{\beta} N {\hat{E}}+ \frac{\lambda^2}{\lambda - \hat{\beta}} \hat{r}^2 = \frac{1}{\lambda - \hat{\beta}}(\hat{r}^2 \lambda^2 - 2 \hat{\beta} \hat{r}^2 \lambda) +\frac{\lambda^2}{\lambda - \hat{\beta}} \hat{r}^2 \nonumber \\ & =\frac{2\lambda^2 \hat{r}^2 - 2\hat{\beta} \lambda \hat{r}^2}{\lambda - \hat{\beta}} = 2 \lambda \hat{r}^2 \end{align}\] Plugging in the optimal \(\lambda\) yields \[\begin{align} \label{eq:adaptive32ol32result} \textrm{Regret}(f_n) & \le 2 \lambda \hat{r}^2 = 2 \left( \hat{\beta} + \sqrt{\hat{\beta}^2 + \frac{\hat{\beta} N{\hat{E}}}{\hat{r}^2}} \right) \hat{r}^2\nonumber \\ & = 2 \hat{\beta} \hat{r}^2 + \sqrt{2\hat{\beta} \hat{r}^2} \sqrt{2\hat{\beta} \hat{r}^2 + 2N{\hat{E}}} \nonumber \\ & \le 4 \hat{\beta} \hat{r}^2 + 2 \sqrt{\hat{\beta} \hat{r}^2 N {\hat{E}}} \nonumber \\ & = 8 K^2 \beta R_\mathcal{A}^2 + \sqrt{8K^2 \beta R_\mathcal{A}^2 N {\hat{E}}} \end{align}\tag{34}\] where the last inequality uses the basic inequality: \(\sqrt{a+b}\leq\sqrt{a}+\sqrt{b}\). ◻
Provided the bias-dependent regret 6 (cf. 1), a bias-dependent rate in expectation for online IL with an additional constant \(K\) due to the adaptive stepsizes (cf. [thm:rough32bound32in32expectation]) follows directly, because 2 still holds even if the stepsizes of the online algorithm in 1 become adaptive. In order to extend [thm:rough32bound32in32high32probability] to admissible online algorithm with adaptive stepsizes, we first need to derive a bias-dependent regret to the linear functions defined by the gradients (cf. 4) based on the proof of 6.
Lemma 7. Under the same assumptions and setup in 6, \[\begin{align} \label{eq:adaptive32ol32gradient32result} \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) \le 8 K^2 \beta R_\mathcal{A}^2 + \sqrt{8K^2 \beta R_\mathcal{A}^2 N {\hat{E}}}. \end{align}\tag{35}\]
Proof. It suffices to show a self-bounding property for \(\textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle)\) as 31 . Once this is established, the rest resembles how 34 follows from 31 through algebraic manipulations. As in 6, define \(\lambda = \frac{1}{2\eta}\) and \(r^2 = 2R_\mathcal{A}^2\). Due to the property of admissible online algorithms, one can obtain, for any \(\eta\) \[\begin{align} \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) \le \frac{K}{\eta} R_\mathcal{A}^2 + \frac{K\eta}{2}\sum \| {\nabla f_n(\theta_n)} \| _*^2 = K \lambda r^2 + \sum \frac{K}{4\lambda}\| {\nabla f_n(\theta_n)} \| _*^2 \end{align}\] To proceed, as in 1, let \({\hat{\epsilon}}= \frac{1}{N}\min_{\theta \in \Theta} \sum {{\hat{l}}_n(\theta)}\) be the bias, and let \({\hat{E}}\) be such that \({\hat{E}}\geq {\hat{\epsilon}}\) almost surely. Using [lm:self32bounding] and the admissibility of online algorithm \(\mathcal{A}\) yields a self-bounding property for \(\textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle)\): \[\begin{align} \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) & \le K \lambda r^2 + \frac{K \beta}{\lambda} \sum f_n(\theta_n) \\ & \le K \lambda r^2 + \frac{K\beta}{\lambda} \textrm{Regret}(f_n) + \frac{K\beta}{\lambda} N {\hat{E}}\\ & \le K\lambda r^2 + \frac{K\beta}{\lambda} \textrm{Regret}(\langle{\nabla f_n(\theta_n)}, \cdot\rangle) + \frac{K\beta}{\lambda} N {\hat{E}} \end{align}\] This self-bounding property is exactly like what we have seen in the self-bounding property for \(\textrm{Regret}(f_n)\). After rearranging and computing the optimal \(\lambda\) (which coincides with the optimal \(\lambda\) in 1), 35 follows. ◻
Given the bias-dependent rates in online learning (6 and 7), a high-probability bias-dependent rate for online IL with an additional constant \(K\) due to adaptive stepsizes (cf. [thm:rough32bound32in32high32probability]) can the derived in the same way as the proof of [thm:rough32bound32in32high32probability], except that 6 and 7 will be invoked in 28 in place of 1 and 4.
Interestingly, [19] provides a bias-dependent regret for Online Subgradient Descent with adaptive stepsizes \(\eta_n = \frac{\sqrt{2}D}{2 \sqrt {\sum_{i=1}^n \|g_i\|_2^2}}\) (cf. 6). Although that regret bound would help more directly prove [thm:rough32bound32in32expectation] in the adaptive stepsize setting, but it does not directly imply a bias-dependent regret to the linear functions defined by the gradients (cf. 7)
10 EXPERIMENT DETAILS↩︎
Although the main focus of this paper is the new theoretical insights, we conduct experiments to provide evidence that the fast policy improvement phenomena indeed exist, as our theory predicts. We verify the change of the policy improvement rate due to policy class capacity by running an online IL experiment in the CartPole balancing task in OpenAI Gym [43] with DART physics engine [44].
10.1 MDP Setup↩︎
The goal of the CartPole balancing task is to keep the pole upright by controlling the acceleration of the cart. This MDP has a 4-dimensional continuous state space (the position and the velocity of the cart and the pole), and 1-dimensional continuous action space (the acceleration of the cart). The initial state is a configuration with a small uniformly sampled offset from being static and vertical, and the dynamics is deterministic. This task has a maximum horizon of \(1000\). In each time step, if the pole is maintained within a threshold from being upright, the learner receives an instantaneous reward of one; otherwise, the learner receives zero reward and the episode terminates. Therefore, the maximum sum of rewards for an episode is \(1000\).
10.2 Expert Policy Representation and Training↩︎
To simulate the online IL task, we consider a neural network expert policy (with one hidden layer of \(64\) units and \(\mathrm{tanh}\) activation), and the inputs to the neural network is normalized using a moving average over the samples. The expert policy is trained using a model-free policy gradient method (ADAM [40] with GAE [39]). And the value function used by GAE is represented by a neural network with two hidden layers of \(128\) units and \(\mathrm{tanh}\) activation. To compute the policy gradient during training, additional Gaussian noise (with zero mean and a learnable variance that does not depend on the state) is added to the actions, and the gradient is computed through log likelihood ratio. After \(100\) rounds of training, the expert policy can consistently achieve the maximum sum of rewards both with and without the additional Gaussian noise. After the expert policy is trained, during online IL, Gaussian noise is not added in order to reduce the variance in the experiments.
10.3 Learner Policy Representation↩︎
We let the learner policy be another neural network that has exactly the same architecture as the expert policy with no Gaussian noise added.
10.4 Online IL Setup↩︎
10.4.0.1 Policy class
We conduct online IL with unbiased and biased policy classes. One one hand, we define the unbiased class as all the policies satisfying the representation in 10.3. On the other hand, we define the biased policy classes by imposing an additional \(\ell_2\)-norm constraint on the learner’s weights in the output layer so that the learner cannot perfectly mimic the expert policy. More concretely, in the experiments, the \(\ell_2\)-norm constraint has sizes \(\{0.1, 0.12, 0.15\}\).
10.4.0.2 Loss functions
We select \({{l}_n(\theta)}= \mathbb{E}_{s \sim d_{\pi_{\theta_n}}} [H_\mu(\pi_\theta(s) - {\pi_\mathrm{e}}(s))]\) as the online IL loss (see 2.2), where \(H_\mu\) is the Huber function defined as \(H_\mu(x) = \frac{1}{2} x^2\) for \(| x | \le \mu\) and \(\mu | x | - \frac{1}{2}\mu^2\) for \(| x | > \mu\). In the experiments, \(\mu\) is set to \(0.05\); as a result, \(H_\mu\) is linear when its function value is larger than \(0.00125\). Because the learner’s policy is linear, this online loss is CSN in the unknown weights of the learner.
10.4.0.3 Policy update rule
We choose AdaGrad [45], [46] as the online algorithm in 1; AdaGrad is a first-order mirror descent algorithm , When the \(\ell_2\)-norm constraint is imposed, an additional projection step is taken after taking a gradient step using AdaGrad. The final algorithm is a special case of the DAgger algorithm [1] (called DAggereD in [24]) with only first-order information and continuous actions [24]. In the experiments, the stepsize is set to \(0.01\). In each round, for updating the learner policy, \(1000\) samples, i.e., state and expert action pairs, are gathered, and for computing the loss \({l}_n(\theta_n)\), more samples (\(5000\) samples) are used due to the randomness in the initial state of the MDP.
10.4.0.4 Hyperparameter tuning
The hyperparameters are tuned in a very coarse manner. We eliminated the ones that are obviously not proper. Here are the hyperparameters we have tried. The stepsize in online IL: \(0.1, 0.01, 0.001\). The Huber function parameter \(\mu\): \(0.05\).
References↩︎
The online decision in the iterative process of online learning should not be confused with the decisions made at each time step in sequential decision making.↩︎
A function \(f\) is \(\beta\)-smooth if its gradient \(\| \nabla f(x) - \nabla f(y) \| _* \leq \beta \| x-y \|\) for \(x,y\in\mathcal{X}\).↩︎
The i.i.d. concentration lemma further depends on a martingale concentration bound [30], which relies on an almost-surely upper bound of the second-order statistics. In comparison, the martingale concentration we utilize in this work relies on second-order statistics that are defined on the sample path [20].↩︎